Abstract
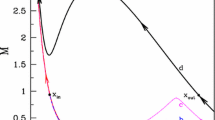
We present the analytic theory of dissipative and non-dissi-pative shocks in the rotating outflows in both the pseudo-Newtonian and the Schwarzschild geometry. We include the effects of the self gravity of the surrounding massive disc and show that the flow may have as many as five critical points when the angular momentum and the disc mass are sufficiently high. This leads to the possibility of the multipleannular shocks within the flow. We derive the expressions correlating the pre-shock and the post-shock quantities for all the three principal types of discontinuities. From these relations it is shown that for given initial flow parameters such as the angular momentum and the energy there could be as many as eighteen formal shock locations out of which at most two are chosen in reality. Detailed classification of the parameter space in terms of the initial flow parameters will be discussed elsewhere
Similar content being viewed by others
References
Abramowicz, M. A., Chakrabarti, S. K. 1989,Astrophys. J., (submitted).
Abramowicz, M. A., Zurek, W. H. 1981,Astrophys. J.,246, 314.
Anderson, M. 1989,Mon. Not. R. astr. Soc, (in press).
Begelman, M., Blandford, R., Rees, M. J. 1984,Rev. mod. Phys.,56, 255.
Chakrabarti, S. K. 1986,Astrophys: J.,303, 582.
Chakrabarti, S. K. 1988,J. Astrophys. Astr.,9, 49.
Chakrabarti, S. K. 1989a,Publ. astr. Soc. Japan, (C1, in press).
Chakrabarti, S. K. 1989b,Astrophys. J.,337, L89 (C2).
Chakrabarti, S. K. 1989c,Mon. Not. R. astr. Soc, (in press).
Chakrabarti, S. K. 1989d,Astrophys. J., (in press).
Chakrabarti, S. K. 1989e,Mon. Not. R. astr. Soc, (submitted).
Chandrasekhar, S. 1983,Mathematical Theory Of Black Holes, Cambridge Univ. Press.
Chang, K. M., Ostriker, J. P. 1985,Astrophys. J.,288, 428.
Ferrari, A., Trussoni, E., Rosner, R., Tsinganos K. 1985,Astrophys. J.,294, 397.
Fukue, J. 1982,Publ. astr. Soc. Japan,34, 163.
Fukue, J. 1987,Publ. astr. Soc. Japan,39, 309.
Holzer, T. E. 1977,J. geophys. Res.,82, 23.
Landau, L. D., Lifshitz, F. D. 1959,Fluid Dynamics, Pergamon Press, New York.
Liang, E. P. T., Thompson, K. A. 1980,Astrophys. J.,240, 271.
Paczynski, B., Wiita, P. J. 1980,Astr. Astrophys.,88, 23.
Parker, E. N. 1963,Interplanetary Dynamical Processes, Interscience, New York.
Poston, T., Stewart, I. 1978,Catastrophe Theory and its Applications, Pitman, London.
Pudritz, R. E., Norman, C. A. 1983,Astrophys. J.,274, 677.
Silvestro, G. Ferrari, A., Rosner, R., Trussoni, E., Tsinganos, K. 1987,Nature,325, 228.
Uchida, Y., Kaifu, N., Shibata, K., Hayashi, S. S., Hasegawa, T., Hamatake, H. 1988,Publ. astr. Soc. Japan,39, 907.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Chakrabarti, S.K. Multiple shocks in the rotating winds from self-gravitating discs. J. Astrophys. Astr. 10, 261–277 (1989). https://doi.org/10.1007/BF02715000
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF02715000