Summary
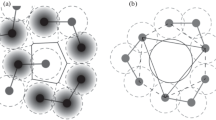
A simple model for the structure of monoatomic liquids, related to a previous one of Prins and Petersen, is described and the formulae for the radial density, the time-dependent radial density and the scattering function are worked out.
Riassunto
Si discute un modello semplice, valido per la struttura dei liquidi monoatomici e connesso con una precedente ipotesi dovuta a Prins e Petersen. Precisato il modello, se ne deducono delle formule approssimate per la densità radiale, la densità radiale dipendente dal tempo e per la funzione di scattering.
Реэюме
Описывается простая модель для структуры моноатомных жидкостей, свяэанная с предыдушей моделью Принса и Петерсена, и выводятся формулы для радиальной плотности, для радиальной плотности, эависяшей от времени, и для функции рассеяния.
Article PDF
Similar content being viewed by others
References
This model, in its essential lines, was arrived at during some previous work on the structure of liquid4He. (S. Franchetti:Nuovo Cimento,22, 374 (1961).) We describe it here in a more detailed way and for a nonquantum liquid.
J. A. Prins andH. Petersen:Physica,3, 147 (1936).
R. Kaplow, S. L. Strong andB. L. Averbach:Phys. Rev.,138, A 1336 (1965);R. R. Fessler, R. Kaplow andB. L. Averbach:Phys. Rev.,150, 34 (1966).
J. Frenkel:Kinetic Theory of Liquids (Oxford, 1946), p. 114.
G. Fournet:Enc. of Phys.,32, 244 (1957).
G. H. Vineyard: inLiquid Metals and Solidification (published by the American Society of Metals), p. 30. The author is indebted toG. H. Vineyard for kindly supplying him with a reproduction of this article.
F. Zernike andJ. A. Prins:Zeits. f. Phys.,41, 184 (1927).
In principle, neutrons should of course be treated differently, as the fundamental work ofVan Hove and others has shown. When however it comes to the practical job of deducing the radial density from the scattering data, it is the Zernike and Prins equation, valid for X-rays, that is mostly employed. That one can improve somewhat upon this procedure has been shown only recently byP. Ascarelli andG. Caglioti:Nuovo Cimento,43 B, 375 (1966).
In particular, formula 26, p. 74, vol.1 ofA. Erdelyi,et al.: Tables of Integral Transforms (New York, 1954). In this formula the value of the Erfc is indistinguishable from 2.0. (SeeM. Abramovitz andI. Stegun:Handbook of Mathematical Functions, formula 7.1.29 (New York, 1965), p. 299.)
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Franchetti, S. On a model for monoatomic liquids. Nuovo Cimento B (1965-1970) 55, 335–347 (1968). https://doi.org/10.1007/BF02711646
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/BF02711646