Abstract
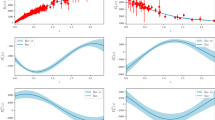
The classical stochastic model of cosmology recently developed by us is reconsidered. In that approach the parameterw defined by the equation of statep = wp was taken to be fluctuating with mean zero and we compared the theoretical probability distribution function (PDF) for the Hubble parameter with observational data corresponding to a universe with matter and vacuum energy. Even though qualitative agreement between the two was obtained, an attempt is herein made to introduce a more realistic assumption for the mean ofw and use it for the calculations. In the present theory the mean values of bothp andw are taken to be nonzero. The theoretical and observational PDFs are compared for different epochs and values of the Hubble parameter. The corresponding values of the diffusion constantD obtained are approximately constant. We use the scatter in the observed redshift-magnitude data of Type Ia supernova to place limits on the stochastic variation in expansion rate and consequently, on the stochastic variation of the equation of state.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
C Sivakumar, M V John and K Babu Joseph,Pramana - J. Phys. 56, 477 (2001)
C Sivakumar, M V John and K Babu Joseph, Revised version submitted toInt. J. Mod. Phys. D (2001)
S Perlmutteret al, Astrophys. J. 517, 565 (1999)
A G Riesset al, Astron. J. 116, 1009 (1998)
W L Freedmanet al, Nature 371, 757 (1994)
M J Pierce, D L Welch, R D McClure, S. van den Bergh, R Racine and P B Stetson,Nature 371, 385 (1994)
I Zehavi and A Dekel,Nature 401, 252 (1999)
L M Krauss,Astrophys. J. 501, 461 (1998)
M Kamionkowski and N Toumbas,Phys. Rev. Lett. 77, 587 (1996)
R R Caldwell, R Dave and P J Steinhardt,Phys. Rev. Lett. 80, 1582 (1998)
I Zlatev, L Wang and P J Steinhardt,Phys. Rev. Lett. 82, 896 (1999)
H Risken,The Fokker-Planck equation (Springer-Verlag, New York, 1984)
T Padmanabhan, To appear in the proceedings of XIII Rencontres de Blois-Frontiers of the universe, June 17–23 (2001), gr-qc/0112068
M V John and K Babu Joseph,Phys. Rev. D61, 087304 (2000)
M V John and J V Narlikar,Phys. Rev. D65, 043506 (2002)
J Weller and A Albrecht, astro-ph/0106079
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
John, M.V., Sivakumar, C. & Joseph, K.B. Classical stochastic approach to cosmology revisited. Pramana - J Phys 60, 1–10 (2003). https://doi.org/10.1007/BF02705063
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02705063