Abstract
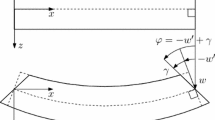
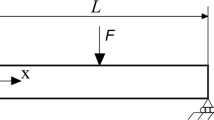
Despite satisfying only completeness and continuity requirements, elements often perform erroneously in a certain class of problems, called the locking situations, where they display spurious stress oscillations and enhanced stiffness properties. The function space approach that effectively substantiates the postulates of the field consistency paradigm is an efficient tool to reveal the fundamental cause of locking phenomena, and propose methods to eliminate this pathological problem. In this paper, we review the delayed convergence behaviour of three-noded Timoshenko beam elements using the rigorous function space approach. Explicit, closed form algebraic results for the element strains, stresses and errors have been derived using this method. The performance of the field-inconsistent three-noded Timoshenko beam element is compared with that of the field-inconsistent two-noded beam element. It is demonstrated that while the field-inconsistent two-noded linear element is prone to shear locking, the field-inconsistent three-noded element is not very vulnerable to this pathological problem, despite the resulting shear oscillations.
Similar content being viewed by others
References
Carpenter N, Belytschko T, Stolarski H 1986 Locking and shear scaling factors in C0 bending elements.Comput. Struct. 22: 39–52
Edwards L H, Penny D E 1988Elementary linear algebra (Englewood Cliffs, NJ: Prentice-Hall)
Mukherjee S, Prathap G 2001 Analysis of shear locking in Timoshenko beam elements using the function space approach.Commun. Numer. Methods Eng. 17: 385–393
Prathap G 1982 Reduced integration and the shear flexible beam element.Int. J. Numer. Methods Eng. 18: 195–210
Prathap G 1987 Field-consistency and violent stress oscillations in the finite element method.Int. J. Numer. Methods Eng. 24: 2017–2033
Prathap G 1993The finite element method in structural mechanics (Dordrecht: Kluwer Academic)
Tessler A, Hughes T J R 1983 An improved treatment of transverse shear in the Mindlin type fournode quadrilateral element.Comput. Methods Appl. Mech. Eng. 39: 311–335
Zienkiewicz O C, Taylor R L 1991The finite element method (New York: McGraw-Hill)
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Mukherjee, S., Prathap, G. Analysis of delayed convergence in the three-noded Timoshenko beam element using the function space approach. Sadhana 27, 507–526 (2002). https://doi.org/10.1007/BF02703292
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02703292