A Map for a Group of Resonant Cases in a quartic Galactic Hamiltonian

Abstract

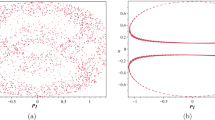
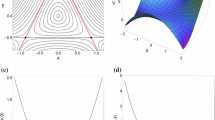
We present a map for the study of resonant motion in a potential made up of two harmonic oscillators with quartic perturbing terms. This potential can be considered to describe motion in the central parts of non-rotating elliptical galaxies. The map is based on the averaged Hamiltonian. Adding on a semi-empirical basis suitable terms in the unperturbed averaged Hamiltonian, corresponding to the 1:1 resonant case, we are able to construct a map describing motion in several resonant cases. The map is used in order to find thex − p _x Poincare phase plane for each resonance. Comparing the results of the map, with those obtained by numerical integration of the equation of motion, we observe, that the map describes satisfactorily the broad features of orbits in all studied cases for regular motion. There are cases where the map describes satisfactorily the properties of the chaotic orbits as well.