Abstract
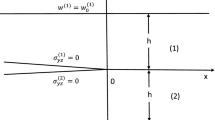
The transient response of a central crack in an orthotropic strip under the in-plane shear impact loading is studied by using the dual integral equation method proposed by Copson and Sih. The general formula for the shear stress intensity factor\(\tilde K_{II} (t)\) near the crack tip is derived. Numerical results of\(\tilde K_{II} (T)\) with\(T \equiv \frac{{c_s t}}{a}\) in various cases are obtained by solving the second kind Fredholm integral equation and by performing the inverse Laplace transform.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Sih GC, Chen EP. Mechanics of fracture 6: cracks in composite materials. Hague: Martinus Nijhoff Publishers, 1981
Kassir MK, Bandyopadhyay KK. Impact response of a cracked orthotropic medium.J Appli Mechanics, 1983, 50: 630–636
Shindo Y et al. Impact response of a finite crack in an orthotropic strip.Acta Mechanics, 1986, 62: 87–104
Shindo Y et al. Impact response of a single edge crack in an orthotropic strip.J Appli Mechanics, 1992, 59: S152-S157
Copson ET. On certain dual integral equations. Proc Glasgow Math Association, 1961, 5: 21–24
Miller MK, Guy WT. Numerical inversion of the Laplace transform by use of Jacobi polynomials.SIAM Journal of Numerical Analysis, 1966, 3: 624–635
Watson GN. A treatise on the theory of Bessel functions. Second edition. Cambridge: Cambridge University Press, 1985
Gradshteyn IS, Ryzhik IM. Table of Integrals, Series and Products. New York: London Academic Press, 1980
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Xiaolu, X., Yijun, H. Transient response of a finite crack in an orthotropic strip under the in-plane shear impact. Acta Mech Sinica 11, 349–356 (1995). https://doi.org/10.1007/BF02488842
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02488842