Skip to main content
SpringerLink
Log in

Variational principle of hybrid energy and the fundamentals of 3-D laminate theory—A new approach for the analysis of interlaminar stresses in composite laminates

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

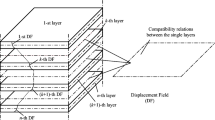
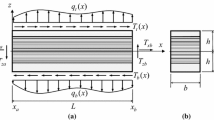
This paper discusses the discontinuity of stresses and strains at interlaminar surfaces of the composue laminate and presents a 3-D laminate theory for composite materials. This paper also presents a new type of elastic energy based on the globally continuous variables in laminates, different from the traditional potential energy and complementary energy. Then, a variational principle corresponding to the 3-D laminate theory is developed. The theory and the principle could be a basis of verifying the 2-D laminate theory and determining the interlaminar stresses near the free edges.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Lekhnitskii, S.G.,Theory of Elasticity of an Anisotropic Body, Gostekhizdat, Moscow (1950). (in Russian). Transl., Holden-Day, San Francisco (1963). Second Edition, Nauka, Moscow, (1977), (in Russian). Transl., Mir Publishers, Moscow (1981).

    MATH  Google Scholar 

  2. Pipes, R.B.,J. Compos. Mater.,4, Oct (1970), 538–548.

    Google Scholar 

  3. Altus, E., A. Rotem, and M. Shmueli,J. Compos. Mater.,14 (1980), 21–30.

    Google Scholar 

  4. Engblom, J.J. and O.O. Ochoa,Int. J. Numer. Methods Eng.,21, 10. Oct. (1985), 1759–1776.

    Article  MATH  Google Scholar 

  5. Heppler, G.R. and J.S. Hansen,Adv. in Compos. Mater.,1 Aug. (1980), 666–692.

    Google Scholar 

  6. Yeh, J.R. and I.G. Tabjbakhsh,J. Compos. Mater.,20, 4. Jul. (1986), 347–364.

    Google Scholar 

  7. Natarajan, R., S.V. Hoa, and T.S. Sankar,Int. Numer. Methods Eng.,23, 4. Apr. (1986). 623–633.

    Article  MATH  Google Scholar 

  8. Lucking, W.M., S.V. Hoa and T.S. Sankar,J. Compos. Mater.,18, 2. Mar. (1984), 188–198.

    Google Scholar 

  9. Rybicki, E.F.,J. Compos. Mater.,5 (1971), 354–360.

    Google Scholar 

  10. Khalil, S.A., C.T. Sun and W.C. Hwang,Int. J. Fract.,31, 1. May (1986), 37–51.

    Article  Google Scholar 

  11. Moriya, K.,Nippon Kikai Gakkai Ronbunshu a Hen,52, 478, Jun. (1986), 1600–1607.

    Google Scholar 

  12. Spilker, R.L. and D.M. Jakobs,Int. Numer. Methods Eng.,23, 4. Apr. (1986), 555–578.

    Article  MATH  Google Scholar 

  13. Wang, S.S. and F.G. Yuan,J. Appl. Mech.,50 (1983), 835–844.

    Article  MATH  Google Scholar 

  14. Hsu, P.W. and C.T. Herakovich,J. Compos. Mater.,11 (1977), 422–427.

    Google Scholar 

  15. Tang, S.,J. Compos. Mater.,10, 1, Jan. (1976), 69–78.

    Google Scholar 

  16. Bar-Yoseph, P. and T.H.H. Pian,J. Compos. Mater.,15, 3, May (1981), 225–239.

    Google Scholar 

  17. Bar-Yoseph, P. and T.H.H. Pian,Comput. Methods Appl. Mech. Eng.,36, 3, Mar (1983), 309–329.

    Article  MATH  Google Scholar 

  18. Pagano, N.J.,Int. J. Solids Structures,14 (1978), 385–400.

    Article  MATH  Google Scholar 

  19. Wang, J.T.S. and J.N. Dickson,J. Compos. Mater.,12 (1978), 390–401.

    Google Scholar 

  20. Oery, H., H. Reimerdes and S. Dieker,Z. Flugwiss Weltraumforsch,8, 6, Nov.–Dec. (1984), 392–404.

    Google Scholar 

  21. Whitney, J.M. and C.E. Browning,J. Compos. Mater.,6 (1973), 300–303.

    Google Scholar 

  22. Berghaus, D.G. and R.W. Aderholdt,Exp. Mech.,15, 4, Jul. (1975), 173–176.

    Article  Google Scholar 

  23. Spilker, R.L. and S.C. Chou,J. Compos. Mater.,14 (1980), 2–20.

    Google Scholar 

  24. Chien, W.Z.,On the Generalized Variational Principles, Knowledge Press, Shanghai (1985). (in Chinese)

    Google Scholar 

  25. Tsai, S.W. and H.T. Hahn,Introduction to Composite Materials. Technomic Publishing Co. Inc. (1980).

  26. Christensen, R.M.,Mechanics of Composite Materials, John Wiley and Sons Inc. (1979).

  27. Hull, D.,An Introduction to Composite Materials, Cambridge University Press (1981).

Download references

Author information

Authors and Affiliations

  1. Concordia University, Montreal, Canada

    Huang Qian

  2. Shanghai University of Technology, China

    Huang Qian

Authors
  1. Huang Qian
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by Chien, Wei-zang

Rights and permissions

Reprints and permissions

About this article

Cite this article

Qian, H. Variational principle of hybrid energy and the fundamentals of 3-D laminate theory—A new approach for the analysis of interlaminar stresses in composite laminates. Appl Math Mech 9, 649–657 (1988). https://doi.org/10.1007/BF02465694

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02465694

Keywords

Search

Navigation