Abstract
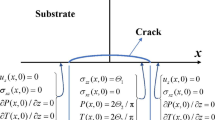
Field equations of the non-local elasticity are solved to determine the state of stress in a plate with a Griffith crack subject to uniform tension. Then a set of dual-integral equations is solved using a new method, namely Schmidt's method. This method is more exact and more reasonable than Eringen's one for solving this kind of problem. Contrary to the solution of classical elasticity, it is found that no stress singularity is present at the crack tip. The significance of this results is that the fracture criteria are unified at both the macroscopic and the microscopic scales. The finite hoop stress at the crack tip depends on the crack length.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Eringen A C, Speziale C G, Kim B S. Crack tip problem in non-local elasticity[J].Journal of Mechanics and Physics of Solids, 1977,25(5):339.
Eringen A C. Linear crack subject to shear[J].International Journal of Fracture, 1978,14(4):367–379.
Eringen A C, Linear crack subjects to antiplane shear[J].Engineering Fracture Mechanics, 1979,12(2):211–219.
Zhou Zhengong, Han Jiecai, Du Shangyi. Investigation of the scattering of harmonic elastic waves by a finite crack using the non-local theory[J].Mechanics Research Communications, 1998,25(5):519–528.
Zhou Zhengong, Wang Biao, Du Shangyi. Scattering of the anti-plane shear waves by a finite crack by using the non-local theory[J].International Journal of Fracture, 1998,91(4):13–22.
Nowinski J L. On non-local aspects of the propagation of Love waves[J].International Journal of Engineering Science, 1984,22(4):383–392.
Nowinski J L. On non-local theory of wave propagation in elastic plates[J].ASME Journal Applied Mechanics, 1984,51(3):608–613.
Eringen A C. Continuum mechanics at the atomic scale[J].Crystal Lattice Defects, 1977,7(2):109–130.
Eringen A C. Non-local elasticity and waves[A]. In: P Thoft-Christensen Ed.Continuum Mechanics Aspects of Geodynamics and Rock Fracture Mechanics[C]. Holland: Dordrecht, 1974,81–105.
Morse P M, Feshbach H.Methods of Theoretical Physics[M]. Vol. 1 New York: McGraw-Hill, 1958.
Gradshteyn I S, Ryzhik I M.Table of Integral, Series and Products[M] New York: Academic Press, 1980.
Erdelyi A.Tables of Integral Transforms[M]. Vol.1, New York: McGraw-Hill, 1954.
Amemiya A, Taguchi TNumerical Analysis and Fortran[M]. Tokyo: Maruzen, 1969.
Itou S. Three dimensional waves propagation in a cracked elastic solid[J].ASME Journal of Applied Mechanics, 1978,45(3):808–811.
Itou S. Three dimensional problem of a running crack[J].International Journal of Engineering Science, 1979,17(4):59–71.
Eringen A C. Interaction of a dislocation with a crack[J].Journal of Applied Physics, 1983,54(3):6811–6818.
Author information
Authors and Affiliations
Additional information
Foundation item: the National Foundation for Exellent Young Investigators (19725209)
Rights and permissions
About this article
Cite this article
Zhengong, Z., Biao, W. Investigation of a griffith crack subject to uniform tension using the non-local theory by a new method. Appl Math Mech 20, 1099–1107 (1999). https://doi.org/10.1007/BF02460326
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02460326