Abstract
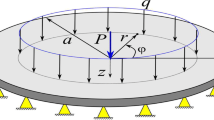
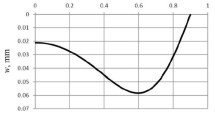
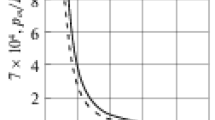
In this paper, a new method, the exact analytic method, is presented on the basis of step reduction method. By this method, the general solution for the bending of nonhomogenous circular plates and circular plates with a circular hole at the center resting on an elastic foundation is obtained under arbitrary axial symmetrical loads and boundary conditions. The uniform convergence of the solution is proved. This general solution can also be applied directly to the bending of circular plates without elastic foundation. Finally, it is only necessary to solve a set of binary linear algebraic equation. Numerical examples are given at the end of this paper which indicate satisfactory results of stress resultants and displacements can be obtained by the present method.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Timoshenko, S. and S. Woinowsky-krieger,Theory of plates and shells, McGraw-Hill book company (1959), Second Edition.
Shen Xi-ying and Zheng Da-tong, Deflections of a circular plate resting on Winkler subgrade solved by the boundary element,Engineering Mechancis,2, 2 (1985), 10–20. (in Chinese)
Wen Pi-hua, Point intensity method of solving circular plate resting on elastical subgrade,Engineering Mechanics,4, 2 (1987), 18–26. (in Chinese)
Yeh Kai-yuan, General solutions on certain problems of elasticity with non-homogeneity and variable thickness, IV. Bending, buckling and free vibration of non-homogeneous variable thickness beams,Journal of Lanzhou University, Special Number of Mechanics, 1 (1979), 133–157. (in Chinese)
Ji Zhen-yi, The convergent condition and united formula of step reduction method,Applied Mathematics and Mechanics,9, 12 (1988), 1183–1193.
Author information
Authors and Affiliations
Additional information
Communicated by Yeh Kai-yuan
Rights and permissions
About this article
Cite this article
Zhen-yi, J. The general solution for axial symmetrical bending of nonhomogeneous circular plates resting on an elastic foundation. Appl Math Mech 12, 871–879 (1991). https://doi.org/10.1007/BF02458252
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02458252