Abstract
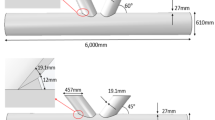
In this paper fatigue strength of T-type tubular joints subjected to in-plane bending or out-of-plane bending load is investigated. By considering material constants and initial crack sizes as random variables and applying Monte Carlo simulation method, we have given a statistical analysis on fatigue life. Simultaneosly, linear regression analyses of computed results are performed and compared with that of the known experimental data.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Newman, J. C. and I. S. Raju, An empirical stress-intensity factor equation for the surface crack,Engineering Fracture Mechanics,15, 1–2 (1981), 185-192.
Lawrence, F. V., N. J. Ho, and P. K. Mazumdar. Predicting the fatigue resistance of welds,Ann. Rev. Mater. Sci.,11 (1981), 401–425.
Peterson, R. E., Notch-SensitivityMetal Fatigue edited by G. Sines, and J. L. Waisman, McGraw-Hill, NY, (1959).
Research Group on Probalility and Statistics, Computer Center of Academy of Science of China,Probabilistic and Statistical Computation, Science Press, Beijing, (1979). (in Chinese)
Sang, G. G. and Zhang, S. K.,Structural Reliability Principle and Its Application. Shanghai Jiaotong University Press (1986). (in Chinese)
McDonald, A. and J. G. Wylde, Experimental results of fatigue tests on tubular welded joints,Fatigue Offshore Structural Steels. Thomas Telford Ltd., London, (1981).
Van Delft D. R. V. et al., The Calculation of Fatigue Crack Growth in Welded Tubular Joints Using Fracture Mechanics. OTC. (1986), 573–582.
Engesvik, K. M. and T. Moan, Probabilistic analysis of the uncertainty in the fatigue capacity of welded joints,Engineering Fracture Mechanics,18, 4 (1983), 743–762.
Kirkemo, F., Applications of probabilistic fracture mechanics to offshore structures,Appl. Mech. Rev. 41 2 (1988), 61–84.
DnV (1984).
Connolly, M. P. and W. D. Dover, On the fatigue fracture mechanics analysis of tubular joints,Proc. OMAE, Huston 7–8 April (1987), 287–293.
Zhang Y. H. et al., The fatigue life prodiction of welded joints by using statistical analysis method.Ocean Engineering,8, 4 (1990), 15–23. (in Chinese)
Zheng X. X. et al.Fracture and Fatigue Analysis on Structures in Naval Architecture and Ocean Engineering. Ocean Press, Beijing, (1988). (in Chinese)
Fang Z. G.,Computer Simulation and MC Method, Beijing Institute of Technology Press, Beijing, (1988), (in Chinese)
Hudak Jr. S. J. et al.,Analysis of Corrosion Fatigue Crack Growth in Welded Tubular Joints, OTC, (1984), 495–507.
Wu, S. X. Shape change of surface crack during fatigue growth.Engineering Fracture Mechanics.22, 5 (1985), 897–913.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Guo-hua, N., Zhi-yuan, W. & Ren-huai, L. Application of the probabilistic fracture mechanics method of predicting the fatigue life of tubular joints. Appl Math Mech 15, 1017–1023 (1994). https://doi.org/10.1007/BF02455393
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02455393