Skip to main content
SpringerLink
Log in

Bifurcation analysis of a mitotic model of frog eggs

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

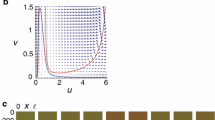
The mitotic model of frog eggs established by Borisuk and Tyson is qualitatively analyzed. The existence and stability of its steady states are further discussed. Furthermore, the bifurcation of above model is further investigated by using theoretical analysis and numerical simulations. At the same time, the numerical results of Tyson are verified by theoretical analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Borisuk M T, Tyson J J. Bifurcation analysis of a model of mitotic control in frog eggs [J].Journal of Theoretical Biology, 1998,195(1):69–85.

    Article  Google Scholar 

  2. Novak B, Tyson J J. Numerical analysis of a comprehensive model of M-phase control in Xenopus oocyte extracts and intact embryos[J].Journal of Cell Science, 1993,106(4):1153–1168.

    Google Scholar 

  3. Novak B, Tyson JJ. Modeling the cell division cycle: M-phase trigger, oscillations, and size control [J].Journal of Theoretical Biology, 1993,165(1): 101–134.

    Article  Google Scholar 

  4. ZHENG Zuo-huan, ZHOU Tian-shou, ZHANG Suo-chun. Dynamical behavior in the modeling of cell division cycle [J].Chaos, Solitons & Fractals, 2000,11(4):2371–2378.

    Article  MathSciNet  Google Scholar 

  5. FENG Bei-ye, ZENG Xuan-wu. Qualitative analysis of a mitotic model of frog eggs [J].Acta Mathematicae Applicatae Sinica, 2002,25(3):460–468. (in Chinese)

    MathSciNet  Google Scholar 

  6. ZHANG Suo-chun. Oregonator: General results of positive steady state and its stability [J].Chinese Science Bulletin, 1996,41(10):798–804.

    MathSciNet  Google Scholar 

  7. ZHANG, Suo-chun.Mathematical Theory and Numerical Method of Modern Oscillatory Reaction [M]. Zhengzhou: Henan Scientific and Technic Press, 1991. (in Chinese)

    Google Scholar 

  8. ZHANG Jin-yuan, FENG Bei-ye.Geometric Theory and Bifurcation Problem of Ordinary Differential Equation [M]. Beijing: Peking University Press, 2000. (in Chinese)

    Google Scholar 

  9. Hassard B D, Kazarinoff N D, Wan Y H.Theory and Application of Hopf Bifurcation [M]. England: Cambridge University Press, 1981.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Systems Science, Academy of Mathematics and System Sciences, Chinese Academy of Sciences, 100080, Beijing, PR China

    Lü Jin-hu Doctor

  2. Institute of Applied Mathematics, Academy of Mathematics and System Sciences, Chinese Academy of Sciences, 100080, Beijing, P.R. China

    Zhang Zi-fan & Zhang Suo-chun

Authors
  1. Lü Jin-hu Doctor
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhang Zi-fan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhang Suo-chun
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by LI Jia-chun

Foundation items: the National Natural Science Foundation of China (10171099); K. C. Wong Education Foundation, Hong Kong

Biography: Lü Jin-hu(1974-)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jin-hu, L., Zi-fan, Z. & Suo-chun, Z. Bifurcation analysis of a mitotic model of frog eggs. Appl Math Mech 24, 284–297 (2003). https://doi.org/10.1007/BF02438266

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02438266

Key words

Chinese Library Classification

2000 MR Subject Classification

Search

Navigation