Abstract
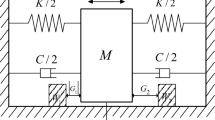
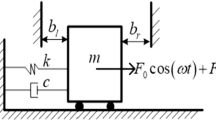
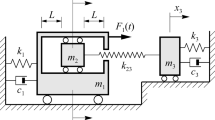
A method is presented to seek for coexisting periodic orbits which may be stable or unstable in piecewise-linear vibro-impacting systems. The conditions for coexistence of single impact periodic orbits are derived, and in particular, it is investigated in details how to assure that no other impacts will happen in an evolution period of a single impact periodic motion. Furthermore, some criteria for nonexistence of single impact periodic orbits with specific periods are also established. Finally, the stability of coexisting periodic orbits is discussed, and the corresponding computation formula is given. Examples of numerical simulation are in good agreement with the theoretic analysis.
Similar content being viewed by others
References
Guckenheimer J, Holmes P.Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields[M]. New York: Springer-Verlag, 1986.
Wigins S.Introduction to Applied Nonlinear Dynamical Systems and Chaos[M]. (Reprinted) New York: Springer-Verlag, 1991.
Wiggins S.Global Bifurcations and Chaos, Analytical Methods[M]. New York: Springer-Verlag, 1988.
Bazejczyk-Okolewska B, Kapitaniak T. Co-existing attractors of impact oscillator[J].Chaos, Solitons & Fractals, 1998,9(8):1439–1443.
Feudel U, Grebogi C, Poon L, Yorke J A. Dynamical properties of a simple mechanical system with a large number of coexisting periodic attractors[J].Chaos, Solitons & Fractals, 1998,9(1/2):171–180.
Whiston G S. Global dynamics of a vibro-impacting linear oscillator[J].J Sound Vib, 1987,118 (3):395–424.
Shaw S W, Holmes P J. A periodically forced piecewise linear oscillator[J].J Sound Vib, 1983,90 (1):129–155.
Ivanov A P. Stabilization of an impact oscillator near grazing incidence owing to resonance[J].J Sound Vib, 1993,162(3):562–565.
Whiston G S. Impacting under harmonic excitation[J].J Sound Vib, 1979,67(2):179–186.
Whiston G S. The vibro-impact response of a harmonically excited and preloaded one-dimensional linear oscillator[J].J Sound Vib, 1987,115(2):303–319.
Nordmark A B. Non-periodic motion caused by grazing incidence in an impact oscillator[J].J Sound Vib, 1991,145(2):279–297.
Foale S, Bishop S R. Dynamical complexities of forced impacting systems[J].Phil Trans Royal Soc London A, 1992,338(4):547–556.
Nordmark A B. Effects due to low velocity in mechanical oscillators[J].Int J Bifurcation and Chaos, 1992,2(3):597–605.
Shaw S W, Rand R H. The transition to chaos in a simple mechanical system[J].Int J Nonlinear Mech, 1989,24(1):41–56.
Author information
Authors and Affiliations
Additional information
Communicated by Chen Yu-shu
Foundation items: the National Natural Science Foundation of China (19990510, 19872010); the Doctoral Foundation of National Educational Ministry of China (98000619)
Biographies: Li Qun-hong (1964-) Lu Qi-shao (1940-)
Rights and permissions
About this article
Cite this article
Qun-hong, L., Qi-shao, L. Coexisting periodic orbits in vibro-impacting dynamical systems. Appl Math Mech 24, 261–273 (2003). https://doi.org/10.1007/BF02438264
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02438264