Abstract
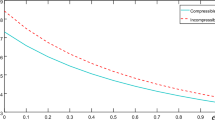
An investigation is made of the magnetic Rayleigh problem where a semi-infinite plate is given an impulsive motion and thereafter moves with constant velocity in a non-Newtonian power law fluid of infinite extent. The solution of this highly non-linear problem is obtained by means of the transformation group theoretic approach. The one-parameter group transformation reduces the number of independent variables by one and the governing partial differential equation with the boundary conditions reduce to an ordinary differential equation with the appropriate boundary conditions. Effect of the some parameters on the velocity u (y, t) has been studied and the results are plotted.
Similar content being viewed by others
References
Gerhart P M.Fundamentals of Fluid Mechanics [M]. Wesly Publishing Comp Inc. 1993, 11–20.
Vujanovic B, Stauss A M, Djukic Dj, A variational solution of the Rayleigh problem for a power law non-Newtonian conducting fluid [J].Ingenieur-Archiv, 1972,41:381–386.
Sapunkov Ya G. Rayleigh problem of non-Newtonian electroconductive fluids [J].J Appl Math Tech Physics 1970,2:50–55.
Vujanovic B. An approach to linear and nonlinear heat transfer problem using a Lagrangian [J].J AIAA, 1971,9:327–330.
Birkhoff G. Mathematics for engineers [J].Elect Eng, 1948,67:1185–1192.
Morgan A J A. The reduction by one of the number of independent variables in some systems of nonlinear partial differential equations [J].Quart J Math Oxford, 1952,3(2):250–259.
Abd-el-Malek M B, Badran N A. Group method analysis of unsteady free-convective laminar boundary-layer flow on a nonisothermal vertical circular cylinder [J].Acta Mechanica, 1990,85: 193–206.
Abd-el-Malek M B, Boutros YZ, Badran N A. Group method analysis of unsteady free-convective boundary-layer flow on a nonisothermal vertical flat plate [J].J Engineering Mathematics, 1990,24:343–368.
Boutros Y Z, Abd-el-Malek M B, El-Awadi A, et al. Group method for temperature analysis of thermal stagnant lakes [J].Acta Mechanica, 1999,114:131–144
Fayez H M, Abd-el-Malek M B. Symmetry reduction to higher order nonlinear diffusion equation [J].Int J Appl Math, 1999,1:537–548.
Ames W F. Similarity for the nonlinear diffusion equation [J].J & EC Fundamentals, 1965,4: 72–76.
Moran M J, Gaggioli RA. Reduction of the number of variables in partial differential equations with auxiliary conditions [J].SIAM J Applied Mathematics, 1968,16:202–215.
Burden R, Faires D.Numerical Analysis [M] Prindle: Weberand Scmidt, 1985.
Author information
Authors and Affiliations
Additional information
Communicated by WU Cheng-ping
Biographies: M. B. Abd-el-Malek
Rights and permissions
About this article
Cite this article
Abd-el-Malek, M.B., Badran, N.A. & Hassan, H.S. Solution of the Rayleigh problem for a powerlaw non-Newtonian conducting fluid via group method. Appl Math Mech 23, 639–646 (2002). https://doi.org/10.1007/BF02437647
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02437647