Skip to main content
SpringerLink
Log in

Singularly perturbed boundary value problems for semi-linear retarded differential equations with nonlinear boundary conditions

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

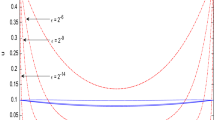
A boundary value problems for functional differenatial equations, with nonlinear boundary condition, is studied by the theorem of differential inequality. Using new method to construct the upper solution and lower solution, sufficient conditions for the existence of the problems' solution are established. A uniformly valid asymptotic expansions of the solution is also given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Lange C G, Miura R M, Singular perturbation analysis of boundary value problem for differential difference equations[J].SIAM J Appl Math, 1982,42(3): 502–503.

    Article  MATH  MathSciNet  Google Scholar 

  2. MIAO Shu-mei, ZHOU Qin-de. The asymptotic expansions of singularly perturbed boundary value problems for semi-linear differential difference equations[J].Northeastern Math J, 1989,5(3): 283–293.

    Google Scholar 

  3. ZHOU Qin-de, MIAO Shu-mei. The boundary value problem for differential difference equations [J].Acta Math Sinica, 1989,32(1): 55–70. (in Chinese)

    MathSciNet  Google Scholar 

  4. LU Shi-ping. A kind of singularly perturbed boundary value problems for nonlinear Volterra functional differential equations[J].Ann Differential Equations, 1998,14(2): 247–253.

    MathSciNet  Google Scholar 

  5. LU Shi-ping. A kind of singularly perturbed boundary value problems for nonlinear Volterra functional differential equations[J].Appl Math Chinese Univ, Ser B, 2000,15(2): 137–142.

    Google Scholar 

  6. Klasen G A. Differential inequalities and existence theorems for second order boundary value problems[J].Differential Equations, 1971,10(4): 529–531.

    MathSciNet  Google Scholar 

  7. Hale J.Theory of Functional Differential Equations[M]. New York: Springer-Verlag, 1977.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Beijing Institute of Technology, 100081, Beijing, P. R. China

    Ren Jing-li (Lecturer, Doctor Candidate) & Ge Wei-gao

  2. Department of Mathematics, Zhengzhou University, 450052, Zhengzhou, P. R. China

    Ren Jing-li (Lecturer, Doctor Candidate)

Authors
  1. Ren Jing-li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ge Wei-gao
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Communicated by Lin Zong-chi, Original Member of Editorial Committee, AMM

Foundation item: the National Natural Science Foundation of China (19871005)

Biography: Ren Jing-li (1973≈)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jing-li, R., Wei-gao, G. Singularly perturbed boundary value problems for semi-linear retarded differential equations with nonlinear boundary conditions. Appl Math Mech 24, 1450–1455 (2003). https://doi.org/10.1007/BF02435586

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02435586

Key words

Chinese Library Classification number

2000 Mathematics Subject Classification

Search

Navigation