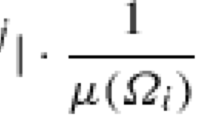Abstract
We consider the integrated density of statesN(λ) of the difference Laplacian −Δ on the modified Koch graph. We show thatN(λ) increases only with jumps and a set of jump points ofN(λ) is the set of eigenvalues of −Δ with the infinite multiplicity. We establish also that
whered s =2log5/log(40/3) is the spectral dimension of MKG.
Similar content being viewed by others
References
[B] Brolin, H.: Invariant sets under iteration of rational functions. Arkiv for Matematik6, 103–144 (1965)
[F] Fukushima, M.: Dirichlet forms, diffusion processes and spectral dimension for nested fractals. Ideas and Meth. in Math. Anal. Stoch. Appl.1. Cambridge: Cambridge University Press (to appear)
[FS] Fukushima, M., Shima, T.: On a spectral analysis for the Sierpinski gasket. Preprint (1989)
[H] Hutchinson, J.E.: Fractals and self-similarity. Indiana Univ. Math. J.30, 713–747 (1981)
[K] Kuczma, M.: Functional equations in a single variable. Warszawa: Polish Scientific Publishers 1968
[M] Malozemov, L.A.: Difference Laplacian Δ on the modified Koch curve. Russ. J. Math. Phys.3, 1 (1992)
[R] Rammal, R.: Spectrum of harmonic excitations on fractals. J. Phys.45, 191–206 (1984)
Author information
Authors and Affiliations
Additional information
Communicated by B. Simon
Rights and permissions
About this article
Cite this article
Malozemov, L. The integrated density of states for the difference Laplacian on the modified Koch graph. Commun.Math. Phys. 156, 387–397 (1993). https://doi.org/10.1007/BF02098488
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02098488