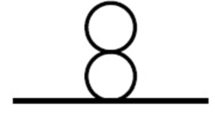Abstract
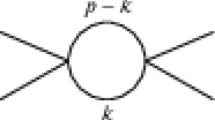
As an application of the theory of solutions of the classical, Euclidean field equation, we prove the existence of solutions to the renormalized functional field equation, for the λΦ4 interaction in four Euclidean space dimensions, with non-negative λ and nonzero mass, through orderℏc. That is, we prove that the functional derivative of the connected generating functional is in the Schwartz space Reℒ(R 4), when evaluated at external sources in Reℒ, through orderℏc. We also prove the existence of all functional derivatives of the connected generating functional through the same order. All quantities of interest are analytic in the coupling constant at 0≦λ<∞, and continuous in the external source.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Jackiw, R.: Functional evaluation of the effective potential. Phys. Rev. D9, 1686–1701 (1974)
Reed, M., Simon, B.: Methods of modern mathematical physics, Vol. II. New York: Academic Press 1975
Reed, M.: Abstract nonlinear wave equations. Berlin-Heidelberg-New York: Springer 1976
Osterwalder, K., Schrader, R.: Axioms for Euclidean Green's functions. Commun. Math. Phys.31, 83–112 (1973)
Nelson, E.: Construction of quantum fields from Markoff fields. J. Funct. Anal.12, 97–112 (1973)
Hepp, K.: Renormalization theory. In: Statistical mechanics and quantum field theory. Université de Grenoble—Summer School of Theoretical Physics, Les Houches 1970 (eds. C. DeWitt, R. Stora), pp. 429–500. New York: Gordon and Breach 1971
Epstein, H., Glaser, V.: Le rôle de la localité dans la rénormalisation perturbative en théorie quantique des champs. In: Statistical mechanics and quantum field theory. Université de Grenoble—Summer School of Theoretical Physics, Les Houches 1970 (eds. C. DeWitt, R. Stora), pp. 501–545. New York: Gordon and Breach 1971
Goldstone, J., Jackiw, R.: Quantization of nonlinear waves. Phys. Rev. D11, 1486–1498 (1975)
Rauch, J., Williams, D. N.: Euclidean classical field equations forn ≦ 4 dimensions (unpublished)
Boulware, D., Brown, L.: Tree graphs and classical fields. Phys. Rev.172, 1628–1631 (1968)
Jost, R., Hepp, K.: Über die Matrixelemente des Translations Operators. Helv. Phys. Acta35, 34–46 (1962)
Author information
Authors and Affiliations
Additional information
Communicated by J. Glimm
Rights and permissions
About this article
Cite this article
Williams, D.N. The Euclidean loop expansion for massive λΦ 44 : Through one loop. Commun.Math. Phys. 54, 193–218 (1977). https://doi.org/10.1007/BF01614084
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01614084