An upper bound on the free energy for classical systems with Coulomb interactions in a varying external field

Abstract

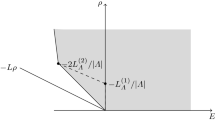
The thermodynamic limit is taken using a sequence of regions all the same shape as a given region ω of volume |ω|, with a specified distribution of normal field component on ∂ω. We show that with magnetostatic interactions the limiting free energy density is bounded above by jhen where$\bar f$(ϱ,B) is the free energy density for a system of density ϱ in a uniform external fieldB and the “inf” is taken over all divergence-free fieldsB with given normal component on ∂ω and all densities ϱ(x) compatible with particle number constraints of the form$\int\limits_{\Gamma _i } {\varrho (x)d^3 x = \left| {\Gamma _i } \right|\varrho _i }$ where Γ_i is a sub-region of ω. A physical argument suggests that this upper bound is the true thermodynamic limit, and that it takes account demagnetization effects. Electrostatic interactions can be treated similarly.