Skip to main content
SpringerLink
Log in

Existence and approximation theorems on a weakly 1-complete analytic space

  • Published:
manuscripta mathematica Aims and scope Submit manuscript

Abstract

Let (X,XΘ) be a weakly 1-complete analytic space with an exhausting plurisubharmonic function

, B a positive line bundle over X and

a coherent analytic sheaf on X. Then, for any c, d ∈ ℝ(c<d), there exists a positive integer p0 such that the restriction mapping

has a dense image for P≧P0, where

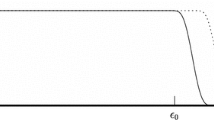
for all a ∈ ℝ. An existence theorem for sections of sheaf

is also given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. FJIKI, A.: On the blowing down of analytic spaces. Publ. R. I. M. S. Kyoto Univ.10, 473–507 (1975)

    Google Scholar 

  2. GRAUERT, H.: Bemerkenswerte pseudokonvexe Mannigfaltigkeiten. Math. Z.81, 377–391 (1963)

    Google Scholar 

  3. GRAUERT, H., REMMERT, R.: Bilder und Urbilder analytischer Garben. Math. Ann.68, 393–443 (1958)

    Google Scholar 

  4. GUNNING, R. C., ROSSI, H.: Analytic functions of several complex variables. Prentice-Hall, Englewood Cliffs, N. J. 1965

    Google Scholar 

  5. KAZAMA, H.: On pseudoconvexity of complex abelian Lie groups. J. Math. Soc. Japan25, 329–333 (1973)

    Google Scholar 

  6. KAZAMA, H.: Approximation theorem and application to Nakano's vanishing theorem for weakly 1-complete manifolds. M. F. S. Kyushu Univ.27, 221–240 (1973)

    Google Scholar 

  7. MORIMOTO, A.: Non-compact complex Lie groups without non-constant holomorphic functions. P. C. on Complex Analysis at Univ. of Minneapolis, 256–272 (1965)

  8. — On the classification of non-compact complex abelian Lie groups. Trans. Amer. Math. Soc.123, 200–228 (1966)

    Google Scholar 

  9. NAKANO, S.: On complex analytic vector bundle. J. Math. Soc. Japan7, 1–12 (1955)

    Google Scholar 

  10. — On the inverse of monoidal transformation. Publ. R. I. M. S. Kyoto Univ.6, 483–502 (1970/71)

    Google Scholar 

  11. —: Vanishing theorem for weakly 1-complete manifolds. Alg. Geom. and Comm. Alg., Kinokuniya, Tokyo, 169–179 (1973)

    Google Scholar 

  12. ROSSI, H.: Picard variety of an isolated singular point. Rice Univ. Studies54, 63–73 (1968)

    Google Scholar 

  13. Seminaire Henri Cartan. E. N. S. 1950/51

  14. TAKEUCHI, S.: On completeness of holomorphic principal bundles. Nagoya Math. J.57, 121–138 (1974)

    Google Scholar 

Download references

Author information

Author notes

  1. Hideaki Kazama

    Present address: Mathematisches Seminar der Universität Hamburg, D-2000, Hamburg 13, Bundesstr. 55

Authors and Affiliations

  1. Department of Mathematics College of General Education, Kyushu University, Ropponmatsu, 810, Fukuoka, Japan

    Hideaki Kazama

Authors
  1. Hideaki Kazama
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This work was supported by a grant from the Alexander von Humboldt Foundation.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kazama, H. Existence and approximation theorems on a weakly 1-complete analytic space. Manuscripta Math 19, 57–74 (1976). https://doi.org/10.1007/BF01172338

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01172338

Keywords

Search

Navigation