Abstract
Purpose of Review
This paper reviews the recent literature on numerical modelling of the dynamics of the Greenland ice sheet with the goal of providing an overview of advancements and to highlight important directions of future research. In particular, the review is focused on large-scale modelling of the ice sheet, including future projections, model parameterisations, paleo applications and coupling with models of other components of the Earth system.
Recent Findings
Data assimilation techniques have been used to improve the reliability of model simulations of the Greenland ice sheet dynamics, including more accurate initial states, more comprehensive use of remote sensing as well as paleo observations and inclusion of additional physical processes.
Summary
Modellers now leverage the increasing number of high-resolution satellite and air-borne data products to initialise ice sheet models for centennial time-scale simulations, needed for policy relevant sea-level projections. Modelling long-term past and future ice sheet evolution, which requires simplified but adequate representations of the interactions with the other components of the Earth system, has seen a steady improvement. Important developments are underway to include ice sheets in climate models that may lead to routine simulation of the fully coupled Greenland ice sheet–climate system in the coming years.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The Greenland ice sheet (GrIS) is the second largest ice body on Earth and is expected to be a major contributor to future sea-level rise [1]. Potential threshold behaviour in response to a warming Arctic may cause a long-term and irreversible retreat of the ice sheet for warming levels that could be realised within this century [2,3,4]. Understanding its past, present and future behaviour is therefore of both great scientific interest and societal concern.
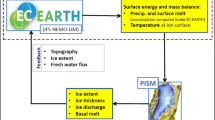
Projecting future changes and studying the past behaviour of the GrIS and its interactions with other components of the Earth system requires numerical ice sheet models built around a physical description of ice sheet flow (Fig. 1). In its present state, the GrIS gains mass by snow accumulation at higher elevations and flows by deformation under its own weight and by sliding over a bed of rock and/or sedimentary material. At its margins, the ice sheet loses mass mainly by surface meltwater runoff, ocean-driven melting and iceberg calving from a large number of marine-terminating outlet glaciers. Its total mass change is determined by the sum of the surface mass balance (SMB), basal mass balance (melting or freezing under the ice sheet) and mass exchange of the marine-terminating outlet glaciers with the ocean, today predominantly occurring in the form of calving of icebergs that eventually melt in ocean waters [5].
Elements of a typical Greenland ice sheet model (blue) and possible interactions with the other components of the Earth system (orange). Mass exchange processes are shown in green. Changes in ice sheet size, mass and local ice thickness affect the properties of atmosphere, ocean and solid Earth and vice versa. Key processes for the ice sheet model itself are the ice temperature evolution and the flow of the ice caused by deformation and sliding, depending primarily on ice thickness, surface slope and ice temperature
The rate of ice deformation is strongly dependent on ice thickness, surface slope and rheological properties of the ice and the underlying substrate, which change considerably with changing temperature, impurity concentration and water content of the ice. Thermodynamic coupling is needed to model the long-term (millennial to multi-millennial) evolution as the ice sheet responds to climate changes and might only be neglected for short-term (decadal to centennial time scale) simulations. Another long-term interaction mechanism of the ice sheet concerns isostatic bedrock adjustment under the varying load of the ice. The millennial to multi-millennial response time scales associated with bedrock changes and thermodynamics have led to the use of spin-up techniques that consist of running ice sheet models with boundary conditions of simulated or reconstructed past climate changes to capture the long-term memory of these processes [4, 6].
However, the present-day configuration of the ice sheet simulated with such long-term reconstructions shows a rather large discrepancy when compared with available satellite and airborne observations [7, 8]. Studies focusing on current mechanisms affecting ice sheet dynamics and short-term evolution of ice sheets also need an accurate representation of the present-day ice sheet configuration and may therefore rely on observations to initialise models: they infer poorly known englacial or subglacial parameters and boundary conditions using data assimilation techniques of observed surface conditions [9, 10].
GrIS numerical models vary largely in terms of the processes they include, the spatial resolution of their underlying grids and the forcings they apply [11] depending on the time periods of interest and the scientific questions they address. This is similar for the level of detail contained in simulated interactions with the other components of the Earth system. Climatic boundary conditions may, e.g., be prescribed, estimated from simple parameterisations or calculated with full complexity climate models, with either one-directional or two-way coupling between ice sheet and climate models.
Acknowledging considerable overlap between them, we discuss three different approaches to GrIS modelling in this paper: (1) The long-term modelling approach with thermodynamic coupling and isostatic bedrock adjustment, requiring spin-up techniques, (2) data assimilation techniques, typically applied to model initialisation for centennial time-scale projections, making extensive use of high-resolution observations of the present-day ice sheet with inversion techniques, (3) fully coupled ice sheet–climate modelling of different levels of complexity to physically represent feedbacks between the ice sheet, atmosphere and ocean. All three modelling approaches, for example, are represented in the GrIS model initialisation experiments (initMIP-Greenland) [12] performed within the context of the Ice Sheet Model Intercomparison Project for CMIP6 (ISMIP6) [13]. It should be noted that many of the issues discussed here could be equally applied to other ice sheet domains, like Antarctica [14].
Distinguishing between the different approaches is somewhat arbitrary but, in many cases, derives from the specific goals of individual research groups. In fact, closer collaboration across these boundaries could further advance the ice sheet modelling community and should be encouraged. None of the modelling approaches can be completely separated from the others. Aside from appreciating the strengths and limitations of the different approaches for specific model applications, the aim of this review paper is therefore also to stimulate possible directions of future research and cross-fertilisation between different groups. It is in this spirit that we have decided to discuss the different research priorities in one review paper.
Ingredients of Numerical Models for the Greenland Ice Sheet
In this section, we review recent developments concerning specific aspects of large-scale GrIS modelling.
Discretisation and Grid Representation
Domain discretisation is central to any numerical problem. Models used for long-term simulations nowadays typically apply regular equidistant grids at a horizontal resolution of 5–20 km [15,16,17], but very high resolutions have been achieved with massively parallel computational efforts [8]. Finite element grids of variable spatial resolution, with the smallest elements sometimes below kilometre-scale resolution, are also applied, mainly for short-term simulation and data assimilation problems [18,19,20,21]. In order to capture critical areas while keeping computational resources manageable, some models have integrated a relatively new approach for large-scale ice sheet simulations by including an adaptive mesh that is updated during runtime, following grounding line or ice front migration [22]. This technique has been applied to capture details of outlet glacier behaviour with a local resolution of 500 m, while a base grid of 8 km is used for most of the ice sheet [23].
Approximations to the Stress Balance Equation
As ice is a viscous incompressible fluid, it is best modelled using full-Stokes equations. Due to the intensive computational resources needed to solve these equations and the thin aspect ratio of ice sheets, several approximations based on asymptotic developments of these equations have been derived [24]. These can be used to reduce computation time substantially, allowing large-scale simulations to be run with limited resources [9, 25]. Interior regions dominated by vertical shearing are captured well with these simple approximations, while fast-flowing outlet glaciers at the ice sheet margins are best calculated using the full-Stokes solution [26, 27]. Several techniques have been used to combine different approximations [28,29,30].
While a Stokes model without any approximation remains the best description of ice sheet flow and has been successfully applied for the GrIS on a century time scale [31, 32], it is by now appreciated that certain approximations and combinations thereof represent feasible alternatives to describe full ice sheet–shelf systems on large scale [33]. This is, in particular, the case in the light of other large uncertainties introduced, e.g. by the SMB forcing and other boundary conditions that have a larger impact on ice sheet evolution than choices made concerning the stress balance approximations [31]. Recent attempts have been made to simulate the ice sheet by relying on the shallow shelf approximation in combination with extensive data assimilation techniques [20, 34, 35]. However, the potential consequences of using these approximations to simulate ice dynamics for past and future ice sheet evolution are not well known.
Thermodynamics and Ice Rheology
Ice sheet thermodynamics are an important element of long-term ice sheet modelling, since ice deformation is non-linearly dependent on ice temperature. In addition, large parts of the GrIS are at the pressure melting point, implying an active role for basal sliding as well. In order to compute both cold and temperate ice properties with a single energy-conserving framework, many models now included an enthalpy framework [36] and a rheology that accounts for water fraction in temperate ice [37]. Enthalpy models compute significantly larger basal melt rates and thinner temperate ice thickness than cold ice models [36].
To aid understanding the evolution of the ice sheet interior, thermodynamic modelling has been used to explain the reconstructed temperature recovered from a Greenland deep ice core [38]. The results indicate that the model can only be reconciled with reconstructions when a combination of different processes, including strain heating and cryo-hydrologic warming in deep crevasses, induced by water infiltration and latent heat exchange [39], is invoked.
Anisotropy is another potential source of discrepancies between observed and modelled ice properties, as rheological laws used in most ice sheet models rely on the isotropic Glen’s flow law [40]. Deep ice cores and radar observations suggest more complex ice rheologies [41, 42] that might explain observed large-scale ice folding [43].
An evaluation of the impact of observationally constrained thermal boundary conditions on the modelled thermomechanical state in western Greenland has shown that there is a strong influence of the surface thermal boundary [44].
A study of the geothermal heat flux distribution beneath the GrIS [45] concludes that present-day basal melt rates and their expression at the surface, like the North East Greenland Ice Stream (NEGIS), may be related to anomalies arising from plate tectonic movements dating back tens of millions of years. Finally, the long-term future evolution of the ice sheet thermal state has been schematically simulated with a thermodynamic model [46] to study the possibility of a thermal-viscous collapse, which implies that the ice sheet disintegration is accelerated by warming of the ice. Results indicate that the lower part of the ice column where most of the deformation occurs could be warmed to the pressure-melting point within a few centuries [46].
Ice Sheet Basal Conditions
The thermal condition at the base of the ice sheet is known to have important consequences for basal meltwater production and hence for the basal friction and sliding velocity [47]. This view is extended with a study on the sliding of temperate basal ice that may contribute significantly to ice flow in some regions [48]. However, even the basal thermal state (whether ice is frozen or thawed) of the GrIS is poorly known, with at least one third of its area being highly uncertain [49]. Aside from thermal conditions, the basal topography exerts an important control on the flow speed of Greenland outlet glaciers, as shown for Humboldt glacier [50]. Like the thermal state, the basal topography is difficult to map. In general, the method of choice for improving basal topography data sets is to apply mass conservation constraints based on data assimilation techniques [51] (see the “Data Assimilation Techniques” section). To ensure that basal topography data sets are applicable for long-term simulations with significant ice-front advance, there is a need to extend them outside of the present-day ice extent into the fjords and onto the continental shelf [52]. In places where the subglacial topography is poorly known, it could possibly be improved using a trough-system algorithm [53].
Marine-Terminating Glacier Dynamics
As the GrIS mass loss continues to accelerate [54], most dynamic changes are happening in marine-terminating outlet glaciers, caused by evolution of ice-front positions [55]. Comprehensive treatment of calving processes in large-scale models remains an active field of research. Processes governing calving are complex and include ice properties as well as atmospheric, oceanic and sea ice conditions [56, 57]. The numerical implementation of moving ice fronts in ice flow models is also difficult in unstructured meshes as it requires tracking ice-front positions at sub-element scale and a grid resolution of hundreds of meters [58], which is computationally demanding for continental-scale simulations. Recent developments, relying on the level-set method or linear fracture mechanics, now allow to simulate the evolution of outlet glaciers terminus position [58, 59]. In Greenland, calving is best reproduced using tensile stresses [60], and regional model studies of Jakobshavn Isbræ reproduce the observed acceleration of the glacier over the last three decades when prescribing the ice front evolution [61, 62].
In addition, the interaction of marine-terminating glaciers with ocean water is recognised as an important forcing mechanism, as oceanic conditions impact both submarine melting and calving. However, modelling such interaction remains a challenging problem, mainly due to the large number of poorly mapped fjord geometries, properties of ocean circulation in the fjords and limited observations of melting along ice fronts. In the absence of detailed physically based methods to estimate interactions between outlet glaciers and the ocean explicitly, parameterisations of the bulk effect of the ice-ocean interaction in Greenland fjords have been developed [16, 63]. They represent a simple approach to match model simulations of recent outlet glacier changes to observations and allow projecting the response to both atmospheric and oceanic processes and to estimate the relative importance of the two [16]. The method is a time-dependent extension of an earlier technique that improved the representation of outlet glaciers in a large-scale model with ad hoc adjustment of the sliding relation [64]. More recently, a new empirical discharge parameterisation has been developed [15], with the main goal of improving the simulated extent and margin positions of the ice sheet in a freely evolving model run. Another approach was taken by generalising results from explicit simulations of a limited number of outlet glaciers by a 1D flowline modelling approach [65] and extending the results to the entire ice sheet [66].
Ice Sheet Model Initialisation and Validation
An important driver for recent development in the field of GrIS modelling is improving physically based projections of the ice sheet’s contribution to future sea-level change. Many ice sheet modelling studies build further on the legacy of the SeaRISE [7, 11] and ice2sea [32, 66,69,70,69] projects that provided a set of consistent experiments across models and improved estimates of the ice sheet contribution to sea-level rise for the fifth assessment report of the IPCC [1]. One major conclusion from these projects was the significant impact on centennial ice sheet simulations of differences in model representation of the present-day ice sheets, largely resulting from the initialisation process. Initial ice sheet geometry, velocity structure, basal conditions, englacial properties and imbalance are all critical parameters that should ideally match observations as closely as possible to correctly represent the dynamic state of the ice sheet with confidence. We summarise below the main approaches currently adopted for model initialisation and detail the observations used to validate these models.
Forward Modelling Approaches
Traditionally, long-term modelling approaches including thermodynamic coupling and isostatic bedrock adjustment were used to provide reconstructions of the present-day ice sheet. Using such a spin-up method, an attempt has been recently made to re-examine the SeaRISE experiments (that were difficult to interpret) with one specific model that is systematically perturbed [17]. Results of this study show that differences in the treatment of the SMB calculations and ice sheet initialisation should have the largest impact on the spread of the ice volume changes in the SeaRISE projections. Previous studies comparing initialisation techniques [70, 71] reached similar conclusions concerning the large impact of different methods. These studies [17, 70, 71] all operate with ice sheet models using a forward modelling approach during initialisation, where ice thickness during (part of) the initialisation process is either free to evolve, fixed to the observed or nudged to the observed.
A relatively good match with the observed velocity structure [72, 73] and ice fluxes at the marine margin [74] with such forward model simulations can be achieved without spatially explicit tuning, and results are improved with increasing grid resolution [16]. However, velocity features that are largely caused by local variations in basal conditions that are not related to geometric features like the NEGIS have not been resolved in this type of model based on a freely evolving spin-up. Furthermore, the observed geometry is generally poorly matched without some form of data assimilation, particularly at the margins, where the simulated ice front can be located tens of kilometres away from its present location. This mismatch makes it challenging to properly capture the hypsometry and consequently the mass balance height feedback in future projections. In addition, external SMB products are typically limited to the observed extent, further complicating the simulations if changes in ice-sheet area play a role.
In principle, an almost perfect match with the observed geometry can be achieved with nudging techniques [8, 70, 71] that apply spatially explicit ice flux corrections in places where the modelled ice sheet does not match observations. However, this method has the great disadvantage that the model is not mass conserving, internally inconsistent and exhibits large and rapid drift when the correction is removed [71]. In addition, it falsifies the dynamic response in a forward experiment, as has been shown earlier [66]: the mass fluxes implied by the correction are held constant in time and therefore do not interact with changing ice sheet geometry and boundary conditions. The decisive question when applying this type of method is then how large the correction is in comparison, e.g. with the prescribed SMB or with the mass fluxes at marine-terminating outlet glaciers. Nevertheless, such models may be used successfully for diagnostic velocity solutions, especially at very high spatial resolution [8].
A different approach to improve the match with the observed velocity and geometry consists of allowing for spatially explicit adjustment of model parameters [75], here still in the framework of the forward modelling approach. While regionally optimising the parameters of the positive-degree-day SMB model may largely compensate for deficiencies in the simulated present-day SMB, the improved match with observed velocities in this model [75] is mainly achieved by iteratively updating the applied basal drag coefficients using an inverse method [76]. These methods rely on the concept that the system is fully understood except for one key parameter, in this case the basal coefficient. This parameter is then spatially varied during the initialisation process and arbitrarily held constant in time for projections of future ice sheet evolution. These models therefore capture the overall dynamics of the present-day state, which is not the case with ice sheet models using traditional spin-up techniques.
Data Assimilation Techniques
A second category of techniques relies entirely on observations of the ice sheet. Using observations of ice sheet geometry and assuming the ice rheology (and therefore ice temperature, englacial properties, crystal orientation and impurities) is known, basal friction can be treated as the only unknown parameter. In that case, ice sheet initialisation becomes a time-independent data assimilation problem, with the goal of finding optimal model parameters that minimise the misfit with observations, usually surface velocities [10, 29, 32, 77,80,79]. This approach provides modelled velocities close to observations but causes large unphysical thinning and thickening rates and model drift in forward simulations [29], not as a response to model forcing but as an unphysical response to inconsistencies between data sets. Inconsistencies between the high spatial resolution velocity maps and the low-resolution ice thickness maps, where thickness between observations acquired along flight lines are linearly interpolated, are the main cause of flux divergence anomalies. A model may be relaxed for decades to centuries in order to produce a self-consistent initial state. However, relaxed models may deviate from the target initial conditions and are impacted by the choice of SMB forcing [19, 20, 23, 32, 34].
A new technique to improve basal topography between observations acquired along flight lines was designed, based on the continuity equation and taking advantage of the global coverage in surface velocities [80]. In the mass conservation method [80], ice thickness is first estimated by combining sparse observations of ice thickness with observed surface velocities as well as thinning rates and modelled SMB under the constraint of mass conservation and assuming ice flow is governed by sliding. This multi-parameter optimisation adjusts depth-averaged velocity and apparent mass balance within the observational error in order to minimise the difference between observed and modelled velocities along flight tracks [80]. The method was applied to most outlet glaciers around Greenland [51], allowing significant improvements in the modelling of the velocity fields [8].
The optimisation of the basal topography can also be directly integrated into the data assimilation procedure, either by applying the shallow shelf approximation [35] or a higher-order, non-depth-integrated ice flow model [81]. In the latter, assuming thermomechanical equilibrium with a specified, equilibrium climate forcing, this adjoint-based method combines the misfit with observed surface velocities and ice thickness change in the cost function to be minimised. Combining these different optimisations in a single assimilation procedure allows self-consistency of initial conditions no matter the choice of observations, while models relying on bedrock topography derived with mass conservation should work with observations similar to those used in the optimisation scheme in order to best match observations. However, the combined optimisation typically relies on flux divergence minimisation to adjust bedrock topography [81], which thus does not take advantage of existing thickness measurements and therefore might create unrealistic topographic features.
Instead of only relying on a modelled ice temperature distribution to define the viscosity, one can complement inversion of the basal drag coefficient with an additional optimisation of the stiffness factor [23]. This factor is a parameter in the calculation of the effective viscosity that determines the rheological properties of the ice, which may be dependent on anisotropy, impurities and ice fabric. In this approach, poorly constrained basal and englacial parameters are optimised at the same time, again minimising mismatch of modelled and observed surface velocities. For ice shelves, where there is no unknown basal friction, inversion of ice shelf rheology has been performed to accurately reproduce their flow [29].
As time series of surface elevation and velocity observations become available, a recent development in centennial scale ice sheet modelling concerns techniques that leverage time-dependent observational data sets for data assimilation [34, 82]. The goal in these temporal inversions is to constrain model parameters based on the transient evolution of the system, rather than based on a snapshot or average. It requires a time-dependent adjoint model, typically derived by automatic differentiation [83, 84], which is applicable in principle where observations of sufficient spatial and temporal coverage are available. A working example of temporal inversion exists for the NEGIS [34], where SMB and basal friction are simultaneously optimised using observed changes in surface elevation. A similar method used to calibrate transient projections of a system of outlet glaciers based on surface elevation and velocity observations over a 10-year period has been applied in Antarctica [82]. This approach facilitates study of changes in inferred parameters in time as well as more accurate simulations of the evolution of glaciers’ dynamics. While these methods show great potential for large-scale application, their success will strongly depend on high quality observational data sets becoming available and the capability to scale this approach to large-scale systems.
Another opportunity to improve estimates of ice sheet configuration lies in the recent radar observation of ice isochrones [85] that have been reconstructed and dated over the entire GrIS [86]. These data sets contain invaluable information of the past evolution and conditions of the ice sheet and have the potential to revolutionise reconstructions of the ice sheet state if models are able to integrate all these data [83].
Ice Sheet Model Validation
In order to validate models and assess their reliability, attempts have been made to compare present-day GrIS simulations to remote sensing observations. Comparison with Gravity Recovery and Climate Experiment (GRACE) data [87] for the short period of available observations starting in 2003 [20, 21, 88] highlighted good agreement between modelled and observed mass loss in regions dominated by SMB changes, and lower agreement in areas where dynamic changes are dominant. Given that the GRACE data set is growing and represents a largely independent source of information, complementing the data sets assimilated during initialisation, this exercise has the potential to develop into a powerful evaluation mechanism. Augmented by addition of a comparison with laser altimetry data [89], this procedure has been developed into a complete ice sheet model validation framework [88]. However, the applied ice flow models do not yet incorporate all the processes and forcing to simulate short-term dynamic changes arising from the variability of marine-terminating outlet glaciers and also lack representation of the long-term background evolution arising from past temperature changes [20, 21, 88], implying very large uncertainties. This limits any comparison focused on variability in SMB and ice flow response to recent SMB changes and allows the study of missing short- and long-term dynamical processes only on the basis of residual arguments. The recent acquisition of ice velocity with a high temporal resolution by, e.g., Landsat will improve comparisons of ice dynamics with observations and lead to advances in the representation of physical processes currently lacking in ice flow models.
Interaction with the Climate System
Coupling with the atmosphere in terms of prescribing SMB and temperature boundary conditions in an ice sheet model is common practice and is not further discussed here. Instead, we refer the reader to a review paper on SMB [90]. However, additional challenges come into play when ice sheet models are fully coupled with climate models. A comprehensive review of coupled ice sheet–climate modelling and its challenges dates back to 3 years ago [91], so we only recapitulate some important points here and review the latest developments since then [92,95,96,95]. Two-way coupling requires careful consideration of the exchange of quantities to ensure mass and energy conservation and consistency between the different components. For example, water in solid, liquid and gas form need to be exchanged between ice sheet, climate and ocean models. A tool that facilitates that process is a flexible mapping system [94, 96, 97]. The mapping from one model component to the other is complicated by the need to bridge large differences in the spatial resolution between typically relatively coarse resolution climate models and high-resolution ice sheet models [81]. Recent results with the EC-earth model coupled to an ice sheet model indicate a critical role for the simulation of the surface albedo [95]. Often, the coupling requires downscaling techniques to better represent the SMB boundary condition, critical to achieve a realistic simulation of the ice sheet [92, 93, 95]. One technique is based on energy balance calculations for different elevation classes [92, 93, 98, 99], which allows for correcting the Atmosphere-Ocean General Circulation Model (AOGCM) grid-based results by the elevation difference with the ice sheet grid. This approach exploits the strong relationship between surface elevation and temperature to improve the accuracy of the SMB calculated on the atmospheric grid by downscaling to the ice sheet surface elevation at much higher spatial resolution. Alternatively, local spatial gradients of the SMB can be calculated [100] to directly account for changes in surface elevation in between coupling intervals of AOGCM and ice sheet model or for mismatches in surface elevation. The feedback between the different components of an AOGCM and ice sheet model requires adapted initialisation techniques that take into account differences in the response time of the individual components [101]. Often it is necessary to perform model initialisation of the ice sheet component separately, before coupling with the climate model.
With ISMIP6 [13], fully coupled GCM-ISM modelling has become an integral part of CMIP. In this framework, ad hoc methods to improve the representation of climate boundary conditions (e.g. anomaly forcing or flux correction) are systematically avoided, which may lead to biases in the simulations but guarantees fully physical and clearly interpretable results [13]. This approach appears to be appreciated by most of the fully coupled ice sheet–climate modellers and is an important complement to other methods when attempting to represent the present-day ice sheet as accurately as possible. However, on short time scales, downscaling techniques are unavoidable because of the need of a high spatial resolution for mass balance modelling of the GrIS, which is not yet feasible within full AOGCMs.
Paleo Ice Sheet Simulations
Reconstructing the past evolution of the GrIS may have important implications for our understanding of its present and future behaviour, may provide analogues to the present-day climate and is a challenging scientific endeavour in itself. This is usually done with models representing not only the ice flow itself but also other components of the Earth system (atmosphere, ocean, solid Earth), often in parameterised or simplified form. While the spin-up of paleo-class ice sheet models to incorporate the long-term thermal memory typically covers the last or several glacial–interglacial cycles [15, 16], studying individual periods of the past with a specific focus is its own field of research. From its first inception during the Miocene ~ 10 million years ago [102] to its retreat during the last deglaciation [103], the GrIS has responded to changing climatic boundary conditions. Of particular interest is the GrIS behaviour during past warm periods like the mid Pliocene [104, 105] and the Last Interglacial (LIG) [15, 106,109,110,109], which may bear some resemblance to the expected future warming under anthropogenic greenhouse gas forcing. Once (partially) removed, the re-inception and sustainability of the ice sheet in cooling climatic conditions [109, 110] is of interest in view of potentially similar behaviour during a long-term future decrease of greenhouse gases in the atmosphere.
Sensitivity experiments with different topographic reconstructions were performed to study the conditions during the first inception of the GrIS [102]. The study concludes that growth of the ice sheets is only possible with help of tectonic uplift that produces favourable conditions for ice formation in high-elevation regions. GrIS (re-)inception and sustainability during the Late Pliocene was studied with another ice sheet model forced with GCM climate data under various sensitivity experiments [110]. Albeit operating in the framework of steady-state simulations, the results appear to support the hypothesis that no abrupt inception occurred but rather a cumulative regrowth of the ice sheet during favourable (cold) orbital configurations over several glacial–interglacial cycles.
An intercomparison of ice sheet models forced with simulated climate conditions of the mid-Pliocene warm period [104] indicates strong dependency on the assumed climatic boundary conditions. In contrast, a relative good agreement was found between the participating ice sheet models, which points to a limited sensitivity to ice dynamics. A companion paper complements the work with a study of the influence of several climate models on the response of one particular ice sheet model [105], which underlines the earlier finding and highlights the large uncertainties in climate boundary conditions for this period.
Simulations of the GrIS evolution during the LIG were performed with an ice sheet model asynchronously two-way coupled to a Regional Climate Model [106] to represent the atmospheric boundary condition with high detail. The results indicate a dominance of SMB forcing and a contribution at the lower end of the reported range of the GrIS to the LIG sea-level high-stand [1], suggesting an important contribution of the Antarctic ice sheet to sea level during this period or a possible contribution from Earth dynamics [111]. The importance of insolation forcing for the ice sheet evolution during this period was evaluated and confirmed with a fully coupled ice sheet–climate model of intermediate complexity [107]. Large ensemble simulations were performed for the LIG period and the present day to introduce and evaluate a novel discharge parameterisation [15], which helps to improve the margin position of the ice sheet. For the same period, an Earth system model of intermediate complexity with two-way coupled ice sheet components was used to study the sea-level evolution and ice–climate interactions in one consistent modelling framework [109]. A one-way coupled version of the same model [108] was used to evaluate the impact of ice sheet freshwater fluxes on the climate evolution and suggested a limited influence of GrIS meltwater fluxes in the presence of other, much larger ice sheet changes over Eurasia and North America at the onset of the LIG.
The retreat history of the GrIS during the last deglaciation was reconstructed using an ice sheet model constrained with evidence of past margin positions and relative sea-level indicators [103, 112]. The reconstruction provides important constraints for model spin-up to the present day, when representing the correct loading history and isostatic response.
Given the long-term experiments needed in paleo simulations, ice sheet and climate models and their coupling, are typically treated with reduced resolution and/or reduced complexity for synchronously coupled experiments [107,110,109, 113]. Because of the large contrast in resolution between climate and ice sheet models, the coupling is therefore often done with anomaly methods and/or requires downscaling techniques [113]. However, a continuous increase in the computational resources available to modellers has led to fully coupled AOGCM-ice sheet model simulations slowly becoming feasible for paleo simulations of multi-millennial time scales [114], albeit still with simplified mass balance schemes. It is evident that limitations of GCMs in simulating SMB boundary conditions and in the coupling discussed above for future projections equally apply for paleo applications but may appear less important in the light of other uncertainties arising from, e.g. poorly constrained boundary conditions and forcing in the paleo realm.
Conclusions
We have discussed the literature of recent studies covering overlapping approaches to numerical modelling of the GrIS from paleo applications to future projections. The last few years have seen an important improvement in simulating the present-day dynamic state of the ice sheet, needed as an initial condition for projections of future ice sheet changes. Advances in data assimilation techniques that leverage the growing number of satellite and airborne observations of the ice sheets are at the core of these improvements and have led to modelled ice sheets that reproduce the observed velocity field much better. This is indicative of a growing link between the ice sheet modelling and observational communities, which will also pave the way towards better evaluation and validation mechanisms, which are needed to attach meaningful uncertainty estimates to the projections. However, the relatively short time coverage of satellite data is so far one of the biggest limitations to this effort and further progress is fundamentally dependent on a continuation of high-quality ice sheet observations over time, in order to allow for data assimilation techniques that take advantage of the temporal evolution. A limitation of the current generation of data-assimilated ice sheet models used for short-term projections is the missing representation of long-term processes of the bed response, thermodynamics and a prognostic evolution of the basal conditions. This is complemented by process-based models of long-term ice sheet evolution that typically include these physically based descriptions but often at lower spatial resolution and that exhibit considerable mismatch to the observed geometry and velocity at the present day. Recent development from this side of the modelling spectrum is therefore achieved by a continuous increase in model resolution and simulated detail and by an increasing size of model ensembles used for sensitivity studies and exploring various types of uncertainty.
Two-way coupling between ice sheet models and AOGCMs has seen significant improvements and is on the way to parity in performance with standalone ice sheet models for the goal of performing future projections on multi-centennial time scales. Aside from the intricate complications that arise from coupling two models with dynamic feedbacks between them, one of the main challenges and limitations has long been to produce realistic enough SMB boundary conditions for the ice sheet. Recent development in dynamic downscaling methods has led to an important step forward in this regard.
Paleo studies of GrIS evolution have focused on modelling past warm periods that may help to understand ice sheet behaviour in a warmer than present climate. However, large uncertainties in the climate forcing for the LIG and the mid-Pliocene warm period limit the ability to constrain past ice sheet behaviour and consequently inferences for the long-term future of the ice sheet.
Outlook
Large challenges remain concerning how to combine “the best of both worlds” from long-term spin-up and data assimilation techniques. The goal would be to produce modern ice sheet initial conditions that are close to observations and at the same time include long-term processes like bedrock adjustment and evolving thermodynamics that contain the (thermal) memory of past climate changes. This likely requires joint efforts from different corners of the ice sheet modelling community and integration of time series of observations. A big step in this direction would be to define physically based descriptions of basal processes that could replace the inversion for basal drag by deterministic modelling.
An emerging development that is expected soon is two-way coupling of GrIS models with regional climate models for future projections. Several groups are currently working on what represents an important step forward to explicitly simulate interactions between evolving ice sheet and climate. Direct coupling between ice sheet models and AOGCMs is underway and should over the next few years become available for multi-centennial future projections, on time-scales where ice-climate feedbacks play an important role.
The global ice sheet modelling community has grown significantly in the last several years, leading to new approaches and models with larger user bases. Tighter collaboration between groups across intra-community boundaries should be continued, exemplified by intercomparison exercises like ISMIP6 [13], MISOMIP1 [115] and others, that can lead to standards (e.g., common data formats, application programming interfaces, …) that facilitate further development and model/model-component comparison and validation.
References
Church JA, Clark PU, Cazenave A, Gregory JM, Jevrejeva S, Levermann A, et al. Sea Level Change. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, et al., editors. Climate Change 2013: The Physical Science Basis Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press; 2013. p. 1137–216.
Toniazzo T, Gregory J, Huybrechts P. Climatic impact of a Greenland deglaciation and its possible irreversibility. J Clim. 2004;17(1):21–33.
Ridley J, Gregory JM, Huybrechts P, Lowe J. Thresholds for irreversible decline of the Greenland ice sheet. Clim Dyn. 2010;35(6):1065–73.
Robinson A, Calov R, Ganopolski A. Multistability and critical thresholds of the Greenland ice sheet. Nat Clim Chang. 2012;2(6):429–32.
Rignot E, Xu Y, Menemenlis D, Mouginot J, Scheuchl B, Li X, et al. Modeling of ocean-induced ice melt rates of five west Greenland glaciers over the past two decades. Geophys Res Lett. 2016;43(12):6374–82.
Greve R, Saito F, Abe-Ouchi A. Initial results of the SeaRISE numerical experiments with the models SICOPOLIS and IcIES for the Greenland ice sheet. Ann Glaciol. 2011;52(58):23–30.
Nowicki S, Bindschadler RA, Abe-Ouchi A, Aschwanden A, Bueler E, Choi H, et al. Insights into spatial sensitivities of ice mass response to environmental change from the SeaRISE ice sheet modeling project II: Greenland. J Geophys Res Earth Surf. 2013;118(2):1025–44.
Aschwanden A, Fahnestock MA, Truffer M. Complex Greenland outlet glacier flow captured. Nat Commun. 2016;7:10524.
MacAyeal DR. Large-scale ice flow over a viscous basal sediment: theory and application to ice stream B, Antarctica. J Geophys Res. 1989;94(B4):4071–87.
Joughin I, Fahnestock M, MacAyeal D, Bamber JL, Gogineni P. Observation and analysis of ice flow in the largest Greenland ice stream. J Geophys Res Atmos. 2001;106(D24):34021–34.
Bindschadler RA, Nowicki S, Abe-Ouchi A, Aschwanden A, Choi H, Fastook J, et al. Ice-sheet model sensitivities to environmental forcing and their use in projecting future sea level (the SeaRISE project). J Glaciol. 2013;59(214):195–224.
Goelzer H, Nowicki S, Edwards T, Beckley M, Abe-Ouchi A, Aschwanden A, et al. Design and results of the ice sheet model initialisation experiments initMIP-Greenland: an ISMIP6 intercomparison. Cryosphere Discuss. 2017;2017:1–42.
Nowicki SMJ, Payne A, Larour E, Seroussi H, Goelzer H, Lipscomb W, et al. Ice Sheet Model Intercomparison Project (ISMIP6) contribution to CMIP6. Geosci Model Dev. 2016;9(12):4521–45.
Pattyn F, Favier L, Sun S, Durand G. Progress in numerical modeling of Antarctic ice-sheet dynamics. Curr Clim Chang Rep. 2017;3(3):174–84.
Calov R, Robinson A, Perrette M, Ganopolski A. Simulating the Greenland ice sheet under present-day and palaeo constraints including a new discharge parameterization. The Cryosphere. 2015;9(1):179–96.
Fürst JJ, Goelzer H, Huybrechts P. Ice-dynamic projections of the Greenland ice sheet in response to atmospheric and oceanic warming. The Cryosphere. 2015;9:1039–62.
Saito F, Abe-Ouchi A, Takahashi K, Blatter H. SeaRISE experiments revisited: potential sources of spread in multi-model projections of the Greenland ice sheet. The Cryosphere. 2016;10(1):43–63.
Seroussi H, Morlighem M, Rignot E, Khazendar A, Larour E, Mouginot J. Dependence of century-scale projections of the Greenland ice sheet on its thermal regime. J Glaciol. 2013;59(218):1024–34.
Schlegel NJ, Larour E, Seroussi H, Morlighem M, Box JE. Ice discharge uncertainties in Northeast Greenland from boundary conditions and climate forcing of an ice flow model. J Geophys Res Earth. 2015;120(1):29–54.
Schlegel NJ, Wiese DN, Larour EY, Watkins MM, Box JE, Fettweis X, et al. Application of GRACE to the assessment of model-based estimates of monthly Greenland Ice Sheet mass balance (2003–2012). The Cryosphere. 2016;10(5):1965–89.
Alexander PM, Tedesco M, Schlegel NJ, Luthcke SB, Fettweis X, Larour E. Greenland Ice Sheet seasonal and spatial mass variability from model simulations and GRACE (2003–2012). The Cryosphere. 2016;10(3):1259–77.
Cornford SL, Martin DF, Graves DT, Ranken DF, Le Brocq AM, Gladstone RM, et al. Adaptive mesh, finite volume modeling of marine ice sheets. J Comput Phys. 2013;232(1):529–49.
Lee V, Cornford SL, Payne AJ. Initialization of an ice-sheet model for present-day Greenland. Ann Glaciol. 2015;56(70):129–40.
Schoof C, Hewitt I. Ice-sheet dynamics. Annu Rev Fluid Mech. 2013;45:217–39.
Greve R. Application of a polythermal three-dimensional ice sheet model to the Greenland ice sheet: response to steady-state and transient climate scenarios. J Clim. 1997;10(5):901–18.
Hindmarsh RCA. A numerical comparison of approximations to the Stokes equations used in ice sheet and glacier modeling. J Geophys Res Earth Surf. 2004;109(F1):F01012.
Schoof C, Hindmarsh RCA. Thin-film flows with wall slip: an asymptotic analysis of higher order glacier flow models. Q J Mech Appl Math. 2010;63(1):73–114.
Bueler E, Brown J. Shallow shelf approximation as a “sliding law” in a thermomechanically coupled ice sheet model. J Geophys Res. 2009;114(F3):F03008.
Seroussi H, Morlighem M, Rignot E, Larour E, Aubry D, Ben Dhia H, et al. Ice flux divergence anomalies on 79north Glacier, Greenland. Geophys Res Lett. 2011;38(9):L09501.
Ahlkrona J, Lötstedt P, Kirchner N, Zwinger T. Dynamically coupling the non-linear Stokes equations with the shallow ice approximation in glaciology: description and first applications of the ISCAL method. J Comput Phys. 2016;308:1–19.
Seddik H, Greve R, Zwinger T, Gillet-Chaulet F, Gagliardini O. Simulations of the Greenland ice sheet 100 years into the future with the full Stokes model Elmer/Ice. J Glaciol. 2012;58(209):427–40.
Gillet-Chaulet F, Gagliardini O, Seddik H, Nodet M, Durand G, Ritz C, et al. Greenland ice sheet contribution to sea-level rise from a new-generation ice-sheet model. The Cryosphere. 2012;6:1561–76.
Bernales J, Rogozhina I, Greve R, Thomas M. Comparison of hybrid schemes for the combination of shallow approximations in numerical simulations of the Antarctic Ice Sheet. The Cryosphere. 2017;11(1):247–65.
Larour E, Utke J, Csatho B, Schenk A, Seroussi H, Morlighem M, et al. Inferred basal friction and surface mass balance of the Northeast Greenland Ice Stream using data assimilation of ICESat (Ice Cloud and land Elevation Satellite) surface altimetry and ISSM (Ice Sheet System Model). The Cryosphere. 2014;8(6):2335–51.
Mosbeux C, Gillet-Chaulet F, Gagliardini O. Comparison of adjoint and nudging methods to initialise ice sheet model basal conditions. Geosci Model Dev. 2016;9(7):2549–62.
Aschwanden A, Bueler E, Khroulev C, Blatter H. An enthalpy formulation for glaciers and ice sheets. J Glaciol. 2012;58(209):441–57.
Lliboutry L, Duval P. Various isotropic and anisotropic ices found in glaciers and polar ice caps and their corresponding rheologies. Ann Geophys. 1985;3(2):207–24.
Lüthi MP, Ryser C, Andrews LC, Catania GA, Funk M, Hawley RL, et al. Heat sources within the Greenland Ice Sheet: dissipation, temperate paleo-firn and cryo-hydrologic warming. The Cryosphere. 2015;9(1):245–53.
Phillips T, Rajaram H, Steffen K. A potential mechanism for rapid thermal response of ice sheets. Geophys Res Lett. 2010;37:L20503.
Glen JW. The creep of polycrystalline ice. Proc R Soc London, Ser B. 1955;228:519–38.
Montagnat M, Azuma N, Dahl-Jensen D, Eichler J, Fujita S, Gillet-Chaulet F, et al. Fabric along the NEEM ice core, Greenland, and its comparison with GRIP and NGRIP ice cores. The Cryosphere. 2014;8(4):1129–38.
Gillet-Chaulet F, Hindmarsh RCA, Corr HFJ, King EC, Jenkins A. In-situ quantification of ice rheology and direct measurement of the Raymond Effect at Summit, Greenland using a phase-sensitive radar. Geophys Res Lett. 2011;38(24):L24503.
Bons PD, Jansen D, Mundel F, Bauer CC, Binder T, Eisen O, et al. Converging flow and anisotropy cause large-scale folding in Greenland's ice sheet. Nat Commun. 2016;7:11427.
Meierbachtol TW, Harper JT, Johnson JV, Humphrey NF, Brinkerhoff DJ. Thermal boundary conditions on western Greenland: observational constraints and impacts on the modeled thermomechanical state. J Geophys Res-Earth. 2015;120(3):623–36.
Rogozhina I, Petrunin AG, Vaughan APM, Steinberger B, Johnson JV, Kaban MK, et al. Melting at the base of the Greenland ice sheet explained by Iceland hotspot history. Nat Geosci. 2016;9(5):366–9.
Colgan W, Sommers A, Rajaram H, Abdalati W, Frahm J. Considering thermal-viscous collapse of the Greenland ice sheet. Earth Futur. 2015;3(7):252–67.
Nienow PW, Sole AJ, Slater DA, Cowton TR. Greenland - the role of meltwater in the ice sheet system. Current Climate Change Reports. 2017, accepted.
Krabbendam M. Sliding of temperate basal ice on a rough, hard bed: creep mechanisms, pressure melting, and implications for ice streaming. The Cryosphere. 2016;10(4):1915–32.
MacGregor JA, Fahnestock MA, Catania GA, Aschwanden A, Clow GD, Colgan WT, et al. A synthesis of the basal thermal state of the Greenland Ice Sheet. J Geophys Res Earth Surf. 2016;121(7):1328–50.
Carr JR, Vieli A, Stokes CR, Jamieson SSR, Palmer SJ, Christoffersen P, et al. Basal topographic controls on rapid retreat of Humboldt Glacier, northern Greenland. J Glaciol. 2015;61(225):137–50.
Morlighem M, Rignot E, Mouginot J, Seroussi H, Larour E. Deeply incised submarine glacial valleys beneath the Greenland ice sheet. Nat Geosci. 2014;7(6):418–22.
Morlighem M, Rignot E, Willis JK. Improving bed topography mapping of Greenland glaciers using NASA’s Oceans Melting Greenland (OMG) data. Oceanography. 2016;29(4):62–71.
Herzfeld UC, McDonald BW, Wallin BF, Chen PA, Mayer H, Paden J, et al. The trough-system algorithm and its application to spatial modeling of Greenland subglacial topography. Ann Glaciol. 2014;55(67):115–26.
Enderlin EM, Howat IM, Jeong S, Noh M-J, van Angelen JH, van den Broeke MR. An improved mass budget for the Greenland ice sheet. Geophys Res Lett. 2014;41(3):866–72.
Moon T, Joughin I, Smith B. Seasonal to multiyear variability of glacier surface velocity, terminus position, and sea ice/ice mélange in northwest Greenland. J Geophys Res Earth Surf. 2015;120(5):818–33.
Benn DI, Warren CR, Mottram RH. Calving processes and the dynamics of calving glaciers. Earth Sci Rev. 2007;82(3):143–79.
Benn DI, Cowton T, Todd J, Luckman A. Glacier calving in Greenland. Current Climate Change Reports. 2017, accepted.
Bondzio JH, Seroussi H, Morlighem M, Kleiner T, Rückamp M, Humbert A, et al. Modelling calving front dynamics using a level-set method: application to Jakobshavn Isbræ, West Greenland. Cryosphere. 2016;10(2):497–510.
Krug J, Weiss J, Gagliardini O, Durand G. Combining damage and fracture mechanics to model calving. The Cryosphere. 2014;8(6):2101–17.
Morlighem M, Bondzio J, Seroussi H, Rignot E, Larour E, Humbert A, et al. Modeling of Store Gletscher's calving dynamics, West Greenland, in response to ocean thermal forcing. Geophys Res Lett. 2016;43(6):2659–66.
Muresan IS, Khan SA, Aschwanden A, Khroulev C, Van Dam T, Bamber J, et al. Modelled glacier dynamics over the last quarter of a century at Jakobshavn Isbræ. The Cryosphere. 2016;10(2):597–611.
Bondzio JH, Morlighem M, Seroussi H, Kleiner T, Rückamp M, Mouginot J, et al. The mechanisms behind Jakobshavn Isbræ’s acceleration and mass loss: a 3-D thermomechanical model study. Geophys Res Lett. 2017;44(12):6252–60.
Price SF, Payne AJ, Howat IM, Smith BE. Committed sea-level rise for the next century from Greenland ice sheet dynamics during the past decade. Proc Natl Acad Sci U S A. 2011;108(22):8978–83.
Graversen RG, Drijfhout S, Hazeleger W, van de Wal R, Bintanja R, Helsen M. Greenland’s contribution to global sea-level rise by the end of the 21st century. Clim Dyn. 2011;37(7):1427–42.
Nick FM, Vieli A, Andersen ML, Joughin I, Payne A, Edwards TL, et al. Future sea-level rise from Greenland/'s main outlet glaciers in a warming climate. Nature. 2013;497(7448):235–8.
Goelzer H, Huybrechts P, Fürst JJ, Andersen ML, Edwards TL, Fettweis X, et al. Sensitivity of Greenland ice sheet projections to model formulations. J Glaciol. 2013;59(216):733–49.
Shannon SR, Payne AJ, Bartholomew ID, van den Broeke MR, Edwards TL, Fettweis X, et al. Enhanced basal lubrication and the contribution of the Greenland ice sheet to future sea level rise. Proc Natl Acad Sci U S A. 2013;110(35):14156–61.
Edwards TL, Fettweis X, Gagliardini O, Gillet-Chaulet F, Goelzer H, Gregory JM, et al. Effect of uncertainty in surface mass balance–elevation feedback on projections of the future sea level contribution of the Greenland ice sheet. The Cryosphere. 2014;8(1):195–208.
Edwards TL, Fettweis X, Gagliardini O, Gillet-Chaulet F, Goelzer H, Gregory JM, et al. Probabilistic parameterisation of the surface mass balance–elevation feedback in regional climate model simulations of the Greenland ice sheet. The Cryosphere. 2014;8(1):181–94.
Aschwanden A, Aðalgeirsdóttir G, Khroulev C. Hindcasting to measure ice sheet model sensitivity to initial states. The Cryosphere. 2013;7(4):1083–93.
Adalgeirsdottir G, Aschwanden A, Khroulev C, Boberg F, Mottram R, Lucas-Picher P, et al. Role of model initialization for projections of 21st-century Greenland ice sheet mass loss. J Glaciol. 2014;60(222):782–94.
Joughin I, Smith BE, Howat IM, Scambos T, Moon T. Greenland flow variability from ice-sheet-wide velocity mapping. J Glaciol. 2010;56(197):415–30.
Rignot E, Mouginot J. Ice flow in Greenland for the International Polar Year 2008–2009. Geophys Res Lett. 2012;39(11).
Rignot E, Kanagaratnam P. Changes in the velocity structure of the Greenland ice sheet. Science. 2006;311(5763):986–90.
Peano D, Colleoni F, Quiquet A, Masina S. Ice flux evolution in fast flowing areas of the Greenland ice sheet over the 20th and 21st centuries. J Glaciol. 2017;63(239):499–513.
Pollard D, DeConto RM. A simple inverse method for the distribution of basal sliding coefficients under ice sheets, applied to Antarctica. The Cryosphere. 2012;6(5):953–71.
MacAyeal DR. A tutorial on the use of control methods in ice-sheet modeling. J Glaciol. 1993;39(131):91–8.
Morlighem M, Rignot E, Seroussi H, Larour E, Ben Dhia H, Aubry D. Spatial patterns of basal drag inferred using control methods from a full-Stokes and simpler models for Pine Island Glacier, West Antarctica. Geophys Res Lett. 2010;37(14):L14502.
Larour E, Seroussi H, Morlighem M, Rignot E. Continental scale, high order, high spatial resolution, ice sheet modeling using the Ice Sheet System Model (ISSM). J Geophys Res. 2012;117(F1).
Morlighem M, Rignot E, Seroussi H, Larour E, Ben Dhia H, Aubry D. A mass conservation approach for mapping glacier ice thickness. Geophys Res Lett. 2011;38(19).
Perego M, Price S, Stadler G. Optimal initial conditions for coupling ice sheet models to Earth system models. J Geophys Res Earth. 2014;119(9):1894–917.
Goldberg DN, Heimbach P, Joughin I, Smith B. Committed retreat of Smith, Pope, and Kohler Glaciers over the next 30 years inferred by transient model calibration. The Cryosphere. 2015;9(6):2429–46.
Goldberg DN, Heimbach P. Parameter and state estimation with a time-dependent adjoint marine ice sheet model. The Cryosphere. 2013;7(6):1659–78.
Larour E, Utke J, Bovin A, Morlighem M, Perez G. An approach to computing discrete adjoints for MPI-parallelized models applied to Ice Sheet System Model 4.11. Geosci Model Dev. 2016;9(11):3907–18.
Sime LC, Karlsson NB, Paden JD, Prasad GS. Isochronous information in a Greenland ice sheet radio echo sounding data set. Geophys Res Lett. 2014;41(5):1593–9.
MacGregor JA, Fahnestock MA, Catania GA, Paden JD, Prasad Gogineni S, Young SK, et al. Radiostratigraphy and age structure of the Greenland Ice Sheet. J Geophys Res Earth Surf. 2015;120(2):212–41.
Watkins MM, Wiese DN, Yuan D-N, Boening C, Landerer FW. Improved methods for observing Earth's time variable mass distribution with GRACE using spherical cap mascons. J Geophys Res Earth Surf. 2015;120(4):2648–71.
Price SF, Hoffman MJ, Bonin JA, Howat IM, Neumann T, Saba J, et al. An ice sheet model validation framework for the Greenland ice sheet. Geosci Model Dev. 2017;10(1):255–70.
Zwally HJ, Schutz B, Abdalati W, Abshire J, Bentley C, Brenner A, et al. ICESat's laser measurements of polar ice, atmosphere, ocean, and land. J Geodyn. 2002;34(3–4):405–45.
van den Broeke M, Box J, Fettweis X, Hanna E, Noël B, Tedesco M et al. Greenland ice sheet surface mass loss: recent developments in observation and modelling. Current Climate Change Reports. 2017, accepted.
Vizcaino M. Ice sheets as interactive components of Earth System Models: progress and challenges. Wiley Interdiscip Rev Clim Chang. 2014;5(4):557–68.
Fyke J, Eby M, Mackintosh A, Weaver A. Impact of climate sensitivity and polar amplification on projections of Greenland Ice Sheet loss. Clim Dyn. 2014;43(7):2249–60.
Vizcaino M, Mikolajewicz U, Ziemen F, Rodehacke CB, Greve R, van den Broeke MR. Coupled simulations of Greenland Ice Sheet and climate change up to AD 2300. Geophys Res Lett. 2015;42(10):3927–35.
Reerink TJ, van de Berg WJ, van de Wal RSW. OBLIMAP 2.0: a fast climate model–ice sheet model coupler including online embeddable mapping routines. Geosci Model Dev. 2016;9(11):4111–32.
Helsen MM, van de Wal RSW, Reerink TJ, Bintanja R, Madsen MS, Yang S, et al. On the importance of the albedo parameterization for the mass balance of the Greenland ice sheet in EC-Earth. The Cryosphere. 2017;11(4):1949–65.
Reerink TJ, Kliphuis MA, van de Wal RSW. Mapping technique of climate fields between GCM's and ice models. Geosci Model Dev. 2010;3(1):13–41.
Fischer R, Nowicki S, Kelley M, Schmidt GA. A system of conservative regridding for ice-atmosphere coupling in a General Circulation Model (GCM). Geosci Model Dev. 2014;7(3):883–907.
Fyke JG, Weaver AJ, Pollard D, Eby M, Carter L, Mackintosh A. A new coupled ice sheet/climate model: description and sensitivity to model physics under Eemian, Last Glacial Maximum, late Holocene and modern climate conditions. Geosci Model Dev. 2011;4(1):117–36.
Lipscomb WH, Fyke JG, Vizcaíno M, Sacks WJ, Wolfe J, Vertenstein M, et al. Implementation and initial evaluation of the Glimmer Community Ice Sheet Model in the Community Earth System Model. J Clim. 2013;26(19):7352–71.
Helsen MM, van de Wal RSW, van den Broeke MR, van de Berg WJ, Oerlemans J. Coupling of climate models and ice sheet models by surface mass balance gradients: application to the Greenland Ice Sheet. The Cryosphere. 2012;6(2):255–72.
Fyke JG, Sacks WJ, Lipscomb WH. A technique for generating consistent ice sheet initial conditions for coupled ice sheet/climate models. Geosci Model Dev. 2014;7(3):1183–95.
Solgaard AM, Bonow JM, Langen PL, Japsen P, Hvidberg CS. Mountain building and the initiation of the Greenland Ice Sheet. Palaeogeogr Palaeoclimatol Palaeoecol. 2013;392:161–76.
Lecavalier BS, Milne GA, Simpson MJR, Wake L, Huybrechts P, Tarasov L, et al. A model of Greenland ice sheet deglaciation constrained by observations of relative sea level and ice extent. Quat Sci Rev. 2014;102:54–84.
Koenig SJ, Dolan AM, de Boer B, Stone EJ, Hill DJ, DeConto RM, et al. Ice sheet model dependency of the simulated Greenland Ice Sheet in the mid-Pliocene. Clim Past. 2015;11(3):369–81.
Dolan AM, Hunter SJ, Hill DJ, Haywood AM, Koenig SJ, Otto-Bliesner BL, et al. Using results from the PlioMIP ensemble to investigate the Greenland Ice Sheet during the mid-Pliocene Warm Period. Clim Past. 2015;11(3):403–24.
Helsen MM, van de Berg WJ, van de Wal RSW, van den Broeke MR, Oerlemans J. Coupled regional climate-ice-sheet simulation shows limited Greenland ice loss during the Eemian. Clim Past. 2013;9(4):1773–88.
Robinson A, Goelzer H. The importance of insolation changes for paleo ice sheet modeling. The Cryosphere. 2014;8(1):1419–28.
Goelzer H, Huybrechts P, Loutre MF, Fichefet T. Impact of ice sheet meltwater fluxes on the climate evolution at the onset of the Last Interglacial. Clim Past. 2016;12(8):1721–37.
Goelzer H, Huybrechts P, Loutre MF, Fichefet T. Last Interglacial climate and sea-level evolution from a coupled ice sheet–climate model. Clim Past. 2016;12(12):2195–213.
Contoux C, Dumas C, Ramstein G, Jost A, Dolan AM. Modelling Greenland ice sheet inception and sustainability during the Late Pliocene. Earth Planet Sci Lett. 2015;424:295–305.
Austermann J, Mitrovica JX, Huybers P, Rovere A. Detection of a dynamic topography signal in last interglacial sea-level records. Science Advances. 2017;3(7).
Lecavalier BS. A Holocene temperature record from the Agassiz ice cap: implications for high-Arctic climate change and Greenland ice sheet evolution. Proc Natl Acad Sci U S A. 2017;114(23):5952–7.
Roche DM, Dumas C, Bügelmayer M, Charbit S, Ritz C. Adding a dynamical cryosphere to iLOVECLIM (version 1.0): coupling with the GRISLI ice-sheet model. Geosci Model Dev. 2014;7(4):1377–94.
Ziemen FA, Rodehacke CB, Mikolajewicz U. Coupled ice sheet–climate modeling under glacial and pre-industrial boundary conditions. Clim Past. 2014;10(5):1817–36.
Asay-Davis XS, Cornford SL, Durand G, Galton-Fenzi BK, Gladstone RM, Gudmundsson GH, et al. Experimental design for three interrelated marine ice sheet and ocean model intercomparison projects: MISMIP v. 3 (MISMIP +), ISOMIP v. 2 (ISOMIP +) and MISOMIP v. 1 (MISOMIP1). Geosci Model Dev. 2016;9(7):2471–97.
Acknowledgements
H. Goelzer has received funding from the program of the Netherlands Earth System Science Centre (NESSC), financially supported by the Dutch Ministry of Education, Culture and Science (OCW) under Grant No. 024.002.001. A. Robinson is funded by the Marie Curie Horizon2020 project CONCLIMA (Grant No. 703251). H. Seroussi is funded by the NASA Cryospheric Science Program. We would like to thank two anonymous reviewers for valuable comments on the manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
This article is part of the Topical Collection on Glaciology and Climate Change
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Goelzer, H., Robinson, A., Seroussi, H. et al. Recent Progress in Greenland Ice Sheet Modelling. Curr Clim Change Rep 3, 291–302 (2017). https://doi.org/10.1007/s40641-017-0073-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40641-017-0073-y