Skip to main content
SpringerLink
Log in

Local maximum likelihood segmentation of echocardiographic images with Rayleigh distribution

  • Original Paper
  • Published:
Signal, Image and Video Processing Aims and scope Submit manuscript

Abstract

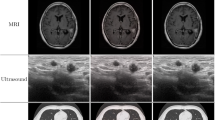
In order to interpret ultrasound images, it is important to understand their formation and the properties that affect them, especially speckle noise. This image texture, or speckle, is a correlated and multiplicative noise that inherently occurs in all types of coherent imaging systems. Indeed, its statistics depend on the density and on the type of scatterers in the tissues. This paper presents a new method for echocardiographic images segmentation in a variational level set framework. A partial differential equation-based flow is designed locally in order to achieve a maximum likelihood segmentation of the region of interest. A Rayleigh probability distribution is considered to model the local B-mode ultrasound images intensities. In order to confront more the speckle noise and local changes of intensity, the proposed local region term is combined with a local phase-based geodesic active contours term. Comparison results on natural and simulated images show that the proposed model is robust to attenuations and captures well the low-contrast boundaries.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Ahn, C.Y., Jung, Y.M., Kwon, O.I., Seo, J.K.: Fast segmentation of ultrasound images using robust Rayleigh distribution decomposition. Pattern Recognit. 45(9), 3490–3500 (2012)

    Article  MATH  Google Scholar 

  2. Alessandrini, M., Basarab, A., Liebgott, H., Bernard, O.: Myocardial motion estimation from medical images using the monogenic signal. IEEE Trans. Image Process. 22(3), 1084–1095 (2013). https://doi.org/10.1109/TIP.2012.2226903

    Article  MathSciNet  MATH  Google Scholar 

  3. Belaid, A., Boukerroui, D.: \(\alpha \) scale spaces filters for phase based edge detection in ultrasound images. In: IEEE International Symposium on Biomedical Imaging, pp. 1247–1250. Beijing, China (2014)

  4. Belaid, A., Boukerroui, D.: A new generalised \(\alpha \) scale spaces quadrature filters. Pattern Recognit. 47(10), 3209–3224 (2014)

    Article  MATH  Google Scholar 

  5. Belaid, A., Boukerroui, D., Maingourd, Y., Lerallut, J.F.: Implicit active contours for ultrasound images segmentation driven by phase information and local maximum likelihood, pp. 630–635. Chicago, IL, USA (2011)

  6. Belaid, A., Boukerroui, D., Maingourd, Y., Lerallut, J.F.: Phase based level set segmentation of ultrasound images. IEEE Trans. Inf. Technol. Biomed. 15(1), 138–147 (2011)

    Article  Google Scholar 

  7. Bosch, J., Mitchell, S., Lelieveldt, B.P., Nijland, F., Kamp, O., Sonka, M., Reiber, J.H.: Automatic segmentation of echocardiographic sequences by active appearance motion models. IEEE Trans. Med. Imaging 21(11), 1373–1383 (2002)

    Article  Google Scholar 

  8. Boukerroui, D.: A local Rayleigh model with spatial scale selection for ultrasound image segmentation. In: British Machine Vision Conference, BMVC 2012, Surrey, UK, September 3–7, 2012, pp. 1–12 (2012)

  9. Boukerroui, D., Baskurt, A., Noble, J.A., Basset, O.: Segmentation of ultrasound images: multiresolution 2D and 3D algorithm based on global and local statistics. Pattern Recognit. Lett. 24(4–5), 779–790 (2003)

    Article  Google Scholar 

  10. Boukerroui, D., Noble, J.A., Robini, M.C., Brady, J.: Enhancement of contrast regions in sub-optimal ultrasound images with application to echocardiography. Ultrasound Med. Biol. 27(12), 1583–1594 (2001)

    Article  Google Scholar 

  11. Brox, T., Cremers, D.: On local region models and a statistical interpretation of the piecewise smooth mumford-shah functional. Int. J. Comput. Vis. 84(2), 184–193 (2009)

    Article  Google Scholar 

  12. Chesnaud, C., Refregier, P., Boulet, V.: Statistical region snake-based segmentation adapted to different physical noise models. IEEE Trans. Pattern Anal. Mach. Intell. 21(11), 1145–1157 (1999)

    Article  Google Scholar 

  13. Caselles, V., Kimmel, R., Sapiro, G.: Geodesic active contours. Int. J. Comput. Vis. 22(1), 61–79 (1997)

    Article  MATH  Google Scholar 

  14. Chalana, V., Linker, D.T., Haynor, D.R., Kim, Y.: A multiple active contour model for cardiac boundary detection on echocardiographic sequences. IEEE Trans. Med. Imaging 15(3), 290–298 (1996)

    Article  Google Scholar 

  15. Cootes, T.F., Taylor, C.J., Cooper, D.H., Graham, J.: Active shape models—their training and application. Comput. Vis. Image Underst. 61(1), 38–59 (1995)

    Article  Google Scholar 

  16. Cremers, D., Rousson, M., Deriche, R.: A review of statistical approaches to level set segmentation: integrating color, texture, motion and shape. Int. J. Comput. Vis. 72(2), 195–215 (2007)

    Article  Google Scholar 

  17. Dietenbeck, T., Alessandrini, M., Barbosa, C., D’Hooge, J., Friboulet, D., Bernard, O.: Detection of the whole myocardium in 2D-echocardiography for multiple orientations using a geometrically constrained level-set. Med. Image Anal. 16(2), 386–401 (2012). https://doi.org/10.1016/j.media.2011.10.003

    Article  Google Scholar 

  18. Drukker, K., Giger, M.L., Mendelson, E.B.: Computerized detection and classification of cancer on breast ultrasound. Acad. Radiol. 11(5), 526–535 (2004)

    Article  Google Scholar 

  19. Dutt, V., Greenleaf, J.F.: Ultrasound echo envelope analysis using a homodyned K distribution signal model. Ultrason. Imaging 16(4), 265–287 (1994)

    Article  Google Scholar 

  20. Eltoft, T.: The Rician inverse gaussian distribution: a new model for non-rayleigh signal amplitude statistics. IEEE Trans. Image Process. 14(11), 1722–1735 (2005)

    Article  MathSciNet  Google Scholar 

  21. Felsberg, M., Sommer, G.: The monogenic signal. IEEE Trans. Signal Process. 49(49), 3136–3144 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  22. Felsberg, M., Sommer, G.: The monogenic scale-space: a unifying approach to phase-based image processing in scale-space. J. Math. Imaging Vis. 21(1), 5–26 (2004)

    Article  MathSciNet  Google Scholar 

  23. Fernandes, D., Sekine, M.: Suppression of Weibull radar clutter. IEICE Trans. Commun. E76–B, 1231–1235 (1993)

    Google Scholar 

  24. Heimann, T., Meinzer, H.P.: Statistical shape models for 3D medical image segmentation: a review. Med. Image Anal. 13(4), 543–563 (2009)

    Article  Google Scholar 

  25. Jacob, G., Noble, J., Behrenbruch, C., Kelion, A., Banning, A.: A shape-space-based approach to tracking myocardial borders and quantifying regional left-ventricular function applied in echocardiography. IEEE Trans. Med. Imaging 21(3), 226–238 (2002)

    Article  Google Scholar 

  26. Jardim, S., Figueiredo, M.: Segmentation of fetal ultrasound images. Ultrasound Med. Biol. 31(2), 243–250 (2005)

    Article  Google Scholar 

  27. Jensen, J.A.,: Field: a program for simulating ultrasound systems In: 10th Nordic-Baltic Conference on Biomedical Imaging, vol .34, pp. 351–353 (1996)

  28. Kovesi, P.: Image features from phase congruency. Videre J. Comput. Vis. Res. 1(3), 1–26 (1999)

    Google Scholar 

  29. Lankton, S., Tannenbaum, A.: Localizing region-based active contours. IEEE Trans. Image Process. 17(11), 2029–2039 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  30. Li, C., Kao, C., Gore, J., Ding, Z.: Implicit active contours driven by local binary fitting energy. In: Proceedings of IEEE Conference on Computer Vision Pattern Recognition (CVPR), pp. 1–7. IEEE Computer Society, Washington (2007)

  31. Lin, N., Yu, W., Duncan, J.S.: Combinative multi-scale level set framework for echocardiographic image segmentation. Med. Image Anal. 7, 529–537 (2003)

    Article  MATH  Google Scholar 

  32. Martin-Fernandez, M., Alberola-Lopez, C.: An approach for contour detection of human kidneys from ultrasound images using markov random fields and active contours. Med. Image Anal. 9(1), 21–23 (2005)

    Google Scholar 

  33. Mignotte, M., Collet, C., Pérez, P., Bouthemy, P.: Three-class Markovian segmentation of high-resolution sonar images. CVIU 76(3), 191–204 (1999)

    Google Scholar 

  34. Morrone, M.C., Burr, D.C.: Feature detection in human vision: a phase-dependent energy model. In: Proceedings of the Royal Society of London, Series B, vol. 235, pp. 221–245 (1988)

  35. Mulet-Parada, M., Noble, J.A.: 2D+T acoustic boundary detection in echocardiography. In: MICCAI, pp. 806–813. Springer, London (1998)

  36. Mulet-Parada, M., Noble, J.A.: 2D+ T acoustic boundary detection in echocardiography. Med. Image Anal. 4(1), 21–30 (2000)

    Article  Google Scholar 

  37. Noble, J.A.: Ultrasound image segmentation and tissue characterization. Proc. IMechE H J. Eng. Med. 224(2), 307–316 (2010)

    Article  Google Scholar 

  38. Noble, J.A., Boukerroui, D.: Ultrasound image segmentation: a survey. IEEE Trans. Med. Imaging 25(8), 987–1010 (2006)

    Article  Google Scholar 

  39. Papadogiorgaki, M., Mezaris, V., Chatzizisis, Y.S., Giannoglou, G.D., Kompatsiaris, I.: Image analysis techniques for automated IVUS contour detection. Ultrasound Med. Biol. 34(9), 1482–1498 (2008)

    Article  Google Scholar 

  40. Paragios, N., Jolly, M.P., Taron, M., Ramaraj, R.: Active shape models & segmentation of the left ventricle in echocardiography. In: International Conference on Scale Space Theories and PDEs methods in Computer Vision. Lecture Notes in Computer Science, vol. 3459, pp. 131–142 (2005)

  41. Porras, A., Alessandrini, M., De Craene, M., Duchateau, N., Sitges, M., Bijnens, B., Delingette, H., Sermesant, M., D’Hooge, J., Frangi, A., Piella, G.: Improved myocardial motion estimation combining tissue Doppler and B-mode echocardiographic images. IEEE Trans. Med. Imaging 33(11), 2098–2106 (2014). https://doi.org/10.1109/TMI.2014.2331392

    Article  Google Scholar 

  42. Raju, B.I., Srinivasan, M.A.: Statistics of envelope of high-frequency ultrasonic backscatter from human skin in vivo. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 49(6), 871–882 (2002)

    Article  Google Scholar 

  43. Roy, S., Carass, A., Bazin, P.L., Resnick, S., Prince, J.L.: Consistent segmentation using a Rician classifier. Med. Image Anal. 16(6), 524–535 (2012)

    Article  Google Scholar 

  44. Sarti, A., Corsi, C., Mazzini, E., Lamberti, C.: Maximum likelihood segmentation of ultrasound images with Rayleigh distribution. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 52(6), 947–960 (2005)

    Article  Google Scholar 

  45. Shankar, P.M.: A general statistical model for ultrasonic backscattering from tissues. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 47(6), 727–736 (2000)

    Article  Google Scholar 

  46. Slabaugh, G., Unal, G., Wels, M., Fang, T., Rao, B.: Statistical region-based segmentation of ultrasound images. Ultrasound Med. Biol. 35(5), 781–795 (2009)

    Article  Google Scholar 

  47. Steen, E., Olstad, B.: Scale-space and boundary detection in ultrasonic imaging using nonlinear signal-adaptive anisotropic diffusion. In: Proceedings of SPIE Medical Imaging: Image processing (1994)

  48. Song, Z., Awate, S.P., Licht, D.J., Gee J.C. :Clinical neonatal brain MRI segmentation using adaptive nonparametric data models and intensity-based Markov priors. In: Proceedings of Medical Image Computing and Computer Assisted Intervention, pp. 883-890 (2007)

  49. Tao, Z., Tagare, H.: Tunneling descent level set segmentation of ultrasound images. In: IPMI, pp. 750–761 (2005)

  50. Tohka, J., Dinov, I.D., Shattuck, D.W., Toga, A.W.: Brain MRI tissue classification based on local Markov random fields. Magn. Reson. Imaging 28(11), 557–573 (2010)

    Article  Google Scholar 

  51. Wang, L., He, L., Mishra, A., Li, C.: Active contours driven by local gaussian distribution fitting energy. Signal Process. 89, 2435–2447 (2009)

    Article  MATH  Google Scholar 

  52. Zhu, Y., Papademetris, X., Sinusas, A.J., Duncan, J.S.: A coupled deformable model for tracking myocardial borders from real-time echocardiography using an incompressibility constraint. Med. Image Anal. 14(3), 429–448 (2010)

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank Rabeh Djabri for English proofreading and Dr. Mathiron and Dr. Levy for their help in the clinical evaluation. Part of this work was funded by the Regional Council of Picardie and European Union/FEDER.

Author information

Authors and Affiliations

  1. Medical Computing Laboratory (LIMED), University of Abderrahmane Mira, 06000, Bejaïa, Algeria

    Ahror Belaid

  2. Mirada Medical Ltd, New Road, Oxford, OX1 1BY, UK

    Djamal Boukerroui

  3. Sorbonne universités, Université de Technologie de Compiègne, CNRS 7253 UMR/Heudiasyc, CS 60319, 60203, Compiègne Cedex, France

    Djamal Boukerroui

Authors
  1. Ahror Belaid
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Djamal Boukerroui
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahror Belaid.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Belaid, A., Boukerroui, D. Local maximum likelihood segmentation of echocardiographic images with Rayleigh distribution. SIViP 12, 1087–1096 (2018). https://doi.org/10.1007/s11760-018-1251-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11760-018-1251-7

Keywords

Search

Navigation