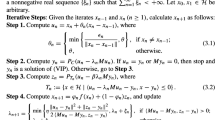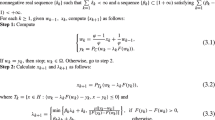Abstract
In this paper, we introduce two new iterative algorithms for solving monotone variational inequality problems in real Hilbert spaces, which are based on the inertial subgradient extragradient algorithm, the viscosity approximation method and the Mann type method, and prove some strong convergence theorems for the proposed algorithms under suitable conditions. The main results in this paper improve and extend some recent works given by some authors. Finally, the performances and comparisons with some existing methods are presented through several preliminary numerical experiments.












Similar content being viewed by others
References
Antipin, A.S.: On a method for convex programs using a symmetrical modification of the Lagrange function. Ekonomika i Mat. Metody 12, 1164–1173 (1976)
Cai, G., Gibali, A., Iyiola, O.S., Shehu, Y.: A new double-projection method for solving variational inequalities in Banach spaces. J. Optim. Theory Appl. (2018). https://doi.org/10.1007/s10957-018-1228-2
Chen, C., Ma, S., Yang, J.: A general inertial proximal point algorithm for mixed variational inequality problem. SIAM J. Optim. 25, 2120–2142 (2015)
Ceng, L.C., Hadjisavvas, N., Wong, N.C.: Strong convergence theorem by a hybrid extragradient-like approximation method for variational inequalities and fixed point problems. J. Glob. Optim. 46, 635–646 (2010)
Ceng, L.C., Anasri, Q.H., Yao, J.C.: Mann type iterative methods for finding a common solution of split feasibility and fixed point problems. Positivity 16, 471–495 (2012)
Censor, Y., Gibali, A., Reich, S.: The subgradient extragradient method for solving variational inequalities in Hilbert space. J. Optim. Theory Appl. 148, 318–335 (2011)
Censor, Y., Gibali, A., Reich, S.: Strong convergence of subgradient extragradient methods for the variational inequality problem in Hilbert space. Optim. Methods Softw. 26, 827–845 (2011)
Censor, Y., Gibali, A., Reich, S.: Algorithms for the split variational inequality problem. Numer. Algorithms 59, 301–323 (2012)
Censor, Y., Gibali, A., Reich, S.: Extensions of Korpelevich’s extragradientmethod for the variational inequality problem in Euclidean space. Optimization 61, 1119–1132 (2012)
Dang, Y., Gao, Y.: The strong convergence of a KM–CQ-like algorithm for a split feasibility problem. Inverse Probl. 27, 015007 (2011)
Dong, Q.L., Jiang, D., Gibali, A.: A modified subgradient extragradient method for solving the variational inequality problem. Numer. Algorithms (2018). https://doi.org/10.1007/s11075-017-0467-x
Facchinei, F., Pang, J.S.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer, Berlin (2003)
Fichera, G.: Sul problema elastostatico di Signorini con ambigue condizioni al contorno. Atti Accad. Naz. Lincei VIII. Ser. Rend. Cl. Sci. Fis. Mat. Nat. 34, 138–142 (1963)
Fichera, G.: Problemi elastostatici con vincoli unilaterali: il problema di Signorini con ambigue condizioni al contorno. Atti Accad. Naz. Lincei Mem. Cl. Sci. Fis. Mat. Nat. Sez. I VIII Ser. 7, 91–140 (1964)
Goebel, K., Reich, S.: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings. Marcel Dekker, New York and Basel (1984)
Harker, P.T., Pang, J.S.: A damped-Newton method for the linear complementarity problem. Lect. Appl. Math. 26, 265–284 (1990)
Hieu, D.V., Thong, D.V.: New extragradient-like algorithms for strongly pseu domonotone variational inequalities. J. Glob. Optim. 70, 385–399 (2018)
Kassay, G., Reich, S., Sabach, S.: Iterative methods for solving systems of variational inequalities in reflexive Banach spaces. SIAM J. Optim. 21, 1319–1344 (2011)
Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and Their Applications. Academic Press, New York (1980)
Konnov, I.V.: Combined Relaxation Methods for Variational Inequalities. Springer, Berlin (2000)
Konnov, I.V.: Equilibrium Models and Variational Inequalities. Elsevier, Amsterdam (2007)
Korpelevich, G.M.: The extragradient method for finding saddle points and other problems. Ekon. Mat. Metody 12, 747–756 (1976)
Kraikaew, R., Saejung, S.: Strong convergence of the Halpern subgradient extragradient method for solving variational inequalities in Hilbert spaces. J. Optim. Theory Appl. 163, 399–412 (2014)
Li, W., Xiao, Y.B., Huang, N.J., Cho, Y.J.: A class of differential inverse quasi-variational inequalities in finite dimensional spaces. J. Nonlinear Sci. Appl. 10, 4532–4543 (2017)
Liu, L.S.: Ishikawa and Mann iteration process with errors for nonlinear strongly accretive mappings in Banach spaces. J. Math. Anal. Appl. 194, 114–125 (1995)
Maingé, P.E., Gobinddass, M.L.: Convergence of one step projected gradient methods for variational inequalities. J. Optim. Theory Appl. 171, 146–168 (2016)
Maingé, P.E.: Regularized and inertial algorithms for common fixed points of nonlinear operators. J. Math. Anal. Appl. 34, 876–887 (2008)
Maingé, P.E.: A hybrid extragradient-viscosity method for monotone operators and fixed point problems. SIAM J. Control Optim. 47, 1499–1515 (2008)
Maingé, P.E.: Inertial iterative process for fixed points of certain quasinonexpansivemappings. Set Valued Anal. 15, 67–79 (2007)
Malitsky, Y.V., Semenov, V.V.: A hybrid method without extrapolation step for solving variational inequality problems. J. Glob. Optim. 61, 193–202 (2015)
Malitsky, Y.V.: Projected reflected gradient methods for monotone variational inequalities. SIAM J. Optim. 25, 502–520 (2015)
Mann, W.R.: Mean value methods in iteration. Proc. Am. Math. Soc. 4, 506–510 (1953)
Moudafi, A.: Viscosity approximationsmethods for fixed point problems. J. Math. Anal. Appl. 241, 46–55 (2000)
Polyak, B.T.: Some methods of speeding up the convergence of iterarive methods. Zh. Vychisl. Mat. Mat. Fiz. 4, 1–17 (1964)
Reich, S.: Constructive Techniques for Accretive and Monotone Operators. Applied Nonlinear Analysis, pp. 335–345. Academic Press, New York (1979)
Solodov, M.V., Svaiter, B.F.: A new projection method for variational inequality problems. SIAM J. Control Optim. 37, 765–776 (1999)
Stampacchia, G.: Formes bilineaires coercitives sur les ensembles convexes. C. R. Acad. Sci. 258, 4413–4416 (1964)
Suantai, S., Pholasa, N., Cholamjiak, P.: The modified inertial relaxed CQ algorithm for solving the split feasibility problems. J. Ind. Manag. Optim. (2018). https://doi.org/10.3934/jimo.2018023
Tinti, F.: Numerical solution for pseudomonotone variational inequality problems by extragradient methods. In: Giannessi, F., Maugeri, A. (eds.) Variational Analysis and Applications, vol. 79, pp. 1101–1128. Springer, Boston, MA (2005)
Thong, D.V., Hieu, D.V.: Modified subgradient extragradient method for inequality variational problems. Numer. Algorithms (2017). https://doi.org/10.1007/s11075-017-260-0452-4
Thong, D.V., Hieu, D.V.: Weak and strong convergence theorems for variational inequality problems. Numer. Algorithms (2017). https://doi.org/10.1007/s11075-017-0412-z
Thong, D.V., Hieu, D.V.: Modified subgradient extragradient algorithms for variational inequality problems and fixed point problems. Optimization 67, 83–102 (2018)
Thong, D.V., Hieu, D.V.: An inertial method for solving split common fixed point problems. J. Fixed Point Theory Appl. 19, 3029–3051 (2017)
Thong, D.V., Hieu, D.V.: Some extragradient-viscosity algorithms for solving variational inequality problems and fixed point problems. Numer. Algorithms. (2018). https://doi.org/10.1007/s11075-018-0626-8
Thong, D.V., Hieu, D.V.: New extragradient methods for solving variational inequality problems and fixed point problems. J. Fixed Point Theory Appl. 20, 129 (2018). https://doi.org/10.1007/s11784-018-0610-x
Thong, D.V., Hieu, D.V.: Modified Tseng’s extragradient algorithms for variational inequality problems. J. Fixed Point Theory Appl. 20, 152 (2018). https://doi.org/10.1007/s11784-018-0634-2
Thong, D.V., Gibali, A.: Two strong convergence subgradient extragradient methods for solving variational inequalities in Hilbert spaces. Jpn. J. Indust. Appl. Math. (2018). https://doi.org/10.1007/s13160-018-00341-3
Thong, D.V., Gibali, A.: Extragradient methods for solving non-Lipschitzian pseudo-monotone variational inequalities. J. Fixed Point Theory Appl. (2018). https://doi.org/10.1007/s11784-018-0656-9
Wang, Y.M., Xiao, Y.B., Wang, X., Cho, Y.J.: Equivalence of well-posedness between systems of hemivariational inequalities and inclusion problems. J. Nonlinear Sci. Appl. 9, 1178–1192 (2016)
Xu, H.K.: Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 66, 240–256 (2002)
Acknowledgements
The second named author is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant No. 101.01-2017.08.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Professor Pham Ky Anh on the Occasion of his 70th Birthday.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Thong, D.V., Vinh, N.T. & Cho, Y.J. Accelerated Subgradient Extragradient Methods for Variational Inequality Problems. J Sci Comput 80, 1438–1462 (2019). https://doi.org/10.1007/s10915-019-00984-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-019-00984-5
Keywords
- Variational inequality problem
- Extragradient method
- Subgradient extragradient method
- Inertial method
- Mann type method
- Viscosity method