1 Introduction

Worldwide glacier retreat is one of the most obvious and impressive manifestations of climate change (e.g., Mernild et al. 2013; Leclerq et al. 2014; Zemp et al. 2015). A detailed climatic interpretation of long-term glacier length records, taking into account differences in response times and climate sensitivity of individual glaciers, has revealed that glacier retreat can be fully explained by the rise in atmospheric temperature over the past 100 to 150 years (Leclercq and Oerlemans 2011). Due to the delay in glacier response, further retreat is inevitable, even if global warming would stop and the climate system would stabilize at the present state. On a worldwide scale, the impact of changes in glacier extent and volume is mainly through its effect on sea level. On a regional and local scale, glaciers fluctuations may affect meltwater supply (reservoirs, irrigation), security of infrastructure and buildings (ice avalanches, outbursts of glacial lakes), and tourist industry (ski areas, attractiveness of alpine scenery).

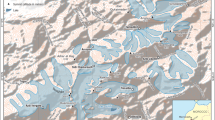
In this contribution, we report on a study of the Morteratsch Glacier (Vadret da Morteratsch, VdM in the following). This glacier is located in the southeastern part of Switzerland (Upper Engadin), is currently about 6 km long, and spans an altitudinal range of about 2200 to 4000 m (Fig. 1). The strong retreat of the VdM, especially during the past few decades, has resulted in a loss of attractiveness of the landscape in a region that lives almost entirely on tourism. The gravel road, starting at the railway station Morteratsch and gently rising from an altitude of 1896 to 2100 m over a distance of 3 km, is one of the most visited tourist tracks in Switzerland all year round. Unfortunately, during the past decade, the recession of the glacier has been so strong that the glacier front has retreated over a rock outcrop and becomes barely visible from the road. Further retreat will reduce the attractiveness of the Morteratsch valley in a significant way, because it will become increasingly difficult to access the glacier snout. The Community of Pontresina, in which the VdM is located, has therefore commissioned a preparatory study to find out if it is possible to slow down the retreat of the VdM. The idea for such a study was partly inspired by the apparent success of covering the small Diavolezza glacier by fleece to maintain a great deal of the winter snowpack throughout the summer. This glacier is of importance because its presence actually prevents the upper part of a ski run to become too steep (for its location see the arrow in Fig. 2).

Fig. 1
figure 1

Vadret da Morteratsch, photographed from a glider on 29 June 2003, looking south. Front positions are indicated for several years. The 2035 front position has been calculated for a scenario in which climate does not change. The corresponding equilibrium positions are shown in black. Note the Sahara dust band in the upper ablation zone. The gravel road to the glacier snout can be seen as a thin line in the bottom of the valley (to the right of the glacial river). The blue arrow points to the location of a small moraine-dammed lake (not visible), which is fed by melt water from the Vadret da la Fortezza (VF). The Vadret Pers is the glacier on the left, which was connected to the Vadret da Morteratsch until a few years ago (on the photo it still is). The position of the automatic weather station (AWS) is indicated by the small square

Full size image
Fig. 2
figure 2

Topographic map of the Vadret da Morteratsch/Vadret Pers glacier system.The railway station Morteratsch is close to the Little Ice Age (~ 1850) terminal moraine (at the right). The Diavolezza glacieret is indicated by an arrow. The upper station of the cable car is at D. The red (Vadret da Morteratsch) and purple (Vadret Pers) dots are spaced at 1 km distances along the flowlines as defined for the dynamical glacier model. The supply of ice mass from the Vadret Pers into the Vadret da Morteratsch, at km 5, has currently stopped. Courtesy of Bundesamt für Landestopografie, Köniz, Schweiz (2006)

Full size image

The scale of the VdM is much larger than the Diavolezza glacier, and the option of a fleece cover is not realistic. On a larger scale, mass can be added to a glacier by freezing of water at its surface, or by deposition of artificial snow. Snow has the additional advantage that it increases the albedo and thus reduces the amount of energy available at the surface for melting. This was clearly demonstrated by a “natural experiment” on 10–11 July 2000, when a large amount of snow was deposited on the VdM due to the passing of a cold front from the northwest and successive prolonged shower activity. During the event, two weather stations were operational in the ablation zone, which provided a unique opportunity to analyze the impact of summer snow on the surface mass balance of a glacier. The snow height in the lower ablation zone was about 20 cm (at 2100 m), increasing to 40 cm higher up (at 2640 m). The snowpack protected the underlying ice from melting. The effect of the snowfall event was analyzed with a calibrated energy balance model for the entire glacier with 20 m spatial resolution (Oerlemans and Klok 2004). The total amount of snow deposited on the glacier was estimated to be 224 mm w.e., whereas the calculated effect on the net mass balance turned out to be 354 mm w.e. The effect of this single summer snow event is equivalent to the effect of a 0.5 K lower summer temperature.

Inspired by the apparent effect of summer snow, we have investigated the possibility of making the mass budget of the VdM positive, or at least less negative, by artificially producing summer snow (“meltwater recycling”). Producing snow from meltwater is a trade-off between the availability of meltwater (summer half-year) and the presence of sufficiently cold conditions (winter half-year). The choice of the altitude zone is also crucial. On the lowest part of the glacier, temperatures are too high, which implies that the upper ablation zone is probably the best location to cover the melting ice surface by snow (the gently sloping part between km 3 and 4, marked in Fig. 2 by the blue area). Constructing reservoirs is considered to be undesirable and too costly. Fortunately, there is a moraine-dammed lake at the eastern side of the VdM (Fig. 1), which collects meltwater from a smaller glacier (Vadret da la Fortezza) and could be used as a source of water. In the basin of the Vadret Pers, there are several other small lakes which could eventually be used as well.

In section 2, we will investigate to what extent the meteorological conditions on the VdM allow for the production of summer snow in useful amounts. The basic idea is that the snow is used to cover an area as large as possible, in such a way that the ice never surfaces. In fact, this implies an optimization process which we have investigated.

In section 3, an ice-flow model is introduced and carefully calibrated by using the historical length data that go back to 1860. The model is a one-dimensional version of a code based on the Shallow Ice Approximation, with a parameterization of the three-dimensional geometry. The model is computationally fast, which is desirable because calibration against the past glacier length record requires many runs (> 100) to be carried out.

In section 4, we study the impact of mass balance perturbations generated by the surface snow on the future evolution of the VdM. Different climatic scenarios are considered, in which climate change is imposed as a steady rise in the equilibrium line altitude.

In section 5, we formulate our findings and make a statement about the usefulness and feasibility of a long-term artificial snow project on the VdM.

2 Meteorological conditions and production of snow

The long meteorological record from an AWS (Automatic Weather Station) located in the ablation zone of the VdM (Fig. 1) provides a solid basis to investigate the possibility of producing summer snow in sufficient amounts. The AWS has been installed in September 1995 on the glacier surface in the lower ablation area, and has been operated ever since (e.g., Oerlemans and Klok 2002; Oerlemans et al. 2009). In the course of time sensors have been improved and modified, and the station has been moved several times due to the glacier’s changing geometry. In the present analysis, we have used data for the period 2008–2011. Shortly before this period (in August 2007), the AWS was moved to a higher location (2250 m, see Fig. 1), and sensors were replaced or re-calibrated. These 4 years therefore provided an optimal set of homogeneous measurements.

Measured meteorological parameters are temperature, humidity, wind speed and direction, atmospheric pressure, incoming and reflected solar radiation, incoming and emitted terrestrial radiation, ice melt, and snow depth. All these parameters have been stored as 30-min average values. The region to which the calculation refers (Fig. 2, km 3–4) is at a 200-m higher altitude, and therefore temperature was adjusted with a standard lapse rate. Relative humidity was not changed, implying that the absolute humidities were also different. With the meteorological data as input, the amount of energy available at the surface for the melt process can be calculated.

The meteorological conditions for which snow can be produced depend on the type of snow lance used. Wet bulb temperature and wind speed are the most decisive factors. All the calculations were done for the Nessy Zero snow lance of the company Bächler Top Track AG (Ennetbürgen, Switzerland). This is an efficient system, but it requires water at high pressure with a sufficiently low (< 2 °C) temperature. The snow lance blows small droplets with an ice nucleus into the air. Due to the freezing of the droplets, the air is heated, and therefore a wind speed of at least 0.5 m/s is required to evacuate the heated air. Once snow has been deposited, it may start to melt, depending on the energy budget of the surface. A computer code was written to model the whole process (dynamics of the snowpack), yielding a cumulative snow mass curve showing how the situation evolves during the summer half-year. The model also calculates the volume of the lake (the possible water source), dealing with the variable input of meltwater from the Vadret da la Fortezza. Test runs were carried out for 1, 50, and 75 snow lances working simultaneously. It turned out that for more than 75 snow lances, the water source becomes a limiting factor in the spring and autumn months, when the input of meltwater to the lake is small. The simulations described in section 4 (the effect of artificial summer snow on future glacier length) show that for a lasting effect the amount of snow lances has to be larger.

The percentage of time during which snow can be produced is summarized in Table 1. We found that during the high summer months (July, August), snow can be produced only during 2 to 3% of the time. It is therefore important to start with the snow production as early as possible.

Table 1 Percentage (%) of the time during which snow can be produced with the NESSY snow lance, as calculated from the weather station data (temperature, humidity, wind)
Full size table

An example of a simulation with the snow production model is given in Fig. 3. The artificial snow mass is shown together with the wet bulb temperature, because this is the most important parameter that determines whether snow production is possible or not. During high summer, there were three short periods with sufficiently low temperatures to enable snow production. With the model, the effect of different parameters (wind speed, snow albedo, air temperature, humidity, area over which the snow from one lance is distributed, etc.) has been studied in detail (Haag 2016). To counter the high water demand in May and June, the production of snow could be started earlier.

Fig. 3
figure 3

An example of the evolution of an artificially produced snow cover in summer as simulated with the snow model

Full size image

The basic conclusion of the simulation is that it is possible to maintain a snow cover in the ablation zone of the VdM (at 2450 m) through the summer when sufficient water is available. For a larger area to be covered (0.5 to 0.8 km2), the lake mentioned above is not sufficient. So, a way has to be found to use the meltwater produced in the previous summer. This would have the advantage that snow can already be produced in winter, and it is more likely that a snow cover can be maintained also in a warmer climate.

The presence of a snow cover through the summer implies that ice melt at the surface will be prevented. During a typical summer at an altitude of 2450 m, an ice layer 3 to 4 m is melted and the water runs off. Therefore, the effect of a snow cover implies a significant positive effect on the surface mass balance. In the calculations with the glacier model discussed later, the specific mass balance b at the surface is a linear function of altitude z with an upper limit b max:

$$ b(z)=\beta \left(z\hbox{-} ELA\right) $$
(1)
$$ \mathrm{if}\ b(z)>{b}_{\mathrm{max}}=>b(z)={b}_{\mathrm{max}} $$
(2)

Here, ELA is the equilibrium-line altitude and β the balance gradient.

Several modeling studies of the mass balance distribution on the Morteratsch glacier system have been carried out (Oerlemans and Klok 2004; Nemec et al. 2009; Van Pelt 2010), and these studies suggest that a value of 0.0065 m w.e. m−1 for β can be taken as a characteristic value. However, the value of the specific balance in the upper part of the glacier is subject to large uncertainties, because little is known about the precipitation gradients at the higher elevations. In this study, we use a value of 3.0 m w.e. a−1. This seems to be a bit on the high side, but we believe that in earlier studies the effect of a very strong north-south gradient in precipitation across the Bernina mountain has not been taken into account sufficiently. We also note that an ice core, taken in the highest part of the accumulation basin (at 3850 m a.s.l.), yielded an accumulation rate for the period 1992–2001 of 2.6 ± 0.8 m w.e. a−1 (Sodemann et al. 2006).

The resulting specific balance along the flowline of the VdM is shown in Fig. 4. Because the specific balance depends linearly on altitude, the specific balance curve also reflects the altitudinal profile, except for the upper part. Keeping the surface in part of the ablation zone covered by artificial snow throughout the summer implies that the specific balance becomes effectively zero. When this would be done for the glacier surface between km 3 and km 3.5 (Fig. 2), the resulting surface balance perturbation would look like the dashed curve in Fig. 4. This balance profile will serve as input for our standard meltwater-recycling experiment. Because the zone of the mass balance perturbation is several kilometers upstream from the glacier snout, it has to be expected that the response of the front position will not be immediate but will take time. Results from the flowline model will shed more light on this.

Fig. 4
figure 4

Specific balance along the Morteratsch flowline for the year 2015. The dashed line shows the perturbation resulting from maintaining a snow cover at the surface between 3.0 and 3.5 km (specific balance = 0)

Full size image

3 Ice-flow model

Projection of the future behavior of a particular glacier requires careful calibration against observed changes in the past. Because a larger valley glacier has a response time of decades, such a calibration is a meaningful approach to test a model and to define an appropriate initial state for integration in time. The procedure of “dynamic calibration”, in which a mass balance history is constructed in such a way that observed and simulated glacier length records match, was first applied to Nigardsbreen (Oerlemans 1997). Since the method is essentially an iterative optimization procedure, many model runs (typically 100) are required, which puts some constraints on the glacier flow model.

A flowline model, based on the Shallow Ice Approximation (SIA; e.g. Van der Veen 2013), was considered to be the most appropriate tool. Ice thickness and velocity are calculated along a central flowline, and the three-dimensional geometry is parameterized by use of a trapezoidal cross-section, with parameters that vary with distance along the flowline. The use of a trapezoidal cross-section implies that the glacier width depends on the ice thickness, depending on the slope of the valley walls.

Two flowlines are actually used: one for the VdM and one for the Vadret Pers (Fig. 2). The length of the Vadret Pers is restricted to 4.4 km, because at that length it delivers its mass to the VdM. This is easily accommodated in the model. The Vadret Pers decoupled from the VdM just recently, and this provides an important constraint for model calibration. Although not the target of this study, the future evolution of the Vadret Pers is also calculated.

The SIA model with trapezoidal cross-section has been used in many studies, so we do not describe the mathematical derivation of the relevant equations and method of numerical solution (see e.g., Oerlemans 1997). In the SIA model, longitudinal stress gradients are neglected and there is always a balance between the driving stress, which is proportional to the local ice thickness and the surface slope, and the basal shear stress (friction). A distinction is made between internal deformation and sliding. A Weertman-type sliding law is used, implying that sliding dominates over deformation for smaller ice thickness (e.g., Van der Veen 2013). The spatial resolution along the flowlines is 20 m. The parameterization of the bed topography is based on the work of Zekollari et al. (2013). The parameters of the trapezoidal cross-sections for the flowline model used here were estimated from their map of bedrock elevation. This map is based on a DEM for the ice free areas, and on ice thickness measurements for the flatter parts covered by glacier ice.

The calibration of the model is carried out by adjusting the equilibrium-line altitude every 5 years in such a way that the rms-difference between simulated and observed glacier length (taken from glaciological Reports 2016) is minimal. A few hundred runs had to be carried out to arrive at the best possible solution. The result is shown in Fig. 5. The observed length variations apparently imply that a significant rise of the equilibrium line took place during the periods 1900–1940 and 1965–2015, with a steep drop in between. According to the model simulation, a 200-m increase in the ELA since the Little Ice Age maximum stand is required to explain the observed retreat of the VdM, which is in broad agreement with earlier studies (e.g., Huss et al. 2010; Zekollari et al. 2014). The correlation between the observed and simulated length is very high (> 0.99), the standard deviation of the difference being 28 m. Note that, because of the glacier’s response time of several decades, it makes no sense to refine the temporal resolution of the ELA history. An alternative method is to use meteorological observations from a nearby climate station (Segl-Maria) to make a reconstruction of the equilibrium-line history. Such a reconstruction was published in Oerlemans (2012), but imposing it to the glacier model leads to a significantly less accurate simulation of the historic length variations. Since an accurate definition of the current state (and imbalance) is essential for an optimal projection of future evolution, preference was given to the equilibrium-line history as produced by the calibration method described above.

Fig. 5
figure 5

Calibrated simulation of glacier length (scale at right) for the Vadret da Morteratsch and Vadret Pers. The red dots show the observed glacier length. The corresponding reconstructed equilibrium-line history (E) is also shown (scale at left)

Full size image

After the calibration period (1860–2015), the model has been integrated further in time with an ELA equal to its mean value over the period 2001–2015 (2982 m). This was done to find out to what length the glacier would evolve if the climate were to remain “constant”, and it also provides an idea of the imbalance of the current state. Admittedly, the choice of the period 2001–2015 is ambiguous. It is a compromise between including the recent warming on one hand, and not putting too much weight to individual years on the other hand. Apparently, in the long run the glacier will stabilize for a length of 4.7 km, which is actually on the bump in the bedrock (located between x = 4.3 and x = 4.9 km). In 2040, the VdM is already rather close to this (theoretical) equilibrium state (length 4.85 km). It should be noted that these findings are in good agreement with the three-dimensional model simulation of Zekollari et al. (2014).

In the length curve in Fig. 5, two kinks can be seen at the years 2017 and 2035. These mark the years at which the glacier front passes a step in the bedrock. Because the model has a small gridpoint distance (20 m), the steps are well resolved. This is further illustrated in Fig. 6. Note that in the year 2015 the glacier front has retreated on the bump in the bedrock at x = 5.5 km, but some stagnant ice has remained at the foot of the step (arrow in the figure), which has also been observed in reality. Apparently, the model is able to resolve features that are a direct consequence of the complex terrain.

Fig. 6
figure 6

Surface elevation at different times for the Vadret da Morteratsch flowline. The curve for 2040 has been calculated for a scenario in which the climate does not change

Full size image

4 The effect of artificial snow on future glacier length

The model simulation discussed in section 3 serves as a reference numerical experiment for assessing the effect of artificial mass balance perturbations. Calculations were performed for different scenarios of climate change, namely, (i) ELA equal to the 2001–2015 mean value (+ ELAref); (ii) ELA = ELAref plus a 1 m per year increase; (iii) ELA = ELAref plus a 2 m per year increase; (iv) ELA = ELAref plus a 4 m per year increase. Energy balance modeling has revealed that for glaciers in the Alps, a 100 m increase in the ELA corresponds to an annual mean temperature increase between 0.8 and 1.2 K, or, alternatively, a precipitation decrease of 25 to 35% (Oerlemans 2001).

Scenario (iii) can be considered as an optimistic one (the Paris agreement becoming reality), corresponding to an increase in temperature of 0.022 K a−1 and in precipitation of 0.08% a−1. Note that the imposed rise in ELA from 2015 onwards is on top of the 2001–2015 mean value, which is higher than the “climatological mean” of the period 1985–2015.

Scenario (iv) is a more pessimistic one. It would correspond to a further temperature rise of about 3.5 K in the next 80 years, likely to occur when carbon dioxide emissions remain at the present level (IPCC 2014). With such a temperature rise the production of artificial snow would in fact also become impossible within a few decades. The modeling results for scenario (iv) show some other peculiar features (the glacier splits in two parts) and are therefore discussed separately in section 5.

Generally speaking, uncertainties in the projected changes for the Alps are large. Recent warming in central Europe has been substantially larger than the global, or even European, mean, and this may be partly related to internal variability of the ocean-atmosphere system that is not a direct consequence of global greenhouse warming. It therefore remains unclear whether the enhanced warming (as compared to the global mean) will persist in the coming decades.

The solid lines in Fig. 7 show the evolution of the glacier length for scenarios (i), (ii), and (iii). For scenario (iii), the retreat is dramatic and accelerates during the last 20 years of the twenty-first century. According to the bed profile shown in Fig. 6, a lake will form when the glacier length becomes less than 4.4 km. This would imply that from 2075 onwards the glacier would have a calving front, probably enhancing the retreat. The formation of lakes in landscapes with retreating glaciers is expected to be widespread (Haeberli et al. 2016). Such lakes can be attractive but also dangerous. A large lake at the foot of over-steepened slopes with hanging glaciers producing ice avalanches implies the risk of flood waves.

Fig. 7
figure 7

Overview of climate change experiments with (dashed lines) and without (solid lines) artificial snow. The numbers +1 and +2 m/yr refer to the imposed rise of the equilibrium line

Full size image

Studies of lacustrine glacier calving rates have been carried out and the major processes have been identified (e.g., Funk and Röthlisberger 1989; Naruse and Skvarca 2000; Benn et al. 2007). However, in view of the large uncertainty in the potential lake geometry, at this stage we have not attempted to model the effect of calving.

The dotted curves in Fig. 7 show what would happen if part of the glacier is covered continuously by snow during the summer from 2017 onwards. The deposition of snow is between x = 3 and 4 km, covering an area of about 0.8 km2. The first conclusion to be drawn is that it takes about 10 years before the mass balance signal has an effect on the position of the glacier front. From 2028, the front position stabilizes and a slow advance follows. In the case of no climate change, the equilibrium glacier length, approached around 2080, is 5.7 km. This is close to the present-day glacier length. In the case scenario (iii), the artificial snow stabilizes the glacier front until about 2050, and then retreat sets in again. In 2100, the glacier length would then be equal to the length for the case without climate change and without artificial snow.

The difference in glacier length for the no-snow and snow cases is typically 0.8 km in 2100. We therefore conclude that an artificial snow cover over an area of 0.8 km2 in the ablation zone of the VdM has a significant effect on the long-term glacier length. Longitudinal profiles for the year 2100 are shown in Fig. 8. Only for the scenario with no climate change and artificial snow the VdM evolves in such a way that the front position is just below the rock step that has recently become free of ice. In fact, this once more illustrates how far the actual glacier shape is out of balance with the present-day climatic conditions.

Fig. 8
figure 8

Longitudinal profiles of the VdM in the year 2100 as calculated for the various scenarios

Full size image

5 A more extreme scenario

As noted in section 4, climate change scenario (iv) has a more dramatic impact on the future evolution of the VdM. The results for this scenario are shown in the form of longitudinal profiles in Fig. 9. As expected, scenario (iv) leads to a further strong retreat of the VdM. In the year 2050, the glacier front would be on the bedrock bump around x = 4.6 km, and at the verge of entering a phase of vary rapid retreat through a newly formed lake in the overdeepening. The model predicts that in the year 2090, the glacier front will be on the steep slope (arrow at x = 2.5 km) and the whole flatter part of the glacier will be gone. Once the glacier front is in the overdeepening, the retreat is virtually unstoppable due to the altitude mass balance feedback (lower surface -> more ablation). The effect of calving, not taken into account in our model simulation, would make the retreat even faster. A long-lasting drop in the equilibrium line of more than 300 m would be needed to make the glacier grow again.

Fig. 9
figure 9

Longitudinal profiles of the VdM as calculated for scenario (iv), for the case without artificial snow (a) and with artificial snow (b). The blue dashed lines indicate the level of potential lakes. The glacier front position in the year 2090 is indicated with a small arrow

Full size image

In Fig. 9, the same set of snapshots is shown, now for the case with artificial snow. Overall, the rate of retreat would be halved, and in the year 2070 the glacier front is still on the bedrock bump and the glacier lake would not be formed. In fact, the glacier splits into two parts. In the year 2090, there would be an upper glacier having the front position at the same location as in the case without artificial snow (arrow). Then there is a decoupled lower glacier, fed by the addition of artificial snow and having the ablation zone at 4 > × > 4.5 km. This glacier will persist as long as the mass balance between at 3 > × > 4 km is kept to zero. It is clear that this would be an impossible task to achieve with summer snow, because meanwhile summer temperatures would be so much higher. However, more meltwater would be available in late spring and fall from the upper glacier, and this could be used to produce snow outside the summer months.

6 Conclusion

Based on a modeling approach, we have investigated the potential effect of deposition of artificial snow on the future evolution of the VdM. Models require careful calibration, and we believe existing datasets have allowed us to do so. The detailed meteorological observations in the ablation zone of the VdM have been a good starting point to evaluate the possibility of maintaining a snow cover through the summer. The long record of glacier length observations, on the other hand, has allowed us to carry out fine tuning of the glacier flow model. We therefore think that our study is more than a qualitative statement that artificial snow may help to reduce glacier retreat. The unique data available for the VdM just mentioned, including the ice thickness measurements carried out by Zekollari et al. (2013), have made it possible to quantify the process of snow deposition, reduced ice melt, and dynamic glacier response.

The main conclusion of our study is that deposition of artificial snow on the VdM can have a significant effect of future evolution of the VdM. It takes about 10 years before the snow deposition starts to work out on the position of the glacier snout. Then the snow deposition appears to become effective, because it basically prevents the glacier front to retreat rapidly on the steep slope of the large bump in the bed just upstream of km 5. The difference in glacier length between the snow and no-snow experiments then becomes 400 to 500 m within a decade.

Like many large valley glaciers, the VdM has a bed profile with a pronounced overdeepening where a lake is expected to form (Lej da Morteratsch). A larger lake immediately at the foot of high steep slopes with unsupported hanging glaciers and degrading permafrost has the potential to create strongly increased risks from impact/flood waves. This would not only concern the access to the glacier but even the railway at Morteratsch and infrastructure further down valley. Our results have shown that the deposition of artificial summer snow can shift the formation of such a lake forward in time by decades. In combination with even modest mitigation of climate change in the near future, artificial snow could make the difference between a valley with a large lake, or a valley with a glacier in the second half of this century.

We believe that the major uncertainty of projections of glacier length comes from the wide range of climate change scenarios. The choice of reference period is also affecting the results. For instance, if the reference period 1986–2015 would be taken instead of 2001–2015, after a few decades the projected glacier length would be 300 m larger for most scenarios.

Here we do not formulate an opinion on implementation of an artificial snow project on the VdM, but merely provide information on the feasibility. Keeping an area of 0.8 km2 covered by snow for many decades is an enormous and expensive task, but it may be technically possible. There are of course many environmental and political aspects that require careful evaluation.