Abstract
Considerable variability exists in simulations of the future climate. This variability is caused by differences in the parameterisations across general circulation models (GCMs), the initial conditions used and the different assumptions made as to how emissions will evolve in the future. As a result, there is considerable disagreement between available projections of climate variables, which can be used to quantify the uncertainty each variable exhibits. This leads to the question—which variables (or set of variables) are more reliable for use in climate change impact assessments. This research presents a framework to quantify the relative reliability amongst a range of upper air atmospheric variables. This is made possible by pooling simulations across multiple models, trajectories (scenarios) and initial conditions in a rank-transformed space. A metric named the variable reliability score (VRS) assesses the relative reliabilities across different atmospheric variables on a common scale. The VRS has been applied to calculate the total reliability as well as reliability from each source of uncertainty, namely model, scenarios and initial conditions. This comparison helps to decide if more models, scenarios or ensembles are required for uncertainty analysis of climate change impact assessment.
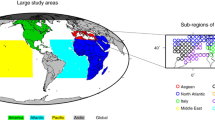
The variables compared include geopotential height and its north-south difference, specific humidity, eastward wind and northward wind, all at the 500 and 850 hPa pressure levels. These variables were chosen based on availability of data and their documented use in previous climate change impact assessment studies worldwide. A regional assessment of VRS over 21 regions around the world shows that though the magnitude of VRS varies spatially, the ranked reliability of the variable rank remains relatively similar. On average, the lowest reliability is associated with geopotential height, whilst wind speeds and the north-south difference of geopotential height have higher reliability.




Similar content being viewed by others
References
Abatzoglou JT, Brown TJ (2012) A comparison of statistical downscaling methods suited for wildfire applications. Int J Climatol 32:772–780. https://doi.org/10.1002/joc.2312
Cavazos T, Hewitson BC (2005) Performance of NCEP-NCAR reanalysis variables in statistical downscaling of daily precipitation. Clim Res 28:13
Chen J, Brissette FP, Leconte R (2011) Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J Hydrol 401:190–202. https://doi.org/10.1016/j.jhydrol.2011.02.020
Eghdamirad S, Johnson F, Woldemeskel F, Sharma A (2016) Quantifying the sources of uncertainty in upper air climate variables. J Geophys Res Atmos 121:3859–3874. https://doi.org/10.1002/2015JD024341
Eghdamirad S, Johnson F, Sharma A (2017) Using second-order approximation to incorporate GCM uncertainty in climate change impact assessments. Clim Chang 142:37–52
Fowler HJ, Blenkinsop S, Tebaldi C (2007) Linking climate change modelling to impacts studies: recent advances in downscaling techniques for hydrological modelling. Int J Climatol 27:1547–1578. https://doi.org/10.1002/joc.1556
Fowler KJA, Peel MC, Western AW, Zhang L, Peterson TJ (2016) Simulating runoff under changing climatic conditions: revisiting an apparent deficiency of conceptual rainfall-runoff models. Water Resour Res 52:1820–1846. https://doi.org/10.1002/2015wr018068
Giorgi F, Francisco R (2000) Uncertainties in regional climate change prediction: a regional analysis of ensemble simulations with the HADCM2 coupled AOGCM. Clim Dyn 16:169–182
Gleckler PJ, Taylor KE, Doutriaux C (2008) Performance metrics for climate models. J Geophys Res 113:D06104. https://doi.org/10.1029/2007JD008972
Hawkins E, Sutton R (2009) The potential to narrow uncertainty in regional climate predictions. Bull Am Meteorol Soc 90:1095–1107. https://doi.org/10.1175/2009bams2607.1
Hawkins E, Sutton R (2011) The potential to narrow uncertainty in projections of regional precipitation change. Clim Dyn 37:407–418
Huth R (1999) Statistical downscaling in central Europe: evaluation of methods and potential predictors. Clim Res 13:91–101
IPCC (2013) Climate Change 2013: The Physical Science Basis. Contribution of working group I to the fifth assessment report of the Intergovernmental Panel on Climate Change. Cambridge, United Kingdom and New York, NY, USA
Johnson F, Sharma A (2009) Measurement of GCM skill in predicting variables relevant for hydroclimatological assessments. J Clim 22:4373–4382. https://doi.org/10.1175/2009jcli2681.1
Johnson F, Westra S, Sharma A, Pitman AJ (2011) An assessment of GCM skill in simulating persistence across multiple time scales. J Clim 24:3609–3623. https://doi.org/10.1175/2011jcli3732.1
Kalnay E et al (1996) The NCEP-NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77:35
Knutti R, Furrer R, Tebaldi C, Cermak J, Meehl GA (2010) Challenges in combining projections from multiple climate models. J Clim 23:2739–2758. https://doi.org/10.1175/2009jcli3361.1
Knutti R, Sedláček J, Sanderson BM, Lorenz R, Fischer EM, Eyring V (2017) A climate model projection weighting scheme accounting for performance and interdependence. Geophys Res Lett. https://doi.org/10.1002/2016gl072012
Koster RD et al (2006) GLACE: the global land-atmosphere coupling experiment. Part I: Overview. J Hydromet 7:590–610
Mehrotra R, Sharma A (2006) A nonparametric stochastic downscaling framework for daily rainfall at multiple locations. J Geophys Res 111:D15101. https://doi.org/10.1029/2005JD006637
Mehrotra R, Sharma A (2015) Correcting for systematic biases in multiple raw GCM variables across a range of timescales. J Hydrol 520:214–223. https://doi.org/10.1016/j.jhydrol.2014.11.037
Mehrotra R, Evans JP, Sharma A, Sivakumar B (2014a) Evaluation of downscaled daily rainfall hindcasts over Sydney, Australia using statistical and dynamical downscaling approaches. Hydrol Res 45:226. https://doi.org/10.2166/nh.2013.094
Mehrotra R, Sharma A, Bari M, Tuteja N, Amirthanathan G (2014b) An assessment of CMIP5 multi-model decadal hindcasts over Australia from a hydrological viewpoint. J Hydrol 519:2932–2951. https://doi.org/10.1016/j.jhydrol.2014.07.053
Najafi MR, Moradkhani H, Wherry SA (2011) Statistical downscaling of precipitation using machine learning with optimal predictor selection. J Hydrol Eng 16:650–664. https://doi.org/10.1061/(asce)he.1943-5584.0000355
Pierce DW, Barnett TP, Santer BD, Gleckler PJ (2009) Selecting global climate models for regional climate change studies. Proc Natl Acad Sci U S A 106:8441–8446. https://doi.org/10.1073/pnas.0900094106
Pui A, Sharma A, Santoso A, Westra S (2012) Impact of the El Nino-southern oscillation, Indian Ocean dipole, and southern annular mode on daily to subdaily rainfall characteristics in East Australia. Mon Weather Rev 140:1665–1682
Raju KS, Nagesh Kumar D (2014) Ranking of global climate models for India using multicriterion analysis. Clim Res 60:103–117. https://doi.org/10.3354/cr01222
Sachindra DA, Huang F, Barton A, Perera BJC (2014a) Statistical downscaling of general circulation model outputs to precipitation-part 1: calibration and validation. Int J Climatol: n/a-n/a https://doi.org/10.1002/joc.3914
Sachindra DA, Huang F, Barton A, Perera BJC (2014b) Statistical downscaling of general circulation model outputs to precipitation—part 1: calibration and validation. Int J Climatol 34:3264–3281. https://doi.org/10.1002/joc.3914
Sachindra DA, Huang F, Barton A, Perera BJC (2014c) Statistical downscaling of general circulation model outputs to precipitation—part 2: bias-correction and future projections. Int J Climatol 34:3282–3303. https://doi.org/10.1002/joc.3915
Tripathi S, Srinivas VV, Nanjundiah RS (2006) Downscaling of precipitation for climate change scenarios: a support vector machine approach. J Hydrol 330:621–640. https://doi.org/10.1016/j.jhydrol.2006.04.030
Van Vuuren DP et al (2011) The representative concentration pathways: an overview. Clim Chang 109:5–31
Woldemeskel FM, Sharma A, Sivakumar B, Mehrotra R (2012) An error estimation method for precipitation and temperature projections for future climates J Geophys Res Atmos 117:D22104. https://doi.org/10.1029/2012JD018062
Woldemeskel FM, Sharma A, Sivakumar B, Mehrotra R (2014) A framework to quantify GCM uncertainties for use in impact assessment studies. J Hydrol 519:1453–1465. https://doi.org/10.1016/j.jhydrol.2014.09.025
Woldemeskel F, Sharma A, Sivakumar B, Mehrotra R (2016) Quantification of precipitation and temperature uncertainties simulated by CMIP3 and CMIP5 models. J Geophys Res: Atmos 121:3–17
Xu C-y (1999) Climate change and hydrologic models: a review of existing gaps and recent research developments. Water Resour Manag 13:369–382. https://doi.org/10.1023/a:1008190900459
Yip S, Ferro CAT, Stephenson DB, Hawkins E (2011) A simple, coherent framework for partitioning uncertainty in climate predictions. J Clim 24:4634–4643. https://doi.org/10.1175/2011jcli4085.1
Acknowledgements
The Australian Research Council is acknowledged for financial support for this study. The World Climate Research Programme’s Working Group on Coupled Modelling, responsible for CMIP, is acknowledged for making model simulations in Table 1 available. NOAA/OAR/ESRL PSD is acknowledged for the NCEP reanalysis data used in this study.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Eghdamirad, S., Johnson, F. & Sharma, A. How reliable are GCM simulations for different atmospheric variables?. Climatic Change 145, 237–248 (2017). https://doi.org/10.1007/s10584-017-2086-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-017-2086-x