1 Introduction

Climate change, characterized by global warming and its effect on human society, affects the spatiotemporal characteristics of precipitation and increases the frequency of extreme events, such as floods and droughts (Vörösmarty et al. 2010). According to the fourth IPCC report (Du 2007), significant trends in temperature and precipitation were observed around the world, but with different magnitudes. The impacts of those trends in the mid-term are notable in several aspects. In particular, the stress on hydrology resources is expected to intensify. In this respect, several studies have been carried out to determine the impact on water resources (Arnell 1999; Middelkoop et al. 2001; Reilly et al. 2003; Christensen et al. 2006) and agriculture (Moynagh and Schimmel 1999; Li et al. 2015; Zhang et al. 2016). Precipitation changes, which include a greater number of extreme events and longer dry periods, together with temperature increases that increase evapotranspiration, will have negative impacts on agriculture. Particularly in Southern Europe, these trends could exacerbate the existing conditions in areas already vulnerable to climatic variability, reducing water availability. The Mediterranean area may be particularly sensitive. Some authors reported significant changes in precipitation patterns with decreasing precipitation trends for the Mediterranean (Alpert et al. 2002; Norrant and Douguédroit 2006) and significant changes in extreme events, with higher rainfall concentrations in a small number of events, and more frequent and extreme droughts (Easterling 2000; Burt et al. 2015).

The changing properties of precipitation extremes have received increasing public attention both in China and the rest of the world (Ge et al. 2016). Since the 2000s, China has experienced a high frequency of floods (Ren et al. 2000; Yan and Yang 2000; Lodh and Raghava 2014). For example, there was torrential rain in Beijing on 21 July 2012 and flooding in Nanjing on 2 June 2015. Li et al. (2015) indicated that in China, there is less co-occurrence of consecutive wet and dry days, and more joint extreme heavy precipitation events with meteorological, public safety, and economical implications, involving less risk of flood and drought co-occurrence in the same year, but higher risk of floods. Li et al. (2011) indicated that flood disasters have increased in response to the higher frequency of intense precipitation events and consequent amplification of their concentration indices and precipitation concentration. Zhang et al. (2015) showed that indices representing temporal variations of regional heavy precipitation display strong inter-decadal variability, with limited evidence of long-term trends. Such indicators vary markedly depending on precipitation type, season, and region. Analysis of precipitation extremes in Xinjiang, western China, also revealed increasing precipitation variability and high-intensity precipitation (Zhang et al. 2012). The overall amount of precipitation has barely changed, though its intensity and frequency has increased.

In this paper, the extreme precipitation in the northern region is used as a research example to show that risk analysis of extreme precipitation can improve the future diagnosis of flood risk, variability, and spatial pattern in Xinjiang, China. It is hoped that the results of this study can provide reference points for global climate change and provide some decision-making value for the prevention of disasters caused by extreme climate events.

2 Study area

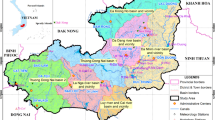
The northern Xinjiang area extends from 42° to 50° N, and 79° to 92° E (Fig. 1), enclosing an area of more than 398,456 km2, one twentieth of the total size of China. The northern region includes Changji and Boertala Prefectures, Urumchi, Kelamayi, Shihezi, and Kuitong Cities, and the Yili, Tacheng, and Aletai Regions. Situated deep in the interior of Asia and unaffected by oceanic air currents, the northern Xinjiang Uygur Autonomous Region experiences a typical continental climate, with highly fluctuating temperature, significant differences in diurnal temperature amplitude, abundant sunshine, intense evaporation, and little precipitation. The mean annual temperature of Xinjiang is 8 °C; the hottest month is July, averaging at about 25 °C, and the coldest is January, averaging at −20 °C in the north. The mean annual snow depth is 60 cm, reaching a maximum of 1–2 m in the mountainous areas.

Fig. 1
figure 1

Region of focus and observation stations. The map was generated using ArcGIS 10.2

Full size image

3 Data and methodology

3.1 Data sources

The data used in the study were daily precipitation series at 37 observatory stations in North Xinjiang, and were provided by the National Climatic Centre of China, China Meteorological Administration (shown in Fig. 1) for the period from 1 January 1961 to 31 December 2010. This institution performed quality control of the dataset prior to its release, and homogeneous detection for the dataset was also done (Li et al. 2011). In total, missing data accounts for 0.05% of the data series. The station data used in this study were screened for missing values, and only those stations with data records that were at least 95% complete for the period of 1961–2010 were included in our analysis. The missing data were interpolated using a simple linear correlation method between their neighboring stations. Finally, 37 stations, whose locations are shown in Fig. 1, were chosen for this study.

The climate stations report maximum daily precipitation based on annual maximum daily precipitation. To analyze the maximum daily precipitation through daily precipitation over the study period and area (Table 1), extreme value theory (EVT) was used. To reveal maximum daily precipitation, scatter diagrams were used as examples of the sites (Beitashan, Yining, Urumqi, and Habahe).

Table 1 Summary of annual maximum daily precipitation
Full size table

3.2 Data processing methodologies

In order to describe the behavior of extreme rainfall at a particular area (North Xinjiang), it is necessary to identify the distribution(s) that best fits the data. In this study, we use three parameter extreme value distributions (generalized extreme value, generalized Pareto), which are considered to be the best-fitting probability distribution function to extreme precipitation data. In probability theory and statistics, the generalized extreme value (GEV) distribution is a family of continuous probability distributions developed within extreme value theory to combine the Gumbel, Fréchet, and Weibull families, also known as type I, II, and III extreme value distributions (Hosking and Wallis 2005). In statistics, the generalized Pareto distribution (GPD), a family of continuous probability distributions, is often used to model the tails of other distributions (Hosking and Wallis 1987), shown in Table 2. Details on these distributions can be found in the works of Hosking and Wallis (2005) and Saghafian et al. (2014).

Table 2 List of distributions used in this study
Full size table

4 Results and discussion

4.1 GEV fitting

We used the established GEV extreme value model. The theory and approaches are applicable to distributions of extreme minima by analyzing the variable X (Bonacci 1991; Embrechts et al. 1997). The cumulative distribution function (CDF) of the GEV is given by

$$ F(x)= \exp \left\{-{\left(1+\kappa \frac{x-\zeta}{\beta}\right)}^{-\frac{1}{\kappa}}\right\}. $$
(1)

Here, \( 1+\frac{\kappa \left( x-\zeta \right)}{\beta}>0 \), and ς, β, and κ represent the position, scale, and shape parameters. If κ = 0, then

$$ F(x)= \exp \left\{- \exp \left(\frac{x-\varsigma}{\beta}\right)\right\}. $$
(2)

when κ = 0,κ > 0, and κ < 0, we have the CDF of the Gumbel, Frechet, and the negative CDF of the Weibull distributions. Thus, we have established the following extreme value model:

  1. 1.

    Model 1: ς, β, and κ are the constant values

  2. 2.

    Model 2: ς and β are the constant values; κ = 0

  3. 3.

    Model 3: ς = a + b ∗year, β represents the constant values; κ = 0

  4. 4.

    Model 4: ς = c + d ∗year, β represents the constant values; κ = 0

  5. 5.

    Model 5: ς is the constant value,β = exp(a + b ∗year), κ is the constant value

  6. 6.

    Model 6: ς is the constant value,β = exp(a + b ∗year), κ = 0

  7. 7.

    Model 7: ς = a + b ∗year, β = exp(c + d ∗year), κ is the constant value

  8. 8.

    Model 8: ς = a + b ∗year, β = exp(c + d ∗year), κ = 0

In this section, we analyze special case models 1 and 2. We used a likelihood ratio test, i.e., if L 1 and L 2are the maximum likelihood values for models 1 and 2, then λ =  − 2 log(L 2/L 1). We considered one degree of freedom of the chi-squared distribution for estimation purposes (degrees of freedom based on various adjustments of the parameters). In hypothesis testing problems, approximation of real-world data was used instead of infinity. Therefore, at a 5% significance level, the two-parameter model 2 (assumption\( -2 \log \left({L}_2/{L}_1\right)<{x}_{1,0.95}^2=3.84 \)) was preferred. In practice, because the annual maximum values were not completely independent, this description would be most effective.

Figure 2a–d shows that the annual maximum daily rainfall and time (years) have a certain line trend. We built models 3 and 4 to explain this problem, approaching three to four parameters. Similarly, we used a standard of likelihood ratio test to determine whether the trends described in models 3 and 4 were significant. Furthermore, we conducted a comparison of fitting results by means of a QQ plot and density map. There is a quantile forecasting QQ plot (Fig. 4) of the fitted model. For example, to test the fit of model 1, we depicted the sort value (in ascending order) of the annual maximum daily rainfall observed by the expected percentile y i , which was obtained by F(y i ) = (i − 0.375)/(n + 0.25) simulation, where F is in Eq. (1) of the accumulation function. Similarly, concerning the fit for model 2, we depicted the sort value following the same procedure described for model 1. The density function was graphed to compare models and non-parametric model fitting density.

Fig. 2
figure 2

Annual maximum daily precipitation recorded in a Beitashan, b Habahe, c Urmuqi, and d Yining from 1961 to 2010

Full size image

Among those, the models 1 and 2 fitting density computations are

$$ f(x)=\frac{1}{\widehat{\beta}}{\left(1+\widehat{\kappa}\frac{x-\widehat{\varsigma}}{\widehat{\beta}}\right)}^{-\frac{1}{\widehat{\kappa}+1}}\times \exp \left\{-{\left(1+\widehat{\kappa}\frac{x-\widehat{\varsigma}}{\widehat{\beta}}\right)}^{\frac{1}{\widehat{\kappa}}}\right\} $$

and

$$ f(x)=\frac{1}{\widehat{\beta}} \exp \left(-\frac{x-\widehat{\varsigma}}{\widehat{\beta}}\right)\times \exp \left\{- \exp \left(-\frac{x-\widehat{\varsigma}}{\widehat{\beta}}\right)\right\}. $$

respectively.

Non-parametric estimation was calculated using the kernel method (Silverman 1986). Based on the above analysis, we determined the best model, thus calculating return periods. A T-year return period using x T represents the maximum value of t years (annual maximum daily rainfall). The calculation of the return period including \( F\left({x}_T\right)=1-\frac{1}{T} \) from model 1 yields the expression

$$ {x}_T=\mu -\frac{\beta}{\kappa}\left\{1-{\left[- \log \left(1-\frac{1}{T}\right)\right]}^{-\kappa}\right\} $$
(3)

Similarly, the T from model 2 is

$$ {x}_T=\varsigma -\beta \log \left\{- \log \left(1-\frac{1}{T}\right)\right\} $$
(4)

We entered \( \widehat{\varsigma} \),\( \widehat{\beta} \), and \( \widehat{\kappa} \) values into Eqs. (3) and (4) to calculate T values in models 1 and 2.

Confidence interval estimates are usually based on Delta or resampling techniques. Here, we used the profile likelihood method, which is generally considered superior to any other existing method (Kupferberg et al. 2012). The profile likelihood L p (x T ) calculation is given by

$$ {L}_p\left({x}_T\right)=\underset{\beta, \kappa}{ \max } L\left({x}_T,\beta, \kappa \right). $$

For x T of 100(1 − α)%, the confidence interval is set via

$$ \left\{\theta :2 \log \left(\frac{L\left(\widehat{\varsigma},\widehat{\beta},\widehat{\kappa}\right)}{L_p\left(\theta \right)}\right)\right\}<{\chi}_{1,1-\alpha}^2 $$

Here, \( {\chi}_{1,1-\alpha}^2 \) expresses the 100(1 − α)% quantile of the chi-squared distribution of freedom.

We selected sites at Beitashan, Yining, Urumqi, and Habahe to analyze this method. Let L i represent the maximum likelihood value of models 1 through 4, where i = 1, 2, 3, 4. Using model 1 estimates for Beitashan, we obtained \( \widehat{\varsigma}=17.14 \),\( \widehat{\beta}=6.77 \), \( \widehat{\kappa}=0.20 \), and −2 log L 1 = 360.68. Analogous model 2 estimates were\( \widehat{\varsigma}=18.23 \),\( \widehat{\beta}=7.02 \), and −2 log L 2 = 362.95. Thus, there were analog effects for model 2 but not for model 1. Figure 3 certifies the above conclusion. Figure 5 further illustrates the problem in which κ = 0 is not included in the confidence interval.

Fig. 3
figure 3

Fitted (solid line) and non-parametric (dotted line) densities for a model 1 (left) and b model 2 (right) concerning Beitashan

Full size image
Fig. 4
figure 4

QQ plot with simulated 95% confidence intervals for a model 1 and b model 2 concerning Beitashan

Full size image
Fig. 5
figure 5

K parameter log-likelihood profile in model 1 regarding Beitashan

Full size image
Fig. 6
figure 6

Spatiotemporal distribution of the estimated maximum daily precipitation over northern Xinjiang for various reoccurrence intervals (a 2 years, b 5 years, c 10 years, d 30 years, e 50 years, f 100 years) (unit: mm/day)

Full size image
Fig. 7
figure 7

Mean residual life plot of Urumqi precipitation data. Thresholds (u) vs. mean excess precipitation (unit: mm)

Full size image
Fig. 8
figure 8

a, b GPD fits for a range of 100 thresholds from 0 to 20 mm for the Urumqi precipitation dataset

Full size image
Fig. 9
figure 9

GPD fit diagnostic plots for Urumqi precipitation data using a threshold of 10 mm

Full size image
Fig. 10
figure 10

Log-likelihood profile plots for GPD with a 100-year return level (mm) and shape parameter (ξ) for Urumqi precipitation data

Full size image

We used models 3 and 4 to simulate Beitashan’s annual maximum daily rainfall. This produced − log L 3 = 179.73 − log L 3 = 179.73 and − log L 4 = 180.06, then − log 2L 3 = 359.46 and − log 2L 4 = 360.12, − log 2L 1/L 3 < 3.84, and − log 2L 2/L 4 < 3.84. We did not find that the time (year) of models 3 and 4 responded to significant trends. Models beyond 3 and 4 did not provide a significant fit. We compared models 1–8 in the same manner. We found no significant response to changing trends. Therefore, we concluded that model 1 was the most suitable (GEV distribution). The above analysis matches findings at other sites. Table 3 presents four examples of the site selection model, standard error, parameter values, and the Kolmogorov–Smirnov test results. Table 4 shows the example 5 estimate of the return period of the site T = 2.5, 10, 30, 50, and 100.

Table 3 Best-fitted models and parameter estimates
Full size table
Table 4 Return level estimates for T = 2, 5, 10, 30, 50, 100 years (unit: mm/day)
Full size table

The same approach was used for data related to 33 other sites, most of which were in accordance with model 1. Using model 1 for extreme precipitation (annual maximum daily rainfall), 37 meteorological stations in North Xinjiang gave T = 2.5, 10, 30, 50, and 100 years. Figure 6a–f shows kriging interpolation for 2, 5, 10, 30, 50, and 100-year spatiotemporal distributions of return periods. The distribution map of annual maximum daily rainfall revealed similar annual averages of both rainfall and precipitation in the mountains. Figure 6 shows that for T = 2 years, future precipitation is mostly greatly in excess of 18 mm/day. For T = 5 and 10 years, precipitation maxima in the Tianshan Mountains surpass 25 mm/day. For T = 30 and 50 years, most maxima are >35 mm/day. For T = 100 years, the maxima are <90 mm/day.

4.2 Generalized Pareto distribution (GPD) fitting

In contrast to GEV distribution, GPD describes the distribution of events exceeding a certain threshold (e.g., >20 mm of precipitation). This solves the problem of insufficient extreme precipitation data while increasing the use of existing information. However, in GPD fitting, determination of the threshold value is a key issue and major step. The mean residual life plot has served as a model to estimate an exploratory technology (Fig. 7). In this diagram, an approximately linear growth with large-amplitude fluctuations is observed. Appropriate thresholds are believed to occur in the linear growth trend at the end of the curve and ∼10 mm was optimum here. The 95% confidence interval is shown by a dashed line.

Alternatively, it is possible to calculate each time with different u threshold values. Changes can be estimated by determining stability in terms of scale and shape parameters of the maximum likelihood, as shown in Fig. 8. Similarly, the linear trend of the curve begins fluctuating toward the end of the defined threshold (10 mm). Figure 7 shows a statement conclusion, drawn from studies on threshold points of extreme precipitation (10 mm) in Urumqi.

We used the 10-mm threshold (the GPD fitting precipitation data from sites in Urumqi), diagnostic charts, and histograms to represent the observed data and curve-fitting model (Fig. 9). The regression level with 95% confidence interval is shown in Fig. 9. Over the entire period, there were a total of 371 days when precipitation exceeded the 10-mm threshold; with an annual average of 7.42 mm. Estimation of scale parameter value was \( \widehat{\sigma}=5.77 \) with a standard deviation of 0.43. The estimated shape parameter was \( \widehat{\xi}=-0.03 \) with a standard deviation of 0.05. The tail of the density map effectively shows the distribution of fitting observational data and models. The regression level is presented as a nonlinear curve, with its upper and lower curves on either side of the 95% confidence interval. Figure 10 depicts the configuration of the log-likelihood estimation, fitting the 100-year GPD T. T = 100-year corresponding to levels of 44.61 mm (38.20 left, 52.34 right), and the MLE estimate is \( \widehat{\xi}=-0.03 \) (−0.13, 0.09).

Estimates using the GPD and GEV fitting T levels for Urumqi are shown in Table 4, demonstrating similar fitting results for GPD and GEV. For shorter T, such as 2 and 5 years for estimated precipitation levels, GPD results at all sites were slightly better than those of GEV. For T = 10 years, the two methods showed very similar estimations, and for 30 years and longer, GPD was frequently greater than with GEV concerning Urumqi. For a 100-year T, precipitation reached 44.62 mm/day for GPD, greater than GEV at 40.83 mm/day, shown in Table 5. Similarly, results were gathered at other sites. GPD was much higher at most sites fitting the GEV level regression estimation. Based on precipitation data using the GEV distribution and GPD for 37 sites fitting the precipitation event, we obtained the parameter estimates; results differed slightly but remained similar overall. This is not covered in detail here.

Table 5 Return level estimates for T = 2, 5, 10, 30, 50, 100
Full size table

5 Summary

We applied GEV and GPD statistical distribution functions to fit the output of precipitation extremes with different T, to diagnose the risk of flood variability and associated spatial patterns in northern Xinjiang, China. Important results were obtained, as follows:

  1. 1.

    GEV extreme value modeling yielded the best results, proving to be extremely valuable. Through example analysis for extreme precipitation models, the GEV statistical model was superior for favorable analog extreme precipitation. The risk of flooding in northern Xinjiang has changed markedly. Aridity in the region has decreased prominently. CDD decreased at a rate of 1.7 days/10 years, while consecutive wet days increased at a lower rate of 0.1 days/10 years. This situation accords with the view that the climate in Xinjiang has been changing from warm-dry to warm-wet in recent years.

  2. 2.

    The GPD model calculation results reflect annual precipitation. The precipitation data found using a broad value theory distribution (GEV) and broad GPD for 37 sites during the precipitation event were close to the parameter estimates, and the results showed different values. For most of the estimated sites 2 and 5-year T for precipitation levels, GPD results were slightly greater than those of GEV. For T = 10 years, the two methods were very similar. For T = 30 years, and the regression cycle, the GPD fitting estimated much greater values than GEV. After more than 30 years, we found that the simulation results of the GPD model are better than that of the GEV model by linear regression. The GPD shows evidence of significant positive trends, indicating that the significance of the extreme precipitation in northern Xinjiang is sensitive to the method used. In addition, GDP would be able to predict the return value of this extreme rainfall event at a specific time in the future.

  3. 3.

    Based on the chosen models, we have provided return levels of the extreme precipitation (including intervals of return levels) for T = 2, 5, 10, 30, 50, and 100 years. From the spatiotemporal distribution diagram of extreme rainfall, extreme precipitation is increasing in northern areas, particularly in the mountainous areas of North Azerbaijan. For example, Tianchi shows evidence of increased significance trends in the southeast of the investigated area. In the northern Xinjiang area, precipitation values, extreme rainfall, and flood disaster events were compared. The study found that extreme precipitation that reaches a certain limit value level will cause a flood disaster. Therefore, predicting future extreme precipitation may aid in predictions of flood disasters. The results of this study may serve as a useful reference for future studies regarding early-warning systems for flood disasters.