Swept and curved wings: a numerical approach based on generalized lifting-line theory

Abstract

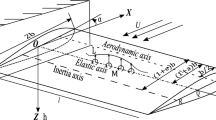
 Whenever the lifting-line is used for curved and swept wings with high aspect ratios, available software shows weaknesses. Actually, when considering sweep and curvature, most of these programs use the normal component of the incident flow in an empirical extension of Prandtl's model, which is theoretically founded only in the case of straight unswept wings. Recent theory based on the matched asymptotic expansions technique shows that, in addition to this 2D-type correction, extra terms have to be considered in order to express the three-dimensional induced velocity, when computing the spanwise variation of the circulation. These terms require finite parts in Hadamard's sense integrals computation. On these theoretical foundations, the computational approach presented in this paper improves on the empirical approach for swept, curved lifting-lines, including all the necessary corrections. The validity of the approach is examined in a simple application compared with available analytical and numerical results. Considering these results, it can be said that the model described here offers real improvements over the usual empirical numerical computations for arbitrarily shaped lifting-lines.