Tuning quantum cascade laser wavelength by the injector doping

Abstract

Tuning the wavelength of emitted radiation is a tremendous feature of quantum cascade lasers which enables their use in various applications. Usually, this tuning is executed by the change of the bias current or the temperature. In this paper, it is demonstrated, both experimentally and theoretically, that yet another possibility of tuning laser wavelength offers the change of doping density. For the experimental demonstration, a set of GaAs/AlGaAs devices emitting in the range 9.3–9.7 µ${\rm {m}}$ was MBE grown and processed. For the theoretical analysis, the simulations that employ nonequilibrium Green’s function formalism, applied to the single-band effective mass Hamiltonian, are used. The analysis shows that the physical mechanism responsible for wavelength-doping correlation is a linear Stark effect. The range of tuning is limited on both low and high doping side. Both these limits are established and discussed.

1 Introduction

The well-known feature of a quantum cascade laser (QCL), which enables this device being used in gas tracing systems, is the possibility of tuning the wavelength of the emitted radiation. The wavelength of a QCL is tuned by changing either the laser temperature and/or the bias current [1]. Temperature tuning provides a broad tuning range; however, it is slow as the whole submount and laser needs to be temperature-controlled. Through the use of a buried heater element, the active region temperature can be modified without changing the submount one. This method has been successfully applied to buried heterostructure lasers, becoming an attractive solution for molecular spectroscopy [2]. The short period length and the diagonal nature of the laser transitions in QCLs guarantee an additional tuning mechanism of the emission due to the linear Stark effect [3].

The influence of doping density on the performance of QCLs, working in mid-infrared (MIR) range, has been studied mainly in the context of dynamic working range and efficiency [4,5,6,7,8], with only a limited number of experimental investigations, undertaken to clarify its influence on emission characteristics [9]. While, for the obvious reasons, this method cannot be used for tuning devices mounted onboard the sensing systems, it seems attractive for the preselection of the spectral range when designing devices dedicated for specific applications. In this paper, this possibility is demonstrated both experimentally and theoretically. The basic theoretical tool employed in the analysis is numerical modeling. It is shown that the Stark shift is the physical mechanism responsible for the observed phenomenon, which otherwise is limited to the certain range of doping densities.

2 Experiment

Experiments were performed with the GaAs/Al_0.45Ga_0.55As devices that utilize resonance phonon depopulation scheme. The 3-well active region design of [10, 11] was adopted: the layer sequence in the single QCL module was: 4.6, 1.9, 1.1, 5.4, 1.1, 4.8, 2.8, 3.4, 1.7, 3.0, $\underline{\mathbf{1.8}}$, $\underline{2.8}$, $\underline{\mathbf{2.0}}$, $\underline{3.0}$, 2.6, 3.0 nm, starting from the injection barrier. The AlGaAs layers are denoted in bold. The underlined layers are n-doped. The injector doping was in the range $3.4 \times 10^{17}$ to $8.0 \times 10^{17}\,\text {cm}^{-3}$. Only two-barrier quantum well pairs in the central part of each injector were doped. The structure containing 36 modules was grown by MBE. TEM image and schematics of the grown structure are shown in Fig. 1.

Fig. 1

a Structure of GaAs/AlGaAs QCL, b TEM image of a few periods of the active region. The $\text {Al}_{0.45}\text {Ga}_{0.55}\text {As}$ barrier layers give darker contrast; the GaAs wells are brighter

The structure used a double-plasmon Al-free waveguide for planar optical confinement. The core of the structure was embedded in the lightly doped waveguide composed of 3.5 µm thick n-GaAs layers on each side ($n = 4.0\times 10^{16}\,\text {cm}^{-3}$), terminated by 1 µ${\rm {m}}$ thick highly Si-doped ($n = 1.0\times 10^{19}\,\text {cm}^{-3}$) GaAs layers. For such a waveguide, the optical losses and the confinement factor were estimated in the range $\alpha _\mathrm{{w}}=$16–20 $\; \text {cm}^{-1}$ and ${\Gamma }=0.31$, respectively [12]. The double trench lasers with 3 mm $\times \;25$ µm current windows were fabricated using standard processing technology [13]. The facets were uncoated, so the mirror losses can be estimated as $\alpha _\mathrm{{m}}\cong 5\,\text {cm}^{-1}$.

In the experiment, only the injector doping was subjected to the variation: the devices doped to different density $N_{\text {dop}}$ in the range 3.4–8.0 $\times 10^{17} \; \text {cm}^{-3}$ were fabricated and characterized. Current–voltage–light characteristics and lasing spectra were measured. For the latter, the experimental strategy was to keep the parameters, which are known to influence the wavelength, constant. In QCLs, the lasing takes place for the current density J above the threshold value $J_{\text {th}}$. The threshold current is known to depend quite a bit on doping density at high temperatures [4, 6], and much more weakly at low temperatures [5, 6, 8]. This is because the major gain-deteriorating mechanism is thermal backfilling of lower laser state [14]. At high temperatures, the distribution of electrons that occupy injector states has a long energy tail reaching the lower laser state. Then, the increasing doping results in the increasing filling of this state and decreased population inversion. At low temperatures, the redistribution of the electrons, due to the increasing doping, is limited to the injector states, so the population of the lower state is not so much affected [13, 14]. Data in Fig. 2, collected for our devices, are in full correlation with this scenario: the threshold current remains practically unchanged when $T < 100$ K, while at higher temperatures, it depends strongly on doping density. Making the planned experiment above $T> 100$ K may then result in a disappearance of the lasing when the threshold current exceeds the measurement current. Therefore, our experimental temperature was fixed at 77 K, at which the threshold current hardly depends on the doping density. The devices were also chosen to have similar characteristic temperature $T_{0}$, regardless of doping (see Fig. 2).

The condition $J=\text {const}>J_{\text {th}}$ was fulfilled assuming $J=1.5 J_{\text {th}}\cong 6.0 \; \text {kAcm}^{-2}$. The emission spectra of lasers with different injector doping densities, together with their L–I–V characteristics, are shown in Fig. 3. The internal differential quantum efficiency of the devices appears to depend on doping density in a systematic manner: it drops from 40% for the lowest doped device to 13% for the highest doped device. The wavelength-doping correlation is also clear; the red shift of the spectra is observed with the increasing injector doping. Roughly $50 \; \text {cm}^{-1}$ shift of the emission spectrum is recorded for the doping range investigated. To ensure that the observed shift cannot be attributed to any thermal effect, the latter was carefully studied, like in [15]. For 200 ns pulse duration used in the experiment, the registered, thermal-induced wavelength shift during the pulse was ${\Delta }\lambda =5.44\;\text {nm}\;\left(0.619\;\text {cm}^{-1}\right)$ which is almost 2 orders of magnitude lower than the one caused by the changing doping.

Fig. 2

Threshold current density vs. injector doping. Characteristic temperature $T_{0}$ for data series are: 100, 107.5, 93.9 K for doping densities: $4, 6, 8 \times 10^{17} \; \text {cm}^{-3}$, respectively. Inset: temperature dependence of the threshold current at 77 K

Fig. 3

a L–I–V characteristics and b the emission spectra for GaAs/AlGaAs QCLs doped to different densities measured with 200 ns pulse duration and 5 kHz repetition. The lasers are otherwise identical

3 Model

QCL is the unipolar n-type device, so the theoretical analysis can be limited to a one-band Hamiltonian. For stratified devices, there is a translational symmetry in-plane of the layers, which allows for further simplification to one-dimensional (1D) Hamiltonian parametrized for the in-plane momentum k. The full non-interacting effective mass Hamiltonian reads:

$$\begin{aligned} H(k)=\frac{-\hbar ^2}{2}\frac{d}{dz}\frac{1}{m(E,z)}\frac{d}{dz}+V(z)+\frac{\hbar ^2k^2}{m(E,z)}, \end{aligned}$$

(1)

where the potential energy $V(z)=E_{c}(z)+eU+V_{sc}(z)$ comprises the conduction band (CB) edge profile $E_{c}(z)$, the external bias U, and the mean field term $V_{sc}(z)$. Although Eq. (1) is strictly one-band Hamiltonian, it accounts for mixing with remote (valence) bands through energy-dependent effective mass, $m(E,z)=m^{*}(z)\left\{ 1+[E-E_{c}(z)]/E_{g}(z)\right\}$. The in-plane dynamics included by kinetic energy terms uses the same mass, m(E, z). It was shown that such a formulation preserves the in-plane non-parabolicity, comparable to the results predicted by the 8-band $\text {k}\cdot \text {p}$ method [16]. The Hamiltonian of Eq. (1) was used with nonequilibrium Green’s function (NEGF) formalism to get the reliable results which account for both quantum coherence and scattering. The use of this method is a must as our conclusions (to be presented further on) relay on the estimation of the gain peak magnitude, which in this method is calculated without any simplifying assumptions. In other methods, this value may depend on somewhat arbitrary assumed broadening [17].

In our approach, the equations of NEGF formalism were solved numerically in the real space. To maintain the sub-nanometer precision of QCL layers and simultaneously keep numerical load within reasonable limits, the structure was mapped onto a non-uniform mesh [18,19,20]. Only a portion consisting of one module + one more well and barrier was discretized; the rest of the cascade was mimicked by the contact self-energies [21,22,23]. Other self-energies included into the NEGF formalism account for scattering with: phonons (optical and acoustic), ionized impurities, interfaces roughness (IR), and alloy disorder. Electron–electron interactions were included through the mean field calculated by the solution of the Poisson equation. Out of all self-energies included into NEGF formalism, only those for IR scattering contain some arbitrary parameters, related to islands rms height h and average diameter ${\Lambda }$. These are hardly measurable quantities and usually are evaluated by adjusting experimental and calculated characteristics [24]. Such a procedure applied to our devices gives $h=0.19$ nm and ${\Lambda }=9$ nm. Similar values are reported in the literature, e.g., in [25]. Reasonable estimation of the h and ${\Lambda }$ values is further confirmed by the calculations of optical gain presented in Figs. 4 and 5. The gain was calculated with the use of theory presented in [26] in the first order approximation, i.e., the terms $\delta {\Sigma }$ were ignored.

Fig. 4

a Gain spectra and b gain peak wavelength calculated for devices with injectors doped to different densities (line and symbols) compared to the experiment (shaded area)

4 Results and discussion

In general, a good qualitative agreement between the calculated gain and the experiment is found. Namely: (i) the gain spectra of Fig. 4 peak at the frequency $h\nu$ that corresponds well to the experimental lasing wavelength $\lambda$; (ii) gain peak moves to lower frequencies (higher wavelengths) when doping density increases; (iii) the ranges of tuning densities 3–8 $\times 10^{17} \; \text {cm}^{-3}$ agree quite well; (iv) the sensitivity $\sim 0.4\,$ µ${\rm {m}} {/} 5 \times 10^{17} \; \text {cm}^{-3}$ of the lasing wavelength to the change of doping densities is well reproduced; (v) the calculated FWHM $\cong 15$ meV of the gain spectra agrees with the reported FWHM $\cong 12$ meV of the electroluminescence [10]; (vi) gain peaks reach the value of $~ 100 \; \text {cm}^{-1}$ which is well above the threshold value $(\alpha _{\text {w}}+\alpha _{\text {m}})/ {\Gamma } \cong 60 \; \text {cm}^{-1}$ as expected for the experimental current $J=1.5J_{\text {th}}$. The value of gain peak does not change with doping what can be a source of important conclusions. For the 3-well, device with the states numbered in the down–up order, the gain can be expressed as

$$\begin{aligned} g=g_{c}(n_{3}-n_{2})-\alpha _{\text {ISB}}, \end{aligned}$$

(2)

where $g_{c}$ is the gain cross section, $\alpha _{\text {ISB}}$ is the intersubband absorption, and $n_{i}$ are the populations of laser states. The independence of the gain peak on the doping density observed in Fig. 4a suggests that all these quantities do not change under the experimental conditions (constant current and temperature). As the populations are the function of current (which is kept constant) and the lifetimes, e.g., $n_{3}=J\tau _{3}/e$, the conjecture of doping independence can be extended on all involved lifetimes. In QCL, the transport is governed by the scattering-assisted resonant tunneling through the injection barrier, which is well described by the Kazarinov–Suris formula [27]:

$$\begin{aligned} J=en_{\text {g3}}\frac{2| {\Omega }_{\text {g3}}|^{2}\tau _{||}}{1+ {\Delta }^{2}\tau ^{2}_{||}+4| {\Omega }_{\text {g3}}|^{2}\tau _{3}\tau _{||}}, \end{aligned}$$

(3)

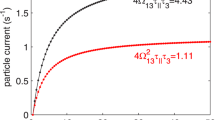
where $\tau _{||}$ is the dephasing time and ${\Omega }_{\text {g3}}$ is the coupling strength of the states involved in the transition, i.e., the laser upper state 3 and the ground injector state g. Similar to the lifetime $\tau _{3}$, these quantities hardly depend on the doping density. On the contrary, the sheet density $n_{\text {g3}}$ of the carriers shared by the states 3 and g increases with the doping density. To keep the current J constant, this increase must be compensated by the increased detuning from the resonance ${\Delta }$. This mechanism is illustrated in Fig. 5.

Fig. 5

Current–voltage characteristics predicted by Eq. (3) for several doping densities (lines) together with the results of NEGF simulations (symbols)

The I–V characteristics plotted according to Eq. (3) were compared to the simulations. While drawing the lines, a linear relation between $n_{\text {g3}}$ and $N_{\text {dop}}$, and ${\Delta }=V_{\text {res}}-V$, with $V_{\text {res}}=10$ V, was assumed. The horizontal line is pinned to the value of the constant current density $J \approx 1.5 J_{\text {th}}=5.5 \; \text {kAcm}^{-2}$. As can be seen, both Eq. (3) and the results of simulation predict a decrease of the bias voltage V with increasing doping density. This was also observed in the experiment (see Fig. 3a). The decreased V transfers then to the decreased separation $E_{3}-E_{2}$ of laser levels and so the energy $h\nu =E_{3}-E_{2}$ of emitted photons through the linear Stark effect.

In the range 2–6 $\times \; 10^{17} \; \text {cm}^{-3}$ of doping densities, the results of the simulations follow closely the lines predicted by Eq. (3). It ensures that the assumption about a linear relation between $n_{\text {g3}}$ and $N_{\text {dop}}$ is reasonable in that range of doping density. Situation changes for the higher doping: for $N_{\text {dop}}= 12 \times 10^{17} \; \text {cm}^{-3}$ the simulation predicts much lower detuning from the resonance than predicted by Eq. (3). The reason for this is that the lower percentage of carriers takes part in the tunneling though the injection barrier. In Fig. 6b, the distributions of electrons within QCL module are compared for two doping densities: $N_{\text {dop}}= 2 \times 10^{17} \; \text {cm}^{-3}$ and $N_{\text {dop}}= 12 \times 10^{17} \; \text {cm}^{-3}$.

Fig. 6

a Conduction band edge and b distribution of electrons within one QCL module calculated self-consistently by the solution of NEGF and Poisson equations with the boundary conditions that preserve charge neutrality of the single QCL module. Devices were doped to $12 \times 10^{17} \; \text {cm}^{-3}$ (thick, blue line) or $2 \times 10^{17} \; \text {cm}^{-3}$ (thin, red line). Slope of the straight lines shows the average field in the whole structure (dotted line) or the local field in active wells (dashed line) for the device doped to higher density

The center of the mass of the ground injector state is located in the injection well. Carriers occupying this state and upper laser state contribute to the density $n_{\text {g3}}$. For the lower doping, the electrons reside mostly in the injection well and greatly contribute to $n_{\text {g3}}$. For the higher doping, the electrons reside mostly in the well left-preceding the injection well, and therefore, the percentage of carriers contributing to $n_{\text {g3}}$ is lower. Then, lower detuning ${\Delta }$ is necessary to compensate increase of $n_{\text {g3}}$ (caused by the increased doping). This effect may explain the lowering sensitivity of the lasing wavelength to the changing doping when the latter goes to higher densities, what can be observed in the simulation curve in Fig. 4b. However, it cannot explain the complete saturation of this curve. This must be attributed to substantial band bending occurring for the highest doping densities. When doping increases, then, according to Eq. (3), the bias voltage U must decrease to keep the current constant. At low doping densities, there is little band bending, and so the local field in active wells, $F_{\text {a-w}}$, equals approximately the mean field $\left\langle F \right\rangle =U/L$, where L is the length of the structure. Then, the energetic separation of laser levels, $E_{3}-E_{2}$, decreases due to the linear Stark effect. With the increasing doping, the bands bend upward in the injector wells, where most of the charge is accumulated. Therefore, the field in the remaining (active) wells must be higher than the average field, $F_{\text {a-w}}> \left\langle F \right\rangle$. This means that when doping increases (bias voltage decreases), $F_{\text {a-w}}$ drops less than $\left\langle F \right\rangle$ (see Fig. 6a). Consequently, the Stark shift is less sensitive to the increasing doping when the latter goes to large values. Our numerical simulations show that, with further increase of the doping, the field in the active wells, $F_{\text {a-w}}$, stops decreasing at all, but instead saturates at certain minimum value. This causes saturation of the Stark shift for the highest doping, observed both in Fig. 4b (experiment) and Fig. 7 (simulations), and simultaneously defines the lower limit of the frequencies that can be reached by changing doping density. The upper limit of frequency tuning is more trivial: for the doping, as low as $1 \times 10^{17} \; \text {cm}^{-3}$, there are not enough carriers to reach the experimental current (see Fig. 5), or even the threshold current required for lasing.

Fig. 7

Difference between upper and lower laser level energies $E_{3}-E_{2}$ as a function of bias voltage, calculated for self-consistent potential (line + symbols) or assuming constant field in the whole structure (line). The self-consistent potential was calculated for the doping density which preserves the experimental condition, i.e., constant current density of $J=1.5J_{\text {th}}$

5 Conclusions

In this paper, we have characterized in detail QCL wavelength tuning by the injector doping. A rigorous model of the observed effect, based on nonequilibrium Green’s function formalism, has been presented. The physical mechanism responsible for this phenomenon is the linear Stark effect. The range of tuning is limited on both low and high doping sides. On the low doping side, the limitation is caused by the insufficient free carrier density to reach the threshold current/gain. On the high doping side, the tuning is limited by: (i) the saturation of the Stark shift caused by band bending and (ii) the decreased efficiency of carrier injection due to their redistribution caused by strong attraction of the dopants. The phenomenon can be utilized for the rough tuning of devices wavelength, dedicated to operate in the specific frequency bands.

Although the analysis was performed exclusively for GaAs-based devices, it is highly probable that it can be fully applicable to more efficient InGaAs/AlInAs/InP QCLs. This is confirmed by the laser spectra provided in Fig. 8 which exhibit identical doping-emission wavelength correlation. On the other hand, the data presented in [9] for short-wavelength InP-based QCLs seem to contradict this conjecture: the decrease of wavelength was observed with the increasing doping. Although it was postulated that this can be due to some complex thermal effect, the interpretation in terms of the current model is still possible (and much more straightforward): the measurements in [9] were done for the currents “slightly higher than the threshold current” which in their devices changed by 55% (from 1.95 to $3.02\,\text {kAcm}^{-2}$) when doping increased merely by 28% (from 1.68 × 10¹⁷ to $2.07\,\times 10^{17}\,\text {cm}^{-3}$). According to Eq. (3), this difference must have been compensated by the simultaneous decrease of detuning from resonance ${\Delta }$, that is an increase of the bias voltage (see Fig. 5). Then, the associated Stark effect leads to the observed blueshift of the lasing frequency. Unfortunately, in [9], the I–V characteristics were not provided, so drawing definite conclusions on the physical mechanism, responsible for tuning the laser wavelength by the injector doping in InP-based devices, must be left for future studies.

Fig. 8

Emission spectra measured for InGaAs/AlInAs/InP QCLs doped to different densities