Design Weaknesses in Recent Ultralightweight RFID Authentication Protocols

Abstract

In this paper we focus our attention on the design of several recently proposed ultralightweight authentication protocols and show that the underlying methodology is not sound. Indeed, the common feature of these protocols lies in the use of transforms, which are the main building blocks. We analyze these transforms and show that all of them present some weaknesses, which can be essentially reduced to poor confusion and diffusion in the input-output mappings. Then, exploiting the weaknesses of the transforms, we describe impersonation attacks against the ultralightweight authentication protocols in which they are used: precisely, RCIA, KMAP, SLAP, and SASI$^{+}$. On average, an attack requires a constant number of interactions with the targeted tag, compared to the allegedly needed exponential number in the informal security analysis. Moreover, since the weaknesses are in the transforms, the attack strategies we describe can be used to subvert any other protocol that uses the same transforms or closely-related ones.

1 Introduction

Motivations for the Current Work. Secure authentication is a well-established research area in cryptography and several good solutions are available and used every day. Unfortunately, for low-cost inexpensive computing elements, like RFID tags, it is quite a challenging problem. These protocols involve two parties: a Reader and a Tag, both of which are small devices. The hardware imposes very strong constraints on the computing capabilities of these elements, especially on the Tag. Hence, standard techniques based on public key cryptography or on symmetric key primitives cannot be employed in the design.

Due to the above constraints, there are two choices: either to give up because it is difficult, or probably impossible, to achieve the security standard we get with other, much more powerful, digital devices, or to try to achieve a reasonable security level also in applications using these cheap computing elements. It goes without saying that they are becoming a crucial end point of smart automated solutions in the so called Internet of Things. Thus, it is desirable to follow the latter option.

However, unfortunately, the current state of knowledge is quite poor: we do not have any impossibility result within a model for such ultralightweight protocols but, at the same time, all ultralightweight authentication protocols, designed according to ad hoc approaches, proposed in the last years, have been shown to suffer several weaknesses of different significance and impact: in many cases the weaknesses have been used to break the protocols.

In some papers warnings have been rised against such solutions. In [3] a full analysis of one of the most representative (at that time) ultralightweight authentication protocol was provided, and in general the limits of such approaches, not based on sound security arguments, were stressed. Moreover recently, in [2], a full guide to the common pitfalls which are usually present in the design of ultralightweight authentication protocols has been provided to designers and practitioners.

As a matter of fact, ad hoc protocols with informal security analyses continue to be presented at a considerable rate and they are broken quickly after publication¹. Compared to the first protocol proposals of a few years ago, the new feature which almost all newer protocols exhibit, is that some more involved transforms of the data stored in the tag memory are used in order to construct the messages the Reader and the Tag send to each other to be confident of the reciprocal identities. However, as for the earlier protocols, also for these, sort of generation 2.0 ultralightweight authentication protocols, the informal security analyses are based solely on the following, questionable and very weak, conclusion: since the transforms are complex, only the legitimate parties who share the secret keys can produce the correct messages required by the authentication protocol; for the same reason, no adversarial entity, without the secret keys, can be successful with non negligible probability, that is, the best attack that can be applied is to guess the secret keys, which belong to an exponentially large set. In other words the entire security proof, in most cases, reduces to the alleged complexity of the transforms.

Our Contribution. Among the many novel ultralightweight protocols appeared in the literature in the last two years, we concentrated our attention on: KMAP [5], RCIA [6], SASI$^{+}$ [7], and SLAP [4]. All these protocols base their security properties upon some transforms. Our attention was caught because they appear to be more structured, compared to other previous proposals. The transforms essentially try to protect their input values by masking them via a processing stage, in which some secret values are involved and elementary operations, allowed by the low-power computational devices, are applied. We have studied such transforms and pointed out that they achieve poor confusion and diffusion. Moreover, exploiting the weaknesses found, we construct impersonation attacks against KMAP, RCIA, SASI+ and SLAP, which reduce from exponential to constant the number of trials needed to an adversary to impersonate the Reader to a Tag. We remark that the results on the transforms can be used to attack any protocol based on them.

2 Preliminaries: Transforms

Let us look at the transforms used in the authentication protocols we are dealing with. Due to lack of space, all proofs are omitted from this abstract.

Pseudo-Kasami Codes. Pseudo-Kasami codes, used in [5], are defined as follows. Let $x=x_1,\ldots ,x_n$ be a string of n bits and let s be an integer, called seed, such that $1\le s \le n$. Let $y=\mathtt{CRshift}(x,s)$, where y is obtained from x by a circular right shift of s positions. Then, the pseudo-Kasami code of x is defined as $\mathtt{pKc}(x,s)=x \oplus y$. Here is an example, where $n=24$ and the seed $s=6$:

The following lemma holds:

Lemma 1

Let $x=x_1,\ldots ,x_n$ be a string of n bits, and let s be a seed for the pseudo-Kasami code $\mathtt{pKc}(x,s)$ such that n is a multiple of s. Let $x'$ be a new string obtained from x by flipping n / s bits, all at distance s from each other. Then $\mathtt{pKc}(x,s)=\mathtt{pKc}(x',s)$.

An example helps in understanding the above result. Let us consider the same bitstring x considered before, and let us apply the lemma starting from position $j=2$.

It is easy to check that $\mathtt{pKc}(x,s)$ and $\mathtt{pKc}(x',s)$ coincide.

Let $\mathtt{hw}(\cdot )$ denote the Hamming weight of a binary string, i.e., the number of bits equal to one. The following results also hold:

Lemma 2

Let $x=x_1,\ldots ,x_n$ be a string of n bits chosen uniformly at random, and let s be an integer chosen uniformly at random such that $1 \le s \le n.$ Moreover, let $x'$ be a new string obtained from x by flipping one bit. Then $\Pr [\mathtt{hw}(\mathtt{pKc}(x,s))=\mathtt{hw}(\mathtt{pKc}(x',s))]=\frac{n+1}{2n}$.

Lemma 3

Let $x=x_1,\ldots ,x_n$ be a string of n bits chosen uniformly at random. Let $x'$ be a new string obtained from x by flipping two randomly selected bits. Then, for any seed s such that $1\le s \le n$, it holds that:

• (a) $\mathtt{pKc}(x,s)$ and $\mathtt{pKc}(x',s)$ are equal with probability $\frac{1}{(n-1)}$

• (b) $\mathtt{pKc}(x,s)$ and $\mathtt{pKc}(x',s)$ differ in two bits with probability $\frac{n\cdot (n-2)}{n^2(n-1)}$

• (c) $\mathtt{pKc}(x,s)$ and $\mathtt{pKc}(x',s)$ differ in four bits with probability $\frac{n^3-3n+2}{n^2(n-1)}$

• (d) $\Pr [\mathtt{hw}(\mathtt{pKc}(x,s))=\mathtt{hw}(\mathtt{pKc}(x',s))]=\frac{3n^2 + 3n-2}{8n\cdot (n-1)}$.

Finally, the pseudo-Kasami code transform exhibits the following structural property:

Lemma 4

Let $x=x_1,\ldots ,x_n$ be a string of n bits chosen uniformly at random, and let the seed s be equal to n / 2. Then, $\mathtt{pKc}(x,s)$ is the concatenation of two equal substrings of n / 2 bits.

Recursive Hash. Recursive hash was defined in [6]. Let x be a string of n bits, $x=b_1,b_2,\ldots ,b_n$, and let $\ell$ and z be integers such that $\ell$ is a divisor of n and $z=n/\ell$. Moreover, let s be an integer value, called seed, such that $1\le s\le z$. Then, dividing x into z chunks $x_1,\ldots ,x_z$ of $\ell$ bits each, $x_i=b_{(i-1)\cdot \ell },b_{(i-1)\cdot \ell +1},\ldots ,b_{i\cdot \ell -1}$, and denoting with $\mathtt{Rot}(x,y)$ a right rotation of the string x by y positions², the recursive hash of x and s, denoted by $\mathtt{Rh}(x,s)$ for short, is defined as:

$$x_1\oplus x_s,\ldots ,x_{s-1}\oplus x_s, \mathtt{Rot}(x_s,\mathtt{hw}(x_s)), x_{s+1}\oplus x_s,\ldots , x_{\frac{n}{\ell }}\oplus x_s.$$

That is, each chunk $c_i$ of the recursive hash is the $\oplus$ of chunks $x_i$ and $x_s$, except for chunk $c_s$, which is equal to $x_s$ right rotated by its Hamming weight.

Let us look at an example: let $n=24$ and $x=100100 101011 110101 111110$. Moreover, let $\ell =6$ and, thus, $z=4$. We get:

Let the seed s be equal to 3. The selected chunk is $x_3=110101$ whose Hamming weight is $\mathtt{hw}(x_3)=4$. Hence, the right rotation of $x_3$ is 010111. The recursive hash $\mathtt{Rh}(x,s)$ is:

Lemma 5

Let $\ell , n$ and z integers such that $\ell$ is a divisor of n and $z=n/\ell .$ Moreover, let $x=x_1,\ldots ,x_n$ be a string of n bits chosen uniformly at random, and $x'$ be a new string obtained from x by flipping two randomly selected bits. Then, for any seed $s\in \{1,\ldots , z\},$ $\mathtt{Rh}(x,s)$ and $\mathtt{Rh}(x',s)$ differ in two bits with probability equal to

$$ \frac{(n-\ell )(n-\ell -1)}{n(n-1)}. $$

Notice that the probability function is decreasing in $\ell$. Since meaningful values of $\ell$ range from 2 to n / 2, we have that the minimum value is obtained for $\ell =\frac{n}{2}.$ Therefore, for $\ell =\frac{n}{2}$, it is $\approx \frac{1}{4}.$

Lemma 6

Let $\ell , n$ and z integers such that $\ell$ is a divisor of n and $z=n/\ell .$ Moreover, let $x=x_1,\ldots ,x_n$ be a string of n bits chosen uniformly at random, and $x'$ a new string obtained from x by flipping two randomly selected bits. Then, for any seed $s\in \{1,\ldots , z\},$ $\Pr [\mathtt{hw}(\mathtt{Rh}(x,s))=\mathtt{hw}(\mathtt{Rh}(x',s))]$ is at least

$$\begin{aligned} \frac{1}{2}\cdot \frac{(n-\ell )(n-\ell -1)}{n(n-1)}+ \left( \frac{1}{2}\right) ^z\cdot \frac{\ell (\ell -1)}{n(n-1)}+ \frac{1}{2}\cdot \frac{n-\ell }{n}\cdot \frac{1}{n-1} \cdot \frac{{z-1 \atopwithdelims ()(z-1)/2}}{2^{(z-1)}}+ \frac{1}{2}\cdot \frac{n-\ell }{n}\cdot \frac{\ell -1}{n-1} \cdot \frac{{z+1 \atopwithdelims ()(z+1)/2}}{2^{(z+1)}}.\end{aligned}$$

A simple study of the function (for example with a math program like Maple), shows that it is an increasing function. Since meaningful values of $\ell$ range from 2 to n / 2, we have that the minimum value is obtained for $\ell =2.$ For $n=64$ the above probability is $\approx \frac{1}{2}$.

Conversion Transform. In [4] the authors introduce the $\mathtt{Cnv}$ transform. It takes as input two binary strings of length n, say³ $A=a_na_{n-1}\ldots a_2a_1$ and $B=b_nb_{n-1}\ldots b_2b_1$, and a threshold t such that $1\le t\le n$, and produces in output a binary string $\mathtt{Cnv}(A,B,t)$ of length n by applying a three-step procedure. More precisely:

Step 1 (Grouping). Determine a bit grouping for both A and B. The grouping is a function of the Hamming weight of the string and of the threshold t. Let $X=x_nx_{n-1}\ldots x_2x_1$ be the binary string to be bit-grouped. The grouping is defined recursively as follows: if the length of X is strictly shorter than t, then the recursion ends; otherwise, the string is split in two groups $X_L$ and $X_R$ according to its Hamming weight $w=\mathtt{hw}(X)$, by letting $X_L=x_nx_{n-1}\ldots x_{w+1}$, the $n-w$ leftmost bits, and $X_R=x_wx_{w-1}\ldots x_1$, the w rightmost bits. Then, the bit grouping procedure is applied recursively to both $X_L$ and $X_R$.

Let us consider an example. Let $n=24$, $X=1011\ 0101\ 1111\ 1101\ 1101\ 1101$ and $t=6$. The Hamming weight of X is $\mathtt{hw}(X)=18.$ Since $|X|\ge 6$, the string is split into two substrings, the left one, $X_1$, containing the leftmost $24-18=6$ bits, and the right one, $X_2$, containing the rightmost 18 bits of X; that is, $X_1=1011\ 01$ and $X_2=01\ 1111\ 1101\ 1101\ 1101$.

Since $|X_1|\ge 6$, and $\mathtt{hw}(X_1)=4$, the string is split in $X_{1,1}=10$ and $X_{1,2}=11\ 01$. Both strings are shorter than the threshold 6. Hence, the recursion ends.

We proceed similarly for $X_2$. Since $|X_2|\ge 6$, and $\mathtt{hw}(X_2)=14$, the string is split in $X_{2,1}=0111$ and $X_{2,2}=11\ 1101\ 1101\ 1101$. The recursion ends for $X_{2,1},$ while $X_{2,2}$ is split in $X_{2,2,1}=111$ and $X_{2,2,2}=101\ 1101\ 1101$. Since $X_{2,2,1}$ is shorter than $t=6$, then the recursion ends, while $X_{2,2,2}$ is split into $X_{2,2,2,1}=101$ and $X_{2,2,2,2}=1101\ 1101$. Thus, the recursion ends for the first substring, while it keeps going for the second. Indeed, since $\mathtt{hw}(X_{2,2,2,2})=6$, then $X_{2,2,2,2}$ is split in $X_{2,2,2,2,1}=11$ $X_{2,2,2,2,2}=01\ 1101.$ Finally, $X_{2,2,2,2,2}$ is split in $X_{2,2,2,2,2,1}=01$ and $X_{2,2,2,2,2,2}=1101.$

In the following table we report another example in a more concise form: the vertical lines indicate the splittings of the substrings. The starting string is $X=101101010101110101011111.$

Step 2 (Rearrangement). Once both A and B have been bit-grouped, the rearrangement phase simply swaps the two groupings, that is, the grouping found for A is applied to B and vice versa. Notice that the groupings might differ both in the number of groups and in the size of each group.

Let us continue with an example.

Let $A=1011\ 0101\ 1111\ 1101\ 1101\ 1101$ and $B=1011\ 0101\ 0101\ 1101$ $0101\ 1111$ be the strings that we have used as examples before. The grouping obtained for each of them is summarized in the following tables.

Swapping the groupings we get:

At this point each group of bits gets (left circularly) rotated according to the Hamming weight of the group itself. Thus we obtain:

Step 3. The final step that produces the output bitstring is simply the $\oplus$ of the rearranged bitstrings $A'$ and $B'$. Completing our example, we have:

We prove the following result:

Lemma 7

Given two binary strings A and B of length n, chosen uniformly at random, and a threshold t, with $1 < t \le n$, if we flip two bits of A in the first t positions to obtain $A'$, then

$$\Pr [(\mathtt{Cnv}(A,B,t), \mathtt{Cnv}(A',B,t)) \text {differ in two bits}] \approx \frac{1}{2} \cdot \frac{1}{6} \cdot \frac{t^3-2t^2-t+2}{t(t-1)^2}$$

3 KMAP

The protocol KMAP, introduced in [5], is a mutual authentication protocol. According to the authors, “KMAP avoids unbalanced logical operations (or, and) and introduces a new ultralightweight primitive, the pseudoKasami code, which enhances the diffusion properties of the protocol messages and makes the Hamming weight of the secrets unpredictable and irreversible". The protocol is also claimed to be “highly resistive against all possible attacks" and efficient in terms of communication cost and computational operations.

In this section we show that this is not the case. By building on the previous analysis of the pseudo-Kasami transform, we construct an efficient impersonation attack.

Protocol Description. Tags are identified with a static identifier ID which however is never exposed. Instead, a sequence of changing “pseudonyms” IDS is used. Tag and Reader share the pseudonym IDS and two secret keys, $K_1$ and $K_2$; these values are updated upon each successful completion of a session of the protocol. To cope with desynchronization attacks, the Tag and the Reader maintain both the current values and the previous ones. If a Tag receives twice the initial “Hello” message (see below), then the first time it replies with the current value of IDS , while the second time falls back to the old value, assuming that there has been a desyncronization with the Reader, which has been unable to recognize the newer value.

Hence, Tag and Reader maintain two triples of values: $({ IDS}_{cur}, K_{1,cur},$ $K_{2, cur})$ and $({ IDS}_{old}, K_{1,old}, K_{2, old})$. For the sake of simplicity of notation, sometimes, to save space, we omit the subscript of IDS, $K_1$ and $K_2$ when we are referring to the current values ${ IDS}_{cur}, K_{1,cur}$ and $K_{2, cur}$.

Fig. 1.

KMAP general structure

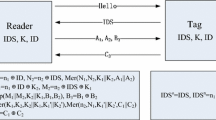
The protocol is a four-message protocol whose general structure is shown in Fig. 1:

• 1. The Reader starts the protocol by sending an “Hello” message;

• 2. The Tag replies with the current value of the identifier ${ IDS}_{cur}$;

• 3. The Reader checks the received value IDS : if it is equal to ${ IDS}_{cur}$, then the rest of the computation is performed using $K_1=K_{1,cur}$ and $K_2= K_{2, cur}$; if the received value is equal to ${ IDS}_{old}$, then the rest of the computation is performed using $K_1=K_{1,old}$ and $K_2= K_{2, old}$ – that is, the old values become the current ones; otherwise, the protocol is immediately terminated. The Reader performs some computation, computing some temporary values (a seed and two temporary keys $K_1^*$ and $K_2^*$), and three sequences of bits, A, B and C, and sends a message consisting of three parts. A, B and C, which are sent to the tag;

• 4. The Tag checks that the values received are consistent with its own information (if not, the protocol is immediately terminated) and performs some computation to obtain a sequence of bits D, which is sent to the Reader.

Upon completion of a session of the protocol, both the Tag and the Reader update the values of ID and of the keys $K_1$ and $K_2$, storing in $({ IDS}_{old}, K_{1,old}, K_{2, old})$ the values of $({ IDS}_{cur}, K_{1,cur}, K_{2, cur})$, and updating the latter. The Tag maintains also a failure counter, so that if there are too many unsuccessful attempts, the Tag will stop its functionality for a while, in order to introduce delays into the attacks⁴.

The details of the computation of the messages A, B, C and D are shown in Fig. 2. More specifically, the Reader chooses two random values $n_1$ and $n_2$, and computes their xor $P=n_1\oplus n_2$ and a seed $s=\mathtt{hw}(P)\mod 64$. Then, A is computed by a double rotation of $n_1$, the first of a number of positions given by the weight of ${ IDS}\, \oplus \, K_1$, and the second of a number of positions given by the weight of $K_2$; similarly, B is computed by a double rotation of $n_2$, the first of a number of positions given by the weight of $K_2\,\oplus \, { IDS}$, and the second of a number of positions given by the weight of $K_1\oplus n_1$. The Reader, then, computes two temporary keys, $K_1^*$ and $K_2^*$, namely $K_1^*=\mathtt{Rot}(\mathtt{pKc}(K_1,s),\mathtt{pKc}(n_1,s))\oplus K_2)$ and $K_2^*=\mathtt{Rot}(\mathtt{pKc}(K_2,s),\mathtt{pKc}(n_2,s))\oplus K_1)$, and, finally, computes C, again with a double rotation, namely $C=\mathtt{Rot}(\mathtt{Rot}(\mathtt{pKc}(n_1,s),\mathtt{pKc}(K_2^*\oplus \mathtt{pKc}(n_2,s)),\mathtt{pKc}(K_1^*,s)\oplus n_2))$. The message consisting of the concatenation of A, B, C is sent to the tag.

Fig. 2.

KMAP message computation

The Tag, upon reception of the message A||B||C, extracts the value of $n_1$ from A, by computing $n_1=\mathtt{Rot}^{-1}(\mathtt{Rot}^{-1}(A,K_2), \, { IDS}\,\oplus \, K_1)$, and $n_2$ from B, by computing $n_2=\mathtt{Rot}^{-1}(\mathtt{Rot}^{-1}(B,K_1\oplus n_1), \, { IDS}\,\oplus \, K_2)$, then computes $P=n_1\oplus n_2$, the seed s and the temporary keys $K_1^*$ and $K_2^*$. At this point, the Tag can compute the value of $C^*$ in the same way as the Reader computed C, and compare the computed value $C^*$ with the received one C. If they are equal, the Tag completes the protocol by computing and sending D and updating ${ IDS},K_1$ and $K_2$ as detailed in Fig. 3. On the other hand, if a mismatch is detected, then the protocol is aborted and the failure counter is incremented. The failure counter is reset when a session of the protocol is successful.

Fig. 3.

KMAP pseudonym and keys update

Impersonation Attack. Analyzing the equations used in the protocol, the following observations hold:

• 1. Flipping two bits of B is equivalent to flipping two bits of $n_2$ in some unknown positions.

• 2. Let $P'=n_1\oplus n'_2$, where $n'_2$ is equal to $n_2$ up to two flipped bits. Then $P'$ is equal to P up to two flipped bits. If the two flipped bits are the complement of each other, i.e., they are 01 or 10 respectively, we have that $\mathtt{hw}(P')=\mathtt{hw}(P)$. Since there are 2 out of 4 bit patterns that satisfy the above, this event occurs with probability 1 / 2.

• 3. If $\mathtt{hw}(P')=\mathtt{hw}(P)$, the structure of $\mathtt{pKc}(\cdot ,s)$ does not change since the seed is the same.

• 4. If $\mathtt{hw}(\mathtt{pKc}(n_2,s))=\mathtt{hw}(\mathtt{pKc}(n'_2,s))$, then the value $K^*_2$ does not change.

• 5. $\mathtt{pKc}(K^*_1,s) \oplus n'_2$ and $\mathtt{pKc}(K^*_1,s) \oplus n_2$ differs in two bits.

• 6. $\mathtt{hw}(\mathtt{pKc}(K^*_1,s) \oplus n'_2)=\mathtt{hw}(\mathtt{pKc}(K^*_1,s) \oplus n_2)$ with probability 1 / 2, since there are two patterns of bits, i.e., 01 and 10, such that, when flipped, the overall weight of the bitstring stays the same.

• 7. $\mathtt{pKc}(K^*_2,s) \oplus \mathtt{pKc}(n'_2,s)$ and $\mathtt{pKc}(K^*_2,s) \oplus \mathtt{pKc}(n_2,s)$ have the same weight with probability at least 3 / 8, since there are six patterns of four bits out of sixteen such that, when flipped, the overall weight of the bitstring stays the same.

Putting everything together, we can prove the following:

Lemma 8

Assume an adversary eavesdrops an authentication session and stores A||B||C. Let $B'$ be equal to B up to two bits which are flipped. Then, forcing the Tag to send the old IDS and replying with $A||B'||C$, the adversary succeeds in impersonating the legal Reader with probability roughly equal to $\frac{1}{28}.$

Thus, a few interactions are sufficient to break the security of the authentication protocol. Notice that, the authors specify that “a protocol message counter has also been integrated in the KMAP which stops the functionality of the Tag for some particular time, if the counter’s value exceeds the threshold 8”. It means that if the attack does not succeed during the first trials, an extra delay is added due to the temporary stop of the Tag.

4 RCIA

The protocol RCIA, introduced in [6], is a mutual authentication protocol. It has been designed to “provide robust confidentiality, integrity, and authentication in a cost effective manner". In RCIA, Tags use only three main operations, the bitwise and, or, and bit rotation, and the recursive hash transform scrutinized before.

Fig. 4.

RCIA message computation

Fig. 5.

RCIA pseudonym and keys update

Protocol Description. Since the protocol is very similar to the KMAP protocol, we describe it in a very concise way. The overall structure is the same as the one of KMAP (see Fig. 1): the differences lay in the way the messages A, B, C and D are constructed, and how the pseudonym and the keys are updated. The details of RCIA are described in Figs. 4 and 5.

Impersonation Attack. Analyzing the equations used in the protocol, the following observations hold:

• 1. Flipping two bits of B is equivalent to flipping two bits of $n_2$ in the same positions.

• 2. Let $P'=n_1\oplus n'_2$, where $n'_2$ is equal to $n_2$ up to two flipped bits. Then, $P'$ is equal to P up to two flipped bits. If the two flipped bits are the complement of each other, i.e., they are 01 or 10 respectively, we have that $\mathtt{hw}(P')=\mathtt{hw}(P)$. Since there are 2 good bit patterns out of 4 possible bit patterns, this event occurs with probability 1 / 2.

• 3. If $\mathtt{hw}(P')=\mathtt{hw}(P)$, the structure of $\mathtt{Rh}(\cdot ,s)$ does not change since the seed is the same.

• 4. If $\mathtt{hw}(\mathtt{Rh}(n_2,s))=\mathtt{hw}(\mathtt{Rh}(n'_2,s))$, then the values $K^*_2, \mathtt{Rh}(K^*_2,s)$ and C do not change.

Putting everything together, we prove the following:

Lemma 9

Assume an adversary eavesdrops an authentication session and stores A||B||C. Let $B'$ be equal to B up to two bits which are flipped. Then, forcing the Tag to send the old IDS and replying with $A||B'||C$, the adversary succeeds in impersonating the legal Reader with probability roughly equal to $\frac{1}{4}.$

Thus, a few interactions are sufficient to break the security of the authentication protocol.

5 SASI$^{+}$

The protocol SASI$^{+}$, introduced in [7], is a mutual authentication protocol. It incorporates only bitwise operations, xor, rotation and, like RCIA, the recursive hash transform. The protocol has also been implemented in hardware and shown to be efficient in terms of communication and computation costs.

Protocol Description. As for RCIA, also SASI$^{+}$, is basically the same as KMAP, with differences due to the way in which the messages are constructed and the way the pseudonym and the keys are updated. Figures 6 and 7 show the details.

Fig. 6.

SASI$^{+}$ message computation

Fig. 7.

SASI$^{+}$ pseudonym and keys update

Impersonation Attack. SASI$^{+}$ uses the recursive hash transform. Hence, applying a similar analysis to the one applied for RCIA, we notice that:

• 1. Flipping two bits of B is equivalent to flipping two bits of $n_2$ in some unknown positions.

• 2. Let $P'=n_1\oplus n'_2$, where $n'_2$ is equal to $n_2$ up to two flipped bits. Then, $P'$ is equal to P up to two flipped bits. If the two flipped bits are the complement of each other, i.e., they are 01 or 10 respectively, we have that $\mathtt{hw}(P')=\mathtt{hw}(P)$. Since there are 2 out of 4 bit patterns that satisfy the above, this event occurs with probability 1 / 2.

• 3. If $\mathtt{hw}(P')=\mathtt{hw}(P)$, the structure of $\mathtt{Rh}(\cdot , s)$ does not change since the seed is the same.

• 4. Due to Lemma 5, $\mathtt{Rh}(n_2,s)$ and $\mathtt{Rh}(n'_2,s)$ differs in two bits with probability at least $\frac{1}{4}$.

• 5. If this is the case, the resulting string $C'$ differs from C in two bits.

Putting everything together, the following result holds:

Lemma 10

Assume an adversary eavesdrops an authentication session and stores A||B||C. Let $B'$ and $C'$ be equal, respectively, to B and C up to two consecutive bits which are flipped. Then, forcing the Tag to send the old IDS and replying with $A||B'||C'$, the adversary succeeds in impersonating the legal Reader with probability roughly $\frac{1}{8}\cdot \frac{1}{96}.$

Thus, a linear (in the size of the bitstring) number of interactions is sufficient to break the security of the authentication protocol.

6 SLAP

The protocol SLAP, introduced in [4], is a mutual authentication protocol. It uses only bitwise operations like xor, rotations, and the conversion transform. The authors stress that the conversion transform is the main security component of the system “with properties such as irreversibility, sensibility, full confusion and low complexity", with better performance compared to previous protocols.

Protocol Description. As for the other protocols, the general structure is the same, although for SLAP the third message has a slightly different form. Figure. 8 shows the general structure of the protocol, while Figs. 9 and 10 provide the details. In SLAP the third message is composed of only two pieces, A and one half, either the left one or the right one, of B. The choice is determined by the Hamming weight of B itself: if it is odd, then $B_L$ is sent, otherwise $B_R$ is sent.

Fig. 8.

SLAP general structure

Fig. 9.

SLAP message computation

Fig. 10.

SLAP pseudonym and keys update

Impersonation Attack. Consider the $\mathtt{Cnv}(X,Y)$ function. The main observation is that by flipping two different bits of X at the beginning of X, the Hamming weight of the string stays the same, i.e., $\mathtt{hw}(X)=\mathtt{hw}(X')$ and, with high probability, $\mathtt{Cnv}(X',Y)$, where $X'$ denotes the modified bitstring, is different from $\mathtt{Cnv}(X,Y)$ in two bits. For example, in the example presented in [4], by flipping the second and the third bits of A, it follows that the final value $A^* \oplus B^*$ is modified only in the first and fourth bits. As we have formally shown before, such an event occurs in general with probability p approximatively equal to $\frac{1}{12}.$ Analyzing the equations of the protocol, notice that:

• 1. Flipping two bits of A is equivalent to flipping two bits of n in the same positions.

• 2. If the two flipped bits of n are complementary bits, i.e., 0 and 1 or 1 and 0, the resulting bitstring $n'$ is such that $\mathtt{hw}(n')=\mathtt{hw}(n)$ and, hence, $Rot(K_1,n')=Rot(K_1,n)$.

• 3. It follows that $\mathtt{Cnv}(Rot(K_1,n'), K_1\oplus K_2)=\mathtt{Cnv}(Rot(K_1,n), K_1\oplus K_2)$.

• 4. Since the bitstring $K_2 \oplus n'$ differs from $K_2 \oplus n$ in two bits, it follows that $Rot(\mathtt{Cnv}(K_2, K_2\oplus n'), K_1)$ differs in two bits from $Rot(\mathtt{Cnv}(K_2, K_2\oplus n), K_1)$ with probability $p\simeq \frac{1}{12}$.

• 5. The resulting string $B'$ differs in two bits from B and, with probability $\frac{1}{2}$, they have the same weight.

Putting everything together, the following result holds:

Lemma 11

Assume an adversary eavesdrops an authentication session and stores $A||B_{LorR}$. Let $A'$ be equal to A up to two consecutive bits which are flipped. Forcing the Tag to send the old IDS and replying with $A'||B_{LorR}$, the adversary succeeds in impersonating the legal Reader with probability roughly $\frac{1}{8}\cdot \frac{1}{12}.$

7 Conclusions

We have shown that the design of several recently proposed ultralightweight authentication protocols is affected by a common problem: the transforms, used as building blocks in the protocols, do not provide confusion and diffusion in the input-output mappings as they should. Exploiting the corresponding weaknesses, we have shown for example how impersonation attacks against the protocols can be mounted. Attacks defeating other properties of the schemes are possible (e.g., [8]). Moreover, we have not considered important practical issues in the implementation of ultralightweight protocols (e.g., [1]). Our goal was to point out that the lack of confusion and diffusion can open the door to several breaches. In the future proposals the designers should primarily check whether such basic properties are achieved by the underlying transforms. A closer look at the standard strategies used in the design of lightweight symmetric primitives might help. Actually, the most important open problem in our opinion is to come up with a reasonable model for the class of ultralightweight protocols, in order to get an in-depth understanding of possibilities and limits for these protocols.