Improvement of the energy resolution via an optimized digital signal processing in GERDA Phase I

Abstract

An optimized digital shaping filter has been developed for the Gerda experiment which searches for neutrinoless double beta decay in $^{76}$Ge. The Gerda Phase I energy calibration data have been reprocessed and an average improvement of 0.3 keV in energy resolution (FWHM) corresponding to 10 % at the $Q$ value for $0\nu \beta \beta$ decay in $^{76}$Ge is obtained. This is possible thanks to the enhanced low-frequency noise rejection of this Zero Area Cusp (ZAC) signal shaping filter.

1 Introduction

Gerda (GERmanium Detector Array) [1] searches for neutrinoless double beta decay ($0\nu \beta \beta$ decay) in $^{76}$Ge. The experiment is located at the underground Gran Sasso National Laboratory (LNGS) of INFN, Italy. Crystals made from isotopically modified germanium with a fraction of $\sim$86 % of $^{76}$Ge for a total mass of $\sim$20 kg are operated as source and detector of the process.

Several extensions of the Standard Model of particle physics predict the existence of $0\nu \beta \beta$ decay, a process which violates lepton number conservation by two units and which is possible if neutrinos have a Majorana mass component. $0\nu \beta \beta$ decay is therefore of primary interest in the field of neutrino physics. Neglecting the nuclear recoil energy the energy released by a $0\nu \beta \beta$ event is shared by the two emitted electrons. Both electrons are stopped within $\sim$1 mm of germanium and thus all available energy is deposited in a small region inside the detector. Since distortions by bremsstrahlung are expected to be small the $0\nu \beta \beta$ decay signature is a peak in the energy spectrum at the $Q$ value of the reaction, $Q_{\beta \beta }$, amounting to 2039 keV for $^{76}$Ge. The most recent result of this process for $^{76}$Ge was published by the Gerda collaboration with a 90 % confidence level (CL) limit on the $0\nu \beta \beta$ half-life of $T^{0\nu }_{1/2}>2.1\cdot 10^{25}$ year [2].

The sensitivity for detection of a possible $0\nu \beta \beta$ decay signal depends on the total efficiency $\varepsilon$ ($\simeq$75 % for Gerda Phase I), the enrichment fraction $f_{76}$ and the isotopic mass $m_A$ of the considered isotope, the total source mass $M$, the background level and the energy resolution. The expected number of signal events $n_S$ for a given half-life $T_{1/2}^{0\nu }$ is [3]:

$$\begin{aligned} n_S = \frac{1}{T_{1/2}^{0\nu }} \cdot \frac{\ln {2} \cdot N_A}{m_A} \cdot {f_{76}}\cdot \varepsilon \cdot M \cdot t \end{aligned}$$

(1)

where $N_A$ is the Avogadro number and $t$ the live time of the measurement. The expected number of background events $n_B$ within an energy window $\Delta E$ is:

$$\begin{aligned} n_B = BI \cdot \Delta E \cdot M \cdot t \end{aligned}$$

(2)

with $BI$ being the background index in cts/(keV$\cdot$kg$\cdot$year). The size of $\Delta E$ is proportional to the energy resolution at $Q_{\beta \beta }$, expressed as full width at half-maximum (FWHM). The energy resolution is of primary importance for the enhancement of the sensitivity and the modeling of background sources. If the event waveforms are fully digitized with enough band width, the optimization of energy resolution through a digital signal processing is possible.

A new energy reconstruction shaping filter leading to an improved energy resolution has been developed (Sect. 3), that is denoted as Zero Area Cusp (ZAC) filter. The Gerda experiment (Sect. 2), the readout of the data (Sect. 2.1) and the signal processing (Sect. 2.2) are described first. After the optimization of the ZAC filter (Sect. 4) the Phase I data have been reprocessed (Sect. 5).

2 The GERDA experiment

The design and the construction of Gerda were tailored to background minimization. The germanium detectors are mounted in low-mass ultra-pure copper holders and are directly inserted in 64 m$^3$ of liquid argon (LAr) acting as cooling medium and shield against external background radiation. The argon cryostat is complemented by a water tank with 5 m diameter which further shields from neutron and gamma backgrounds. It is instrumented with photomultipliers to veto the cosmic muons by detecting Čerenkov radiation. A further muon veto is provided by plastic scintillators installed on the top of the structure. A detailed description of the experimental setup is provided in Ref. [1].

A first physics data collection, denoted as Phase I, was carried out between November 2011 and June 2013. In Phase I eight p-type semi-coaxial detectors enriched in $^{76}$Ge from the Heidelberg–Moscow (HdM) [4] and IGEX [5] experiments and five Broad Energy Germanium (BEGe) detectors were used [6]. Three coaxial detectors with natural isotopic abundance from the Genius Test Facility (GTF) project [7, 8] were also installed. In a second physics run (Phase II) 30 BEGe detectors will be operated in addition to the eight semi-coaxial together with instrumentation to detect the LAr scintillation light to actively suppress background [9–11].

2.1 Signal readout and shaping with germanium detectors

Fig. 1

Typical readout scheme of a germanium detector with a charge sensitive preamplifier with open loop gain $A$. The detector with capacitance $C_D$ is operated with inverse bias voltage $HV$. The charge $Q_{in}$ is collected on the capacitor $C_f$ of $\sim$0.3 pF which then discharges because of the presence of the feedback resistor $R_f$=500 M$\Omega$

The typical readout of a germanium detector operated as a diode with inverse bias voltage applied consists of a charge sensitive preamplifier whose output wave form is either shaped and then processed by an analog to digital converter or, as in Gerda, directly digitized by a flash analog to digital converter (FADC). Figure 1 presents the detector and the charge sensitive preamplifier system consisting of a junction gate field-effect transistor (JFET) coupled to a feedback circuit. The capacitor $C_f$ integrates the charge from the detector causing a steep change in voltage at the preamplifier output. In order not to saturate the dynamic range of the preamplifier a feedback resistor $R_f$ is connected in parallel to the capacitor to bring back the voltage to its baseline value. The shape of the preamplifier output pulse is characterized by a fast step with a rise time of about 0.5–1.5 $\upmu$s corresponding to the charge collection process followed by an exponential tail. This tail with $\tau \sim$150 $\upmu$s is introduced by the discharge of the feedback capacitor (see Figs. 1, 3). In Gerda Phase I the recorded range amounts to 160 $\upmu$s with the rise of the pulse located in the center. A description of the Gerda readout scheme is given in Ref. [1].

Fig. 2

Signal and main noise sources in a germanium detector readout system. The trace recorded by the digitizer can be modeled as the output of a noiseless preamplifier, connected to a noiseless detector with capacitance $C_D$, a series voltage generator and a parallel current generator with spectral densities $s(f)$ and $p(f)$, respectively. $Q\cdot \delta (t)$ is the original current signal and $C_i$ is the preamplifier input capacitance

Figure 2 shows the signal and main intrinsic noise sources in the detector and preamplifier system. The intrinsic equivalent noise charge (ENC) for a given shaping time $\tau _s$ is given as:

$$\begin{aligned} ENC^2 = \alpha \frac{2kT}{g_m\tau _s}C_T^2 + \beta A_f C_T^2 + \gamma \left( e(I_G+I_L) + \frac{2kT}{R_f} \right) \tau _s \end{aligned}$$

(3)

where $g_m$ the JFET transconductance, $k$ is the Boltzmann constant, and $T$ the operating temperature. The constants $\alpha$, $\beta$ and $\gamma$ are of order 1 depending on the signal shaping filter (c.f. Ref. [12]). The series noise (first term) is proportional to the total capacitance $C_T$ which is the sum of the detector capacitance $C_D$, the feedback capacitance $C_f$ and the preamplifier input capacitance $C_i$. The second term represents the $1/f$ noise of the JFET with amplitude $A_f$ and is also proportional to the total capacitance. The third term is the parallel noise generated by the detector leakage current $I_L$, the gate current $I_G$ and the thermal noise of the feedback resistor $R_f$. The parallel noise is proportional to $\tau _s$ and the series noise to its inverse while the $1/f$ noise is independent of $\tau _s$. Therefore, the optimal shaping time is the one which minimizes the sum of the series and parallel noise. More detailed descriptions of the noise origin and its treatment in germanium detectors can be found in Refs. [12] and [13].

In Gerda Phase I an additional low-frequency disturbance comes from microphonics related to mechanical vibrations of the long wiring (30–60 cm) connecting the detectors to the preamplifiers.

2.1.1 Digital shaping

In Gerda Phase I the signals were digitized with 14 bits precision and 100 MHz sampling frequency [1]. 16384 samples were recorded per pulse (Fig. 3). After a $\sim$80 $\upmu$s long baseline the charge signal rises up with a $\sim$1 $\upmu$s rise time followed by a $\sim$80 $\upmu$s long exponential tail due to the discharge of the feedback capacitor.

The energy estimation was performed by applying a shaping filter to the digitized signal. The advantages with respect to analog shaping are that a large number of filters are available without restriction to the possible settings of the analog shaping module and that raw data remain available for further reprocessing.

Fig. 3

Typical wave form recorded in Gerda Phase I after baseline subtraction. A $\sim$80 $\upmu$s long baseline is recorded before each signal. The rise of $\sim$1 $\upmu$s is followed by an exponential decay tail of $\tau \sim$150 $\upmu$s due the discharge of the feedback capacitor

2.1.2 Energy resolution

The energy resolution of a germanium detector depends on the electronic noise, on the charge production in the crystal and on the charge collection properties of the diode and the shaping filter. A hypothetical $\gamma$ line at energy $E$ will have a $\Delta E$ (FWHM) expressed by:

$$\begin{aligned} \Delta E = 2.355\,\sqrt{\frac{\eta ^2}{e^2} ENC^2 + \eta F\cdot E + c^2\,E^2 } \end{aligned}$$

(4)

where:

• $\eta$ is the average energy necessary to generate an electron-hole pair ($\eta =2.96$ eV in Ge) and $F$ is the Fano factor ($\sim$0.1 for Ge [14]). This term contributes with about 1.8 keV at 2039 keV thus imposing a lower limit to the achievable $\Delta E$;

• $c$ is a parameter related to the quality of the charge collection and integration. An incomplete charge collection can be induced by charge recombination due to a too high impurity concentration or due to a too low bias voltage while a deficient integration of the collected charge can arise if a filter with a too short integration time is employed. The same effect is obtained in all cases resulting in low-energy tails of the spectral peaks. The parameter $c$ expresses therefore the amplitude of such tails. For the detectors used in Gerda Phase I, the third term of Eq. (4) is usually one order of magnitude lower than the electronic and charge production terms for events with energy up to 3 MeV.

If the charge collection inefficiency is not dominant, the optimization of the energy resolution depends almost exclusively on ENC, i.e. on the shaping filter. Given that ENC is independent of the energy, any $\gamma$ line with sufficiently high statistics can be exploited for the optimization of the shaping filter.

2.2 Data collection and processing in Gerda

Calibration data from the period November 2011–May 2013 were used to optimize the shaping filter. The detectors considered are ANG2–5 from the HdM experiment, RG1–2 from IGEX and four of the five BEGes (with names starting with “GD”). These are the same detectors used for the $0\nu \beta \beta$ decay analysis [2]. Since the electronic disturbances could change as a function of the detector configuration in Gerda, the calibration data were divided in four data sets as listed in Table 1. In total 72 (45) calibration measurements are available for the coaxial (BEGe) detectors.

Table 1 Definition of data sets. The run ranges and active detectors are listed

2.2.1 Calibration of the energy spectrum

Fig. 4

A $^{228}$Th calibration spectrum recorded by ANG5. The threshold is set to $\sim$400 keV

The calibrations were performed by inserting up to three $^{228}$Th sources in proximity of the detectors [15, 16]. The total activity of the sources was about 40 kBq at the beginning of Phase I. The duration of the measurements was between one and two hours. The energy threshold for the calibrations is $\sim$400 keV to reduce disk usage. At least ten peaks with energies between 0.5 and 2.6 MeV are visible in the recorded spectra (Fig. 4). While all peaks are exploited for the calibration of the energy scale, only the full energy peaks (FEP) are used in the fit of the FWHM as function of energy. This is necessary because the single escape peak (SEP), the double escape peak (DEP) and the 511.0 keV line are Doppler broadened.

Given the large number of calibration spectra to be analyzed, a fully automatized routine was developed and used throughout Phase I. The main steps of the procedure are:

• rejection of events which might decrease the precision of the calibration; e.g., coincidences between detectors, wave forms with superimposed events (pile-up events);

• search and identification of the peaks;

• fit of the peaks and automatic adjustment of the fitting function according to the number of events in the peak and the peak shape;

• extraction of the calibration curve;

• fit of the FWHM as a function of energy.

2.2.2 Signal processing

The signal processing of Gerda Phase I data was performed through an offline analysis of the digitized wave forms with the software tool Gelatio [17]. The standard energy reconstruction algorithm is a digital pseudo-Gaussian filter consisting of:

• a delayed differentiation of the sampled trace

  $$\begin{aligned} x_0[t] \rightarrow x_1[t] = x_0[t]-x_0[t-\delta ] \end{aligned}$$

  (5)

  where $x_0[t]$ is the signal height at time $t$ and $\delta$ was chosen to be 5 $\upmu$s;

• the iteration of 25 moving average (MA) operations:

  $$\begin{aligned} x_i[t] \rightarrow x_{i+1}[t] = \frac{1}{\delta }\sum _{t' = t - \delta }^t x_i[t'] \quad i=1,\ldots ,25 \end{aligned}$$

  (6)

The energy is given by the height of the output signal whose shape is close to a Gaussian.

This pseudo-Gaussian shaping is a high-pass filter followed by $n$ low-pass filters. The resolution obtained with the pseudo-Gaussian shaping is very close to optimal if the detectors are operated in conditions where the $1/f$ noise is negligible [12]. This is not the case for Gerda Phase I where the preamplifiers had to be placed at a distance of 30–60 cm from the crystals due to the low background requirements. The diodes and the pre-amplification chain were connected by OFHC copper strips insulated by soft teflon hoses. Hence, a significant low-frequency noise is present for some of the Gerda Phase I detectors.

As described in Sect. 2.1, the ENC depends on the properties of the detector, of the preamplifier and of the connection between them. In Gerda the diodes have different geometries and impurity concentrations resulting in different capacitances $C_D$ and different $I_L$. In addition, the non-standard connections between the detectors and the preamplifiers result in different input capacitances ($C_i$). It is therefore preferable to adapt the form and the parameters of the shaping filter to each detector separately.

3 ZAC: a novel filter for enhanced energy resolution

Several methods have been developed to obtain the optimum digital shaping for a given experimental setup [12, 13, 18, 19]. For series and parallel noise and with infinitely long wave forms it can be proven [18] that the optimum shaping filter for energy estimation of a $\delta$-like signal is an infinite cusp with the sides of the form $\exp {(t/\tau _s)}$ where $\tau _s$ is the reciprocal of the corner frequency; i.e., the frequency at which the contribution of the series and parallel noise of the referred input become equal. When dealing with wave forms of finite length, a modified cusp is obtained in which the two sides have the form of a sinh-curve. If low-frequency noise and disturbances are also present, the energy resolution is optimized using filters with total area equal to zero [20]. In addition, the low-frequency baseline fluctuations (e.g. due to microphonics) are well subtracted by filters with parabolic shape [21]. The best energy resolution for Gerda is achieved if a finite-length cusp-like filter with zero total area is employed. This can be obtained by subtracting two parabolas from the sides of the cusp filter keeping the area under the parabolas equal to that underlying the cusp.

In reality the detector output current is not a pure $\delta$-function, but has a width of approximately 1 $\upmu$s. If a cusp filter is used, this leads to the effect of a ballistic deficit [22, 23] and consequently to the presence of low-energy tails in the spectral peaks. This can be remedied by inserting a flat-top in the central part of the cusp with a width equal to almost the maximum length of the charge collection in the diode. The resulting filter is a Zero-Area finite-length Cusp filter with central flat-top that will be referred as ZAC from here on.

The ZAC filter was implemented as:

$$\begin{aligned} ZAC(t) =\nonumber \\ {\left\{ \begin{array}{ll} \sinh \left( \frac{t}{\tau _s} \right) + A\cdot \left[ \left( t-\frac{L}{2}\right) ^2 - \left( \frac{L}{2}\right) ^2 \right] \quad 0 < t < L\\ \sinh \left( \frac{L}{\tau _s} \right) \quad L < t < L + FT \\ \sinh \left( \frac{2L+FT-t}{\tau _s} \right) + A\cdot \left[ \left( \frac{3}{2}L+FT-t\right) ^2 -\left( \frac{L}{2}\right) ^2 \right] \quad L+FT < t < 2L+FT \end{array}\right. } \end{aligned}$$

(7)

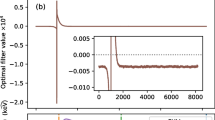
where $\tau _s$ is the equivalent of the shaping time for an analog shaping filter, $2L$ is the length of the cusp filter and $FT$ is that of the flat-top and where the constant $A$ is chosen such that the total integral is zero. The numerical expression of the ZAC filter is obtained through the substitution $t\rightarrow \Delta t\cdot i$ where $\Delta t$ is the sampling time and $i$ the sample index; the maximum number of samples in the ZAC filter is $n_{ZAC}$. A graphical representation of the ZAC filter construction is provided in Fig. 5.

Fig. 5

Amplitude versus time for the ZAC filter (red full line). It is composed of the finite-length cusp (blue dashed) from which two parabolas are subtracted on the cusp sides (green dash-dotted)

Before proceeding with the shaping the original current pulse has to be reconstructed from the preamplifier output wave form (Fig. 3). This is performed via a deconvolution of the preamplifier response function, an exponential curve with decay time $\tau =R_fC_f$. Specifically, it is implemented as the convolution with the filter consisting of two elements, $f_{\tau }=[1,-\exp {(-\frac{\Delta t}{\tau })}]$. No correction for the finite band width of the electronics was implemented. Since the convolution operation is commutative, the convolution between the ZAC filter and the inverse preamplifier response function $f_{\tau }$ can be performed once for all:

$$\begin{aligned} \nonumber FF[i]= & {} ZAC[i] \cdot \left( -e^{-\frac{\Delta t}{\tau }}\right) + ZAC[i+1] \cdot 1\nonumber \\&\quad i=1,\ldots ,n_{ZAC}-1 \end{aligned}$$

(8)

The final filter ($FF$) obtained is shown in red in Fig. 6. A convolution of each individual signal trace $x$ with $FF$ is then performed:

$$\begin{aligned} y[i] = \sum _{k=i}^{i+n_{ZAC}-2} x[k] \cdot FF[i+n_{ZAC}-1-k] \nonumber \\ \quad i=1,\ldots ,n_x-n_{ZAC}+2 \end{aligned}$$

(9)

$n_x$ is the number of samples in the trace. Typically $n_x$ is set to 16384 and $n_{ZAC}$ ranges from 16060 to 16120. The output $y$ for the trace of Fig. 3 is shown as blue full line in Fig. 6. The energy $E$ is then estimated as the maximum of this convoluted signal $y$.

4 Optimization of the ZAC filter on calibration data

The optimization of the ZAC filter using the Phase I calibration data was performed separately for each detector. The first and the last calibration run of each period were selected (Table 1). Given their longer duration one more run taken in the middle of the period was used for data sets A and D as well. It is expected that no change was present in the electronic noise within the same data set. In this case the filter parameters giving the best energy resolution should be the constant for each data set.

Fig. 6

The ZAC filter after the convolution with the inverse preamplifier response function (red dashed) and the wave form of Fig. 3 after the convolution with it (full blue)

The filter optimization was performed on the FEP of $^{208}$Tl, i.e. the 2614.5 keV line. Quality cuts were applied prior to the energy reconstruction that was performed only on the surviving events. The energy spectrum was reconstructed with different values of the four filter parameters $L$, $FT$, $\tau _s$ and $\tau$. In particular:

• the total filter length $2L+FT$ was varied for only one calibration run between 120 and 163 $\upmu$s. As expected [18] the best energy resolution was obtained for the longest possible filter. Given the variability of the trigger time within a 2 $\upmu$s range the maximum of the shaped filter can be at one of the extremes of the wave form when the maximum filter length of 163 $\upmu$s is used leading to a wrong energy estimation. This effect completely disappears if the filter is shortened by 2 $\upmu$s. Hence, the optimization was performed with $\sim$161 $\upmu$s long filters;

• the optimal length of $FT$ is related to the charge collection time in the detector. For coaxial detectors this is typically between 0.6 and 1 $\upmu$s depending on the electric field configuration in the detector and on the location of the energy deposition. For BEGes it is slightly longer due to the slower charge drift. The value of $FT$ was therefore varied between $0.5$ and 1.5 $\upmu$s in 120 ns steps;

• the optimal filter shaping time $\tau _s$ depends on the electronic noise spectrum as described in Sect. 2.1. Typically, $\tau _s$ is of order of 10 $\upmu$s. The optimization was therefore performed with values of $\tau _s$ between 3 and 30 $\upmu$s in steps of 1 $\upmu$s. Since the optimal $\tau _s$ was not infinite, the noise present in Phase I data had a non negligible parallel component;

• the value of $\tau$ can in principle be calculated knowing the feedback resistance and capacitance. In reality $\tau$ is modified by the presence of parasitic capacitance in the front-end electronics. Moreover, given the presence of long cables a signal deformation can arise. Therefore, $\tau$ is normally estimated by fitting the pulse decay tail. This was not possible due to the presence of more than one exponential. Therefore $\tau$ was varied between 100 and 300 $\upmu$s with 5 $\upmu$s step size.

Table 2 Optimized parameters of the ZAC filter for period D. While the filter length $2L$ is equal for all the detectors $FT$ varies between 0.6 and 1.2 $\upmu$s according to the charge collection properties of each diode

The peak at 2614.5 keV was fitted with the function [24] for each combination of the filter parameters:

$$\begin{aligned} f(E)= & {} A\exp {\left( -\frac{(E-\mu )^2}{2\sigma ^2} \right) } + B + \frac{C}{2} \text{ erfc } \left( \frac{E-\mu }{\sqrt{2}\cdot \sigma } \right) \nonumber \\&\quad +\,\frac{D}{2} \exp {\left( \frac{E-\mu }{\delta } \right) } \text{ erfc } \left( \frac{E-\mu }{\sqrt{2}\cdot \sigma } + \frac{\sigma }{\sqrt{2}\cdot \delta } \right) \end{aligned}$$

(10)

corresponding to a Gaussian peak with a low-energy tail (last term) sitting on flat background and on a step-like function (third term) which describes the continuum on the left side of the peak. The FWHM was obtained from the fitting function after the subtraction of the flat and step-like background components. The energy resolutions resulting from different parameters of the ZAC filter were compared and the parameters leading to a minimal FWHM were chosen for the full reprocessing of the data. For the detectors of the $0\nu \beta \beta$ analysis the optimal parameters of the ZAC filter for period D are reported in Table 2 as an example.

5 Results

The parameter optimization for the ZAC filter provided results in agreement with expectations: for each detector the optimal filter parameters are stable within the same data set, but they can vary for those detectors that changed configuration in time. This confirms the dependence of the microphonic disturbances on the cable routing. Hence, all Phase I calibration and physics data were reprocessed with the optimal parameters of the ZAC filter.

Fig. 7

$^{208}$Tl FEP data for ANG5 at 2614.5 keV. The curves and parameter values corresponding to the best fit for the ZAC and the pseudo-Gaussian shaping are shown

Table 3 Average FWHM over the complete Phase I period. The improvement is computed as the difference between the FWHM for the pseudo-Gaussian and that for the ZAC filter. Only the statistical uncertainty due to the peak fit is quoted

Fig. 8

$^{208}$Tl FEP data for GD35B at 2614.5 keV. The curves and parameter values corresponding to the best fit for the ZAC and the pseudo-Gaussian shaping are shown

A first remarkable result is the improvement of the energy resolution between 5 and 23 % for the $^{208}$Tl FEP at 2614.5 keV of all the Phase I data. As an example Figs. 7 and 8 show the summed spectrum of all Phase I calibrations around the 2614.5 keV line for ANG5 and GD35B, respectively. In both cases, the amplitude of the Gaussian component is larger for the spectrum obtained with the optimized ZAC filter and its width is correspondingly reduced. The parameters $B$ and $C$ describing the continuum below the peak are compatible for the two shaping filters.

Fig. 9

Resolution curve (Eq. 4 with $w_p^2=2.355^2\eta F$) for ANG5 calculated for all Phase I calibration spectra merged together for pseudo-Gaussian (full line) and ZAC (dashed line) shaping

Fig. 10

FWHM of the full energy peak of $^{208}$Tl at 2614.5 keV for ANG2

Fig. 11

FWHM of the full energy peak of $^{208}$Tl at 2614.5 keV for GD35B. The error bars are partially within the symbols size

While for the coaxial ANG5 a low-energy tail has to be accounted for in the fit (Fig. 7) the amplitude of the tail in the BEGe GD35B is negligible. The tail it therefore automatically removed from the fit (Fig. 8). This is attributed to the smaller dimensions of the BEGe detector and its reduced charge collection inefficiency. In case of ANG5 the tail amplitude $D$ is strongly reduced when the ZAC shaping is used thanks to the presence of the flat-top that allows for an improved integration of the collected charge.

A deeper understanding of the result is provided by studying the evolution of the FWHM as function of energy which is fitted according to Eq. (4). An example is given in Fig. 9 showing the resolution curve of all calibration runs for ANG5. As expected the major improvement regards the ENC which reduces FWHM$^2$ at all energies by a constant. For both, the pseudo-Gaussian and the ZAC filter, the charge production term $w_p^2=2.355^2\eta F$ is compatible with the theoretical value of $1.64\cdot 10^{-3}$ keV. Finally, the charge collection term $c^2$ for the ZAC filter is compatible within the uncertainty with the value obtained for the pseudo-Gaussian filter. The large uncertainty of this parameter is due to the lack of peaks above 3 MeV which makes the fit imprecise. This term is the smallest of the three and accounts for maximally 15 % of the width at 2614.5 keV. A consistent behavior is observed for the other detectors as well.

One of the original motivations for the application of the ZAC filter to the Gerda Phase I data was the observation of temporary deterioration of the energy resolution in some detectors interpreted as due to time-evolving microphonic disturbance not being properly treated by the pseudo-Gaussian filter. This is confirmed by the comparison of the FWHM over time for both filters as shown for ANG2 and GD35B in Figs. 10 and 11, respectively. In case of ANG2 the FWHM at 2614.5 keV obtained with the pseudo-Gaussian shaping fluctuates between 4.5 and 4.9 keV. In June 2012 stronger microphonic disturbance caused a FWHM increase up to about 5.1 keV. When using the ZAC filter the effect is significantly reduced and the FWHM obtained for the affected calibrations is brought back to a value consistent with the average. Stronger fluctuations were present for GD35B. A very poor energy resolution was observed during the first month of operation together with a continuous worsening of the spectroscopic performances in the last 4 months of Phase I. Also in this case the ZAC filter energy estimate is unaffected by the low-frequency baseline fluctuations induced by microphonics and allowed to stabilize the FWHM over time to about 2.8 keV (at 2614.5 keV).

Fig. 12

$^{42}$K peak for the coaxial detectors in the energy spectrum for all Phase I physics runs. The curves and parameter values relative to the best fit for the ZAC and the pseudo-Gaussian shaping are reported

The Phase I average FWHM for the $^{208}$Tl line at 2614.5 keV for each detector obtained with the pseudo-Gaussian and the ZAC filter are reported in Table 3. The average improvement was calculated as the difference between the two values. This is about 0.31 keV for the coaxial and 0.13 keV for the BEGe detectors apart from GD35B for which a much larger improvement is obtained as described above.

The comparison of the effective energy resolution achieved with Phase I physics data can be performed exclusively on the $^{42}$K peak at 1524.6 keV which is the only background line with a sufficient number of counts for a spectral fit. The summed energy spectra in the 1515–1535 keV range for all Phase I data for the six coaxial and the four BEGe detectors used for the $0\nu \beta \beta$ decay analysis are shown in Figs. 12 and 13, respectively. The FWHM obtained for the pseudo-Gaussian shaping and the coaxial detectors is $4.49\pm 0.11$ keV. This is 0.30 keV larger than the value expected from the calibration data. The reason is given by drifts of the electronics between calibrations and microphonics mainly present in ANG2 and ANG4. For the ZAC filter the drifts between different physics runs are reduced because the microphonics and the noise are treated better. The resulting FWHM of the $^{42}$K peak is $4.09\pm 0.11$ keV and is only $0.15$ keV higher than expected from calibration data. The net improvement in energy resolution at 1524.6 keV for the coaxial data is 0.40 keV. In case of BEGes the ZAC shaping provides a $2.75\pm 0.21$ keV FWHM compared to $3.05\pm 0.30$ keV obtained with the pseudo-Gaussian. The comparison in this case is harder due to the very limited number of events. The improvement on the FWHM of the $^{42}$K line is in agreement with the expectation from the calibration data.

Fig. 13

$^{42}$K peak for the BEGe detectors in the energy spectrum for all Phase I physics runs. The curves and parameter values relative to the best fit for the ZAC and the pseudo-Gaussian shaping are reported

The improvement in energy resolution given by the ZAC filter is also reflected in a more precise estimation of the energy scale for the single calibration runs. In Gerda a second degree polynomial is used as a calibration curve in order to account for the preamplifier non-linearity. Figs. 14 and 15 show the residuals of the $^{228}$Th peak positions from the corresponding calibration curve averaged over all Phase I calibration runs. Both for the Gaussian and the ZAC shaping, the average residuals are of order of $10^{-2}$ keV. Hence, they are much smaller than the peak widths.

Fig. 14

Average residuals of the $^{228}$Th peak positions relative to literature values for ANG5. The error bars on the data points correspond to the RMS of the residuals for a given peak

Fig. 15

Average residuals of the $^{228}$Th peak positions relative to literature values for GD35B. The error bars on the data points correspond to the RMS of the residuals for a given peak

A more informative estimation of the energy calibration precision is obtained by calculating the uncertainty $\delta _{E}$ of the calibration curve at a given energy, e.g. at 1524.6 keV. For each calibration run the quantity $\delta _{E}(E=1524.6$ keV) is calculated by error propagation on the calibration curve parameters. Using Monte Carlo (MC) simulations $10^5$ events were randomly generated according to a Gaussian distribution with zero mean and $\delta _{E}(E=1524.6$ keV). The distributions from all Phase I calibration runs are then summed up and the systematic uncertainty of the energy scale at 1524.6 keV is given by the half-width of the 68 % central interval. This results to be between 0.03 and 0.07 keV and is up to $16\,\%$ smaller for ZAC shaping with respect to the pseudo-Gaussian filter.

A cross check of the reprocessed data is given by the event-by-event comparison of the energy obtained with the ZAC and the pseudo-Gaussian filter. This is performed by calculating the energy difference of the events in the 2614.5 keV peak as shown in Fig. 16 for ANG2 during a typical calibration run. For all the detectors this distribution is a Gaussian with a mean value compatible with zero and a width $\sigma \sim 0.8$ keV. The same behavior is observed at all energies for both calibration and physics data.

Fig. 16

Distribution of the difference between the energy estimated with the pseudo-Gaussian and that obtained with the ZAC filter for the $^{208}$Tl FEP events at 2614.5 keV. The data refer to a standard calibration and are for ANG2

6 Summary

The presence of low-frequency noise in the signals of Gerda Phase I mostly induced by microphonic disturbance leads to a degraded energy resolution for some of the deployed detectors. Spectroscopic performance close to optimal is obtained by the use of the ZAC shaping filter. This novel Zero Area Cusp filter is obtained by subtracting two parabolas from the sides of the cusp filter keeping the area under the parabolas equal to that underlying the cusp. A selection of calibration runs has been exploited for the optimization of the ZAC filter. All calibration data sets have then been reprocessed using the optimal filter parameters. An average improvement of 0.30 keV in FWHM has been obtained for both coaxial and BEGe detectors. In one case (GD35B) the energy resolution is improved by 0.86 keV with the excellent low-frequency rejection provided by the ZAC filter.

The stability of the filter parameters over time for the same detector configuration in Gerda along with its outstanding low-frequency noise rejection capabilities provides a FWHM improvement of 0.40 (0.30) keV at the $^{42}$K line in the Phase I physics data for the coaxial (BEGe) detectors. Any improvement in the energy resolution will increase the sensitivity of the experiment and allow a better understanding of the experimental background.

The Phase I physics data, reprocessed with the ZAC shaping, will be combined with the Phase II data in a future analysis of the $0\nu \beta \beta$ decay. The optimization of the shaping filter will be performed from the beginning of Phase II following a procedure similar to the one described in the present work.