Introduction

The numerical solution of boundary value problems is of great importance as a result of its wide application in scientific and technological research [1]. Many researchers have developed various numerical methods, especially iterative methods to approximate different types of differential equations, see [2–5]. In recent years, there has been a growing interest in the treatment of iterative approximation such as variational iteration method, fixed point iteration and so on [6], variational iteration method has been used over the years to obtain an approximate solution of some boundary value problems, see [7, 8]. On the other hand, fixed point iteration is a method of computing fixed point of iterated function, it is a well-known method of approximation whose version is the variation iteration method, see [9, 10]. Obviously, these methods have been proved by many researchers to be powerful tools in solving boundary value problems [11]. However, there are noticeable shortcomings in implementations of these methods especially the use of arbitrary function as a starting value, an in-appropriate choice of starting function may affect the rate of convergence, see [11, 12].

In this paper, the propose method is an elegant combination of variational iteration method and fixed point iteration method with the use of finite element method to determine the starting function.

Analysis of variational-fixed point iterative scheme

The variational-fixed point iteration is the combination and application of variational iteration method and fixed point iterative process endowed with finite element method.

To illustrate the basic technique of variational iteration method, we consider the following general differential equation

$$\begin{aligned} Lu + Nu =g(x) \end{aligned}$$
(1)

where L is linear operator, N is nonlinear operator and g(x) is forcing term. According to variational iteration method, see [13, 14], a correctional functional of (1) can be constructed as follows

$$\begin{aligned} u_{n+1}(x) = u_{n}(x) + \int _{0}^{x}\lambda (Lu_{n}(s) + Nu_{n}(s)-g(s)) \mathrm{{d}}s \end{aligned}$$
(2)

where \(\lambda\) is the Lagrange multiplier [15, 16] which can be determined by variational theory, thus

$$\begin{aligned} \delta u_{n+1}(x)=\; & {} \delta u_{n}(x) + \delta \int _{0}^{x} \lambda (Lu_{n}(s) + Nu_{n}(s)-g(s))\mathrm{{d}}s\\ \delta u_{n+1}(x)= \;& {} \delta u_{n}(x) + \int _{0}^{x}\delta {\lambda (Lu_{n}(s)}\mathrm{{d}}s \end{aligned}$$

its stationary conditions can be obtained using integration by parts. The second term in the right is called correction and \(\tilde{u}u_{n}\) is considered as a restricted variation, i.e \(\delta u_{n}=0\). Thus, the Lagrange’s multiplier [17, 19] can be identified as

$$\begin{aligned} \lambda (x) = (-1)^{n}(s-x)^{n-1}/(n-1)!. \end{aligned}$$

The given solution is considered as the fixed point of the following functional [11] under the suitable choice of initial approximation [21] \(u_{0}(x)\) at \(n=0\). We use finite element method to determine the starting function to avoid the arbitrary choice of starting function. After single iteration process we obtained \(u_{1}\); repeating the process iteratively the term to be integrated become larger and cumbersome to operate and the result of each iteration step diverges from exact solution. Based on this fact we introduce the application of fixed point iterative process to overcome it. Thus we have the following theorem:

Theorem 1

Let (E, d) be a complete metric space and T be a self map on E. Further, let \(y_{o} \in E\) and let \(y_{n+1}=f(T,y_{n})\) denotes an iteration procedure which gives a sequence \(\{y_{n}\}\) . Then T is an iteration process and defined for arbitrary \(y_{0}\) by

$$\begin{aligned} y_{n+1}=f(T,y_{n})=(1-\alpha _{n})y_{n}+\alpha _{n} Ty_{n},\quad n\ge 0 \end{aligned}$$
(3)

where \(\{a_{n}\}\) is a real sequence satisfying \(\alpha _{n}=1,\) \(0 \le \alpha _{n} \le 1\) for \(n \ge 0\) and \({\sum \nolimits _{n=0}^{\infty } \alpha _{n} = \infty }.\)

Proof

Let

$$\begin{aligned} y^{(iv)}+p(x)y^{\prime \prime \prime }+q(x)y^{\prime \prime }+r(x)y^{\prime }+s(x)y=t(x) \end{aligned}$$

such that

$$\begin{aligned} y(a)=y(b)=y^{\prime \prime }(b)=y^{\prime \prime }(\alpha )=0, \quad a \le \alpha \le b; \end{aligned}$$

where \(p,q,r,s,f\in C[a,b]\), then the scheme

$$\begin{aligned} y_{n+1}^{(iv)}=(1-\lambda _{n})y_{n}^{(iv)}+ \lambda _{n}(1-\alpha )y_{n}^{(iv)} \end{aligned}$$
(4)

obtained by harnessing Mann and Banach fixed point iteration [6, 20], to yield

$$\begin{aligned} y_{n+1}^{(iv)}= \lambda (t(x)-p(x)y_{n}^{\prime \prime \prime }-q(x)y_{n}^{\prime \prime }-r(x)y_{n}^{\prime }- s(x))y_{n} + (1-\lambda )y_{n}^{(iv)} \end{aligned}$$
(5)

and converges for \(0\le \lambda _{n}\le 1\). Now let

$$\begin{aligned} y^{(iv)}= f(x,y,y^{\prime },y^{\prime \prime },y^{\prime \prime \prime }). \end{aligned}$$
(6)

Therefore, for any y(x) solution of the integral equation on [a, b]

$$\begin{aligned} y(x)= \int _{a}^{b}(G(x,s)f(t,y(t),y^{\prime }(t),y^{\prime \prime }(t),y^{\prime \prime \prime }(t))\mathrm{{d}}t + v(x) \end{aligned}$$
(7)

where G(x, t) is a green function of the associated boundary value problem and v(x) is a solution of \(y^{(iv)}=0\) that satisfies boundary conditions. Now if we let \(T:C^{1}[a,b]\rightarrow C^{1}[a,b]\) be defined by

$$\begin{aligned} (Ty)(x)= \int _{a}^{b}(G(x,s)f(t,y(t),y^{\prime }(t),y^{\prime \prime }(t),y^{\prime \prime \prime }(t))\mathrm{{d}}t + v(x) \end{aligned}$$
(8)

then T is an operator such that any y(x) is a solution of (6) at fixed point of T and can be referred as a fixed point operator. For convergence of (3) and (5) we let

$$\begin{aligned} y_{n+1}=\; & {} (1-\alpha _{n})y_{n}+\alpha _{n} Ty_{n} \\ y_{n+1}^{\prime }=\; & {} (1-\alpha _{n})y_{n}^{\prime }+\alpha _{n} Ty_{n}^{\prime } \\ y_{n+1}^{\prime \prime }=\; & {} (1-\alpha _{n})y_{n}^{\prime \prime }+\alpha _{n} Ty_{n}^{\prime \prime }\\ y_{n+1}^{\prime \prime \prime }=\; & {} (1-\alpha _{n})y_{n}^{\prime \prime \prime }+\alpha _{n} Ty_{n}^{\prime \prime \prime } \end{aligned}$$
$$\begin{aligned} y_{n+1}^{(iv)}=\; & {} (1-\alpha _{n})y_{n}^{(iv)}+\alpha _{n} Ty_{n}^{(iv)}. \end{aligned}$$
(9)

From Eq. (8) it follows that

$$\begin{aligned} (Ty_{n})^{\prime }(x)= \;& {} \int _{x_{1}}^{x_{2}}\delta /\delta x(G(x,s)f(t,y(t),y^{\prime }(t),y^{\prime \prime }(t),y^{\prime \prime \prime }(t))\mathrm{{d}}t + v(x)^{\prime }\\ (Ty_{n})^{\prime \prime }(x)=\; & {} \int _{x_{1}}^{x_{2}}\delta ^{2}/\delta x^{2}(G(x,s)f(t,y(t),y^{\prime }(t),y^{\prime \prime }(t),y^{\prime \prime \prime }(t))\mathrm{{d}}t + v(x)^{\prime \prime }\\ (Ty_{n})^{\prime \prime \prime }(x)=\;& {} \int _{x_{1}}^{x_{2}}\delta ^{3}/\delta x^{3}(G(x,s)f(t,y(t),y^{\prime }(t),y^{\prime \prime }(t),y^{\prime \prime \prime }(t))\mathrm{{d}}t + v(x)^{\prime \prime \prime }\\ \end{aligned}$$
$$\begin{aligned} (Ty_{n})^{(iv)}(x)= & {} \int _{x_{1}}^{x_{2}}\delta ^{4}/\delta x^{4}(G(x,s)f(t,y(t),y^{\prime }(t),y^{\prime \prime }(t),y^{\prime \prime \prime }(t))\mathrm{{d}}t + v(x)^{(iv)}. \end{aligned}$$
(10)

Therefore Eqs. (9) and 10 become

$$\begin{aligned} y_{n+1}^{(iv)}=(1-\alpha _{n})y_{n}^{(iv)}+\alpha _{n}\int _{x_{1}}^{x_{2}}\delta ^{4}/\delta x^{4}(G(x,s)f(t,y(t),y^{\prime }(t),y^{\prime \prime }(t),y^{\prime \prime \prime }(t))\mathrm{{d}}t + v(x)^{(iv)}. \end{aligned}$$
(11)

Also, combining Eqs. (7) and (11) yields

$$\begin{aligned} y_{n+1}^{(iv)}=(1-\alpha _{n})y_{n}^{(iv)}+\alpha _{n} Ty_{n}^{(iv)}. \end{aligned}$$
(12)

Therefore scheme (3) and (5) are convergent. This scheme is use to approximate boundary value problems iteratively with the use of arbitrary initial approximation \(y_{0}\) at \(n=0\). Since the variational iteration method and fixed point iteration methods are similar [10]. We let \(y_{0}=u_{1}\) to avoid the assumption of the arbitrary function \(y_{0}\) where the process will be carried out iteratively until convergence is obtained or the iteration is terminated. However, the finite element methods are the Galerkin method, collocation method, Raleigh-Ritz method, etc. Galerkin method is an approximate solution of boundary value problems suggested by Galerkin [18], based on the requirement that the basis function \(\phi _{0},\phi _{1},\phi _{2},\ldots ,\phi _{n}\) be orthogonal to the residual

$$\begin{aligned} \int \psi (x_{i},a_{0},a_{1},\ldots ,a_{n})\phi _{i}\mathrm{{d}}x=0 \end{aligned}$$

\(i=0,1,2,3,\ldots ,n\). This gives rise to the following system of linear algebraic equations for the coefficients of the approximation solution

$$\begin{aligned} y_{n}(x)=\phi _{0}(x)+a_{1}\phi _{1}(x)+a_{2}\phi _{2}(x)+\cdots +a_{n}\phi _{n}(x) \end{aligned}$$

of the boundary value problem

$$\begin{aligned} Ly=y^{(iv)}+p(x)y^{\prime \prime \prime }+q(x)y^{\prime \prime }+r(x)y^{\prime }+s(x)y=f(x),\quad 0 \le x \le 1 \end{aligned}$$

such that

$$\begin{aligned} y(0)=y(0)=y^{\prime \prime }(1)=y^{\prime \prime }(\alpha )=0, \quad 0 \le \alpha \le 1. \end{aligned}$$

Therefore,

$$\begin{aligned} a_{1}L(\phi _{1},\phi _{1})+a_{2}L\phi _{1},\phi _{2}+\cdots +a_{n}L\phi _{n},\phi _{1}= \;& {} (f-L(\phi _{0},\phi _{1}))\\ a_{1}L(\phi _{1},\phi _{2})+a_{2}L\phi _{2},\phi _{2}+\cdots +a_{n}L\phi _{n},\phi _{2}= \;& {} (f-L(\phi _{0},\phi _{2}))\\&\vdots&\\ a_{1}L(\phi _{1},\phi _{n})+a_{2}L\phi _{2},\phi _{n}+\cdots +a_{n}L\phi _{n},\phi _{n}=\; & {} (f-L(\phi _{0},\phi _{n})). \end{aligned}$$

The weight functions are taken with the concept of inner product and orthogonality, it is obvious that the inner product of the two function in a certain domain is

$$\begin{aligned} \left\langle f,g \right\rangle =\int _{a}^{b} f(x)g(x)\mathrm{{d}}x=0 \end{aligned}$$

which is used to determine the starting function of the variational iteration method instead of an arbitrary choice. \(\square\)

Numerical examples

In this section, two experiments are considered to demonstrate present methods:

Example 1

Consider

$$\begin{aligned} y^{(iv)}-y^{\prime \prime }=-2, \quad 0\le x\le 1 \end{aligned}$$
(13)

subject to the boundary conditions

$$\begin{aligned} y(0)=y^{\prime \prime }(1/2)=y^{\prime \prime \prime }(0)=0, \quad y(1)=1. \end{aligned}$$

The following must be observed: Galerkin method of approximation is used to determine the initial approximation of variational iteration method whose trial function

$$\begin{aligned} U(x)=U_{0}(x) + \sum _{i=1}^{n}C_{i}U_{i}(x) \end{aligned}$$

is called the basis function, the approximate solution we sought. Where \(U_{0}(x)=x, U_{1}=(x-x^{4}), U_{2}=(x-x^{5})\)

$$\begin{aligned} U(x)= x + C_{1}(x-x^{4}) + C_{2}(x-x^{5}). \end{aligned}$$
(14)

We differentiate the Eq. (14) successively to obtain second and fourth derivatives and then substitute in Eq. (13) to get the residual

$$\begin{aligned} R(x,C_{1},C_{2})=-24C_{1} -120C_{2}x +12C_{1}x^{2} + 20C_{2}x^{3} + 2. \end{aligned}$$
(15)

A weight function is chosen within the bases function with the concepts of inner product and orthogonality

$$\begin{aligned} \left\langle U,R \right\rangle = \int _{a}^{b}U_{i}(x){D[U_{0}(X)+ \sum _{i=1}^{n}C_{i}U_{i}(x)]}\mathrm{{d}}x=0. \end{aligned}$$

These are sets of n-order linear equations which is solved to obtain all C i coefficients as follows:

$$\begin{aligned} \int _{0}^{1}(x-x^{4})(-24C_{1} -120C_{2}x +12C_{1}x^{2} + 20C_{2}x^{3} + 2)\mathrm{{d}}x=0 \end{aligned}$$

we obtain

$$\begin{aligned} -37/2 C_{2} - 207/35 C_{1} = -3/5. \end{aligned}$$
(16)

Also

$$\begin{aligned} \int _{0}^{1}(x-x^{5})(-24C_{1} -120C_{2}x +12C_{1}x^{2} + 20C_{2}x^{3} + 2)\mathrm{{d}}x=0 \end{aligned}$$

we get

$$\begin{aligned} -132/63 C_{2} - 13/2 C_{1} = -2/3 \end{aligned}$$
(17)

solving these Eqs. (16) and (17) simultaneously we obtain \(C_{}=308/4331, C_{2}=42/4331\). We substitute these constants in (14), hence the approximation solution we sought for.

$$\begin{aligned} U(x)= x + 308/4331(x-x^{4}) + 42/4331(x-x^{5}). \end{aligned}$$
(18)

The second step is the use variational iteration method to determine the starting function of the fixed point iterative procedure; we construct the correct functional of (13) as follows:

$$\begin{aligned} t_{n+1}(x) = t_{n}(x) + \int _{0}^{x}\lambda (t^{(4)}_{n}(s) - t^{(2)}_{n}(s)-g(s)) \mathrm{{d}}s \end{aligned}$$

at \(n=0\)

$$\begin{aligned} t_{1}(x) = t_{0}(x) + \int _{0}^{x}\lambda (t^{(4)}_{0}(s) - t^{(2)}_{0}(s)-g(s)) \mathrm{{d}}s. \end{aligned}$$
(19)

We let

$$\begin{aligned} t_{0}(x)= U(x)= x + 308/4331(x-x^{4}) + 42/4331(x-x^{5}) \end{aligned}$$
(20)

we differentiate (20), i.e \(t_{0}(x)\) successively to obtain its second and fourth derivative and substitute same in Eq. (19) to have

$$\begin{aligned} t_{1}(x)&= x + 308/4331(x-x^{4}) + 42/4331(x-x^{5}) \nonumber \\&\quad +\int _{0}^{x}(s-x^{3})/25986 (-7392x-5040x+3696x^{2}-840x^{3}+2)\mathrm{{d}}s \end{aligned}$$
$$\begin{aligned} t_{1}(x)&= 1/4331(4681x - 308x^{4} - 42x^{5}) + 1/1732 (635x^{4}/3-840x^{5}+616x^{6}+140x^{7})\nonumber \\&\quad -1/51972(1270x^{4}-5040x^{5}+3696x^{6}+840x^{7}). \end{aligned}$$
(21)

When the process is repeated for further iterations, the function to be integrated is getting larger and complex, where iterated values diverge from the analytical solution. Based on this fact, We let \(y_{0}=U_{1}(x)\), where \(U_{1}(x)\) is the iterative function obtained after single iteration taken as an initial values for fixed point iterative technique. The scheme in (12) the fixed point iterative procedure can be used as follows

$$\begin{aligned} y_{n+1}^{(iv)}(x)=y_{n}^{\prime \prime }(x)-2 \end{aligned}$$
(22)

at \(n=0\)

$$\begin{aligned} y_{1}^{(iv)}(x)=y_{0}^{\prime \prime }(x)-2. \end{aligned}$$
(23)

But

$$\begin{aligned} y_{0}(x)&=t_{1}(x) = 1/4331(4681x - 308x^{4} - 42x^{5}) + 1/1732 (635x^{4}/3-840x^{5}+616x^{6}+140x^{7}) \nonumber \\&\quad -1/51972(1270x^{4}-5040x^{5}+3696x^{6}+840x^{7}). \end{aligned}$$
(24)

We differentiate the Eq. (24) twice to get \(y_{0}^{\prime \prime }\) and then substituted it into the given Eq. (23) to obtain

$$\begin{aligned} y_{1}^{(iv)}(x)=-1.29324819x^{2}+1.939505888x^{3}-3.057954283x^{4}-0.4040637266x^{5}-2. \end{aligned}$$
(25)

To obtain \(y_{1}(x)\), we integrate (25) four times successively and imposing the boundary conditions to get

$$\begin{aligned} y_{1}(x)&=-35x^{9}/311832-11x^{8}/17324+4x^{7}-x^{6}/360-x^{4}/12-0.1273074324x^{2}\\&\quad +0.9586273016x. \end{aligned}$$

The repeat the process at \(n=2,3 \ldots\) until the iteration is terminated or it converges with the analytical solution, after few iterations we get

$$\begin{aligned} y_{5}(x)&=0.9632277022x+0.1131826518x^{2}-0.0739028367x^{4}\\&\quad -0.002462970407x^{6}-0.00004406199500x^{8}-4.8098132 \times 10^{-7}x^{10}\\&\quad -4.175351396 \times 10^{-9}x^{12}-1.223616824 \times 10^{-12}x^{16}\\&\quad -1.145095958 \times 10^{-13}x^{17}+3.559612579 \times 10^{-12}x^{15}\\&\quad -2.294149120 \times 10^{-11}x^{14}\nonumber . \end{aligned}$$

Example 2

Consider

$$\begin{aligned} y^{(iv)}-y^{\prime \prime }=-12x^{2}, \quad 0\le x\le 1 \end{aligned}$$
(26)

subject to the boundary conditions

$$\begin{aligned} y(0)=y^{\prime \prime }(0)=y^{\prime \prime \prime }(1/2)=0,\quad y(1)=13. \end{aligned}$$

We let

$$\begin{aligned} U(x)=U_{0}(x) + \sum _{i=1}^{n}C_{i}U_{i}(x) \end{aligned}$$

which is the basis function where \(U_{0}(x)=13x, U_{1}=(x-x^{4}), U_{2}=(x-x^{5})\)

$$\begin{aligned} U(x)=13x + C_{1}(x-x^{4}) + C_{2}(x-x^{5}). \end{aligned}$$
(27)

We differentiate Eq. (27) successively to obtain second and fourth derivatives and then substitute same in (26) the given differential equation to get the residual

$$\begin{aligned} R(x,C_{1},C_{2})=-24C_{1} -120C_{2}x +12C_{1}x^{2} + 20C_{2}x^{3} + 12x^{2}. \end{aligned}$$
(28)

A weight function are chosen within the basis function with the concepts of inner product and orthogonality

$$\begin{aligned} \left\langle U,R \right\rangle = \int _{a}^{b}U_{i}(x){D[U_{0}(X)+ \sum _{i=1}^{n}C_{i}U_{i}(x)]}\mathrm{{d}}x=0. \end{aligned}$$

These are sets of n-order linear equations which is solved to obtain all C i coefficients as follows:

$$\begin{aligned} \int _{0}^{1}(x-x^{4})(-24C_{1} -120C_{2}x +12C_{1}x^{2} + 20C_{2}x^{3} + 12x^{2})\mathrm{{d}}x=0 \end{aligned}$$

we obtain

$$\begin{aligned} -37/2 C_{2} - 207/35 C_{1} = -9/7. \end{aligned}$$
(29)

Also

$$\begin{aligned} \int _{0}^{1}(x-x^{5})(-24C_{1} -120C_{2}x +12C_{1}x^{2} + 20C_{2}x^{3} + 12x^{2})\mathrm{{d}}x=0 \end{aligned}$$

we get

$$\begin{aligned} -132/63 C_{2} - 13/2 C_{1} = -3/2 \end{aligned}$$
(30)

solving Eqs. (29) and (30) simultaneously to obtain \(C_{1}=-635/4331, C_{2}=504/4331\). Then we substitute these constants in (27) called the basis function and is the approximate solution we want

$$\begin{aligned} U(x)= 13x - 635/4331(x-x^{4}) + 504/4331(x-x^{5}) \end{aligned}$$

and

$$\begin{aligned} U(x)=56172/4331 x - 635/4331x^{4} - 504/4331x^{5}. \end{aligned}$$
(31)

Next we apply variational iteration method by constructing a correctional functional of (26)

$$\begin{aligned} t_{n+1}(x) = t_{n}(x) + \int _{0}^{x}\lambda (t^{(4)}_{n}(s) - t^{(2)}_{n}(s)-g(s)) \mathrm{{d}}s \end{aligned}$$

at \(n=0\)

$$\begin{aligned} t_{1}(x) = t_{0}(x) + \int _{0}^{x}\lambda (t^{(4)}_{0}(s) - t^{(2)}_{0}(s)-g(s)) \mathrm{{d}}s. \end{aligned}$$
(32)

We let

$$\begin{aligned} t_{0}(x)= U(x)= 13x - 635/4331(x-x^{4}) + 504/4331(x-x^{5} \end{aligned}$$
(33)

we differentiate (33), i.e \(t_{0}(x)\) successively to obtain it second and fourth derivative and substitute in the given Eq. (32) to have

$$\begin{aligned} t_{1}(x)&= 13x - 635/4331(x-x^{4}) + 504/4331(x-x^{5})\\&\quad + \int _{0}^{x}(s-x^{3})/25986 (56172x+5040x+3696x^{2}-840x^{3}+12x^{2}) \mathrm{{d}}s \end{aligned}$$
$$\begin{aligned} t_{1}(x)&= 1/4331(56172x + 635x^{4} - 504x^{5}) + 1/17324 (2540x^{4}-10080x^{5}\\ &\quad +7392x^{6}+1680x^{7})-1/51972(15240x^{2}-60480x^{3}+44352x^{4}+10080x^{5}) \end{aligned}$$

we simplify to get

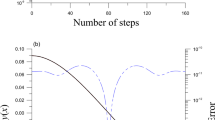
$$\begin{aligned} t_{1}(x)&= 12.96975294x -0.2932348187x^{2}+1.163703533x^{3}+0.7597475208x^{4}\nonumber \\&\quad -6.130182374x^{5}+4.267898383x^{6}+0.9699769053x^{7} . \end{aligned}$$
(34)

As the number of iterations increases, the function to be integrated is getting larger and cumbersome making the functions diverging from the analytical solutions at each iteration steps. Based on this fact, we apply the fixed point iterative technique where we use \(U_{1}(x)=y_{0}\) as a starting value after single iteration to avoid the use of arbitrary function (Fig. 1).

$$\begin{aligned} y_{n+1}^{(iv)}(x)=y_{n}^{\prime \prime }(x)-12x^{2} \end{aligned}$$

at \(n=0\)

$$\begin{aligned} y_{1}^{(iv)}(x)=y_{0}^{\prime \prime }(x)-12x^{2}. \end{aligned}$$
(35)

But

$$\begin{aligned} y_{0}(x)&=t_{1}(x) =12.96975294x -0.2932348187x^{2}+1.163703533x^{3}\nonumber \\&\quad +0.7597475208x^{4}-6.130182374x^{5}+4.267898383x^{6}+0.9699769053x^{7}. \end{aligned}$$
(36)

We differentiate (36) twice to get \(y_{0}^{\prime \prime }\) and then substituted it into the given Eq. (35) to obtain

$$\begin{aligned} y_{1}^{(iv)}=1/4331(-31492x^{2}-60480x^{3}-55440x^{4}-17640x^{5})-12x^{2}. \end{aligned}$$
(37)

To obtain \(y_{1}(x)\), we integrate (37) four times successively and imposing the boundary conditions to get

$$\begin{aligned} y_{1}(x)&=12.95702542x+0.07419139152x^{3}-x^{6}/30 +48/4331x^{7}-93/4331x^{8}\\&\quad -35/25986x^{9}. \end{aligned}$$

Repeat the process at \(n=2,3 \ldots\) until the iteration is terminated or convergence is achieved, after few iterations we get

$$\begin{aligned} y_{8}(x)&\,=\,12.95527250x+0.07483086130x^{3} +0.03742542966x^{5} -0.033333333x^{6}\\&\quad +\,0.00008908437939x^{7}-0.0005952380951x^{8}+0.000001237279890x^{9}\\&\quad -\,0.000006613756612x^{10}+1.124828201 \times 10^{-8}x^{11}-5.010421676 \times 10^{-8}x^{12}\\&\quad +\,7.208657571 \times 10^{-11}x^{13}-2752978943 \times 10^{-10}x^{14}+3.440595345 \times 10^{-13}x^{15}\\&\quad -\,1.147074559 \times 10^{-12}x^{16}+1.251515555 \times 10^{-15}x^{17}-3.748609670 \times 10^{-15}x^{18}\\&\quad -\,9.864762290 \times 10^{-18}x^{20}+1.093300832 \times 10^{-18}x^{21}-2.733252078 \times 10^{-19}x^{22}\\&\quad - \,1.890589383 \times 10^{-20}x^{23}. \end{aligned}$$

Thus we have Tables 1 and 2.

Table 1 For problem 1
Full size table
Table 2 For problem 2
Full size table
Fig. 1
figure 1

Example 1

Full size image
Fig. 2
figure 2

Example 2

Full size image

Discussion

The accuracy and convergence of the method are of great significance in a numerical experiment of such type. Accuracy measures the degree of closeness of the numerical solution to the theoretical solution while convergence measures even the closer approach of successive iteration to the exact solution as the number of iteration increases. To asses the success of our method, the scheme was tested with some numerical examples whose results presented as Tables 1 and 2. These tables show the comparison with exact method, Galerkin method, variational iteration method and the approximate solution obtained by variational-fixed point iteration method. It is observed that with few iterations, the order of the error is quite encouraging, which indicates fast rate of convergence. It is clearly seen that as the iterations proceeds, the error decreases and convergence is assured (Fig. 2).

Conclusion

In this paper we have shown the performance of the variational-fixed point iterative scheme for the solution three-point boundary value problems with help of some experiments which indicates to be very powerful and an efficient technique with good convergence property when compared with the existing method. We can conclude the method have an advantage over the existing methods.