Abstract
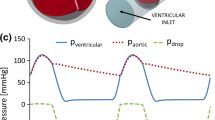
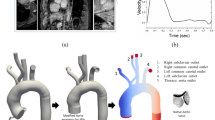
Mechanical heart valves (MHV) have been widely deployed as a routine surgical treatment option for patients with heart valve diseases due to its durability and performance. Understanding hemodynamics of MHV plays a key role in performance assessment as well as design. In this work, we propose a numerical method for simulations of full three dimensional MHV with moving valve leaflets in a typical human cardiac cycle. A cell-centered finite volume method is employed to model incompressible flows in MHV. As the flow experiences from laminar to turbulence over every cardiac cycle, the unsteady Reynolds average Navier–Stokes (URANS) equations is solved with \(k{-}\epsilon\) and Spalart–Allmaras turbulence models to resolve large scaled turbulent eddies in high Reynolds number flow regimes. URANS approach chosen for the balance of turbulence resolution and computational cost shows good agreement with more detailed turbulence models as well as experimental data. For capturing the large amplitude movement of the valves, we develop an optimization-based moving mesh technique with objective functions operating on different mesh quality metrics. The method is capable of extensively providing an effective way to maintain and improve the mesh quality due to large movement of domain boundaries. The numerical results for laminar and turbulent flows are validated against experimental data using Particle Image Velocimetry technique. The simulation is able to capture essential features of flows in MHV. The triple jet structure is observed in the simulations together with a switching of central orifice jet flow from horizontal axis to vertical axis downstream of the leaflets and the results are well compared with the experimental data. The moving mesh technique has enabled us to simulate a whole cardiac cycle with pulsatile physiological conditions and prescribed motions of the leaflets. The simulations can essentially reproduce the varying pressure profiles at the left ventricle and aorta. The wall shear stress and vorticity can then be deduced from the simulation results to further access the valve performance. This study also constitutes an important step towards understanding hemodynamics in MHV and contributing to the advancement in study of improved MHV.














Similar content being viewed by others
References
Aluri, S., and K. B. Chandran. Numerical simulation of mechanical mitral heart valve closure. Ann. Biomed. Eng. 29:665676, 2001.
Bluestein, D. W., S. Einav, and N. H. C. Hwang. A squeeze flow phenomenon at the closing of a bi-leaflet mechanical heart valve prosthesis. J. Biomech. 27:1369–1378, 1994.
Brewer, M., L. Diachin, P. Knupp, T. Leurent, and D. Melander. The mesquite mesh quality improvement toolkit. Proceedings of the 12th International Meshing Roundtable, Santa Fe NM, 2003, pp. 239–250.
Cheng, R., Y. G. Lai, and K. B. Chandran. Three-dimensional fluid-structure interaction simulation of bileaflet mechanical heart valve flow dynamics. Ann. Biomed. Eng. 32(11):1471–1483, 2004.
Dai, M., and D. P. Schmidt. Adaptive tetrahedral meshing in free-surface flow. J. Comput. Phys. 208(1):228252, 2005.
Dasi, L. P., L. Ge, H. A. Simon, F. Sotiropoulos, and A. P. Yoganathan, Vorticity dynamics of a bileaflet mechanical heart valve in an axisymmetric aorta. Phys. Fluids 19(6), 2007.
Dumont, K. Comparison of the hemodynamic and thrombogenic performance of two bileaflet mechanical heart valves using a CFD/FSI model. ASME J. Biomech. Eng. 129:0148–0731, 2007.
Ferziger, J. H., and M. Peric. Computational Methods for Fluid Dynamics. Berlin: Springer, 1995.
Friedewald, V. E., R. O. Bonow, J. S. Borer, B. A. Carabello, P. P. Kleine, C. W. Akins, W. C. Roberts. The editor’s roundtable: cardiac valve surgery. Am. J. Cardiol. 99:1269–1278, 2007.
Fukuta H., and W. C. Little: The cardiac cycle and the physiological basis of left ventricular contraction, ejection, relaxation, and filling. Heart Failure Clin. 4(1):111, 2008.
Ge, L., H. L. Leo, F. Sotiropoulos, and A. P. Yoganathan. Flow in a mechanical bileaflet heart valve at laminar and near-peak systole flow rates: CFD simulations and experiments. J. Biomech. Eng. 127(5):782–797, 2005.
Jamieson, W. R. Current and advanced prostheses for cardiac valvular replacement and reconstruction surgery. Surg. Technol. Int. 10:121–149, 2002.
King, M. J., J. Gorden, T. David, and J. Fisher. A three-dimensional, time-dependent analysis of flow through a bileaflet mechanical heart valve: comparison of experimental and numerical results. J. Biomech. 29(5):609–618, 1996.
King, M. J., T. David, and J. Fisher. Three-dimensional study of the effect of two leaflet opening angles on the time-dependent flow through a bileaflet mechanical heart valve. Med. Eng. Phys. 19(3):235–241, 1997.
Lai, Y. G., K. B. Chandran, and J. Lemmon. A numerical simulation of mechanical heart valve closure fluid dynamics. J. Biomech. 35:881–892, 2002.
Lee, C. S., and K. B. Chandran. Numerical simulation of instantaneous back flow through central clearance of bi-leaflet mechanical heart valve at closure: shear stresses and pressure fields. Med. Biol. Eng. Comput. 33(3):257–263, 1995.
Lohner, R., and C. Yang. Improved ALE mesh velocities for moving bodies. Commun. Numer. Methods Eng. 12:599–608, 1996.
Lomtev, I., R. M. Kirby, and G. E. Karniadakis. A discontinuous Galerkin ALE method for compressible viscous flows in moving domains. J. Comput. Phys. 155:128–159, 1999.
Nkomo, V. T., J. M. Gardin, T. N. Skelton, J. S. Gottdiener, C. G. Scott, and M. Enriquez-Sarano. Burden of valvular heart diseases: a population-based study. Lancet 368:1005–1011, 2006.
Peskin, C. S. Flow patterns around heart valves: a numerical method. J. Comput. Phys. 10(2):252–271, 1972.
Peskin, C.S. The fluid-dynamics of heart-valves- experimental, theoretical, and computational methods. Annu. Rev. Fluid Mech. 14:235, 1982.
Reif, T. H. A numerical analysis of back flow between the leaflets of St Jude medical cardiac valve prostheses. J. Biomech. 24(8):733–741, 1991.
Spalart, P. R. Trends in Turbulence Treatments, AIAA 2000-2306, 2000.
Shih, T.-H., W. W. Liou, A. Shabbir, Z. Yang, and J. Zhu. A New Eddy-Viscosity model for high Reynolds number turbulent flows—model development and validation. Comput. Fluids 24(3):227–238, 1995.
Simon, H. A., L. Ge, F. Sotiropoulos, and A. P. Yoganathan. Simulation of the three-dimensional hinge flow fields of a bileaflet mechanical heart valve under aortic conditions. Ann. Biomed. Eng. 38(3):841–853, 2010.
Turitto, V. T., and C. L. Hall. Mechanical factors influencing hemostasis and thrombosis. Thromb. Res. 92:25–31, 1998 .
Vongpatanasin, W., D. L. Hillis, and R. A. Lange. Prosthetic heart valves. New Engl. J. Med. 335:407–416, 1996.
Weller, H. G., G. Tabor, H. Jasak, and C. Fureby. A tensorial approach to computational continuum mechanics using object orientated techniques. Comput. Phys. 12(6):620631, 1998.
Yakhot, V., and S. A. Orszag. Renormalization group analysis of turbulence: I. Basic theory. J. Sci. Comput. 1(1):1–51, 1986.
Acknowledgments
The authors are grateful to Professor Yeo Joon Hock of the School of Mechanical & Aerospace Engineering at Nanyang Technology University, Singapore, for arranging access to his Particle Imaging Velocimetry equipment. This work was supported primarily by a research grant from the Ministry of Education, Singapore (MOE) AcRF Tier 1 (R-397-000-085-133).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Yi-Ren Woo.
Rights and permissions
About this article
Cite this article
Nguyen, VT., Kuan, Y.H., Chen, PY. et al. Experimentally Validated Hemodynamics Simulations of Mechanical Heart Valves in Three Dimensions. Cardiovasc Eng Tech 3, 88–100 (2012). https://doi.org/10.1007/s13239-011-0077-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13239-011-0077-z