A photogrammetry-based method to measure total and local volume changes of unsaturated soils during triaxial testing

Abstract

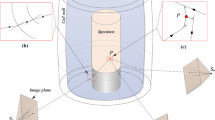
Triaxial tests have been widely used to evaluate soil behaviors. In the past few decades, several methods have been developed to measure the volume changes of unsaturated soil specimens during triaxial tests. Literature review indicates that until now it remains a major challenge for researchers to measure the volume changes of unsaturated soil specimens during triaxial testing. This paper presents a non-contact method to measure the total and local volume changes of unsaturated soil specimens using a conventional triaxial test apparatus for saturated soils. The method is simple and cost-effective, requiring only a commercially available digital camera to take images of an unsaturated soil specimen during triaxial testing from which accurate 3D model of the soil specimen is reconstructed. In this proposed method, the photogrammetric technique is utilized to determine the orientations of the camera where the images are taken and the shape and location of the acrylic cell, multiple optical ray tracings are employed to correct the refraction at the air-acrylic cell and acrylic cell–water interfaces, and a least-square optimization technique is applied to estimate the coordinates of any point on the specimen surface. The paper first discusses the theoretical aspects of the proposed method. An image analysis on a caliper was then used to evaluate the accuracy of photogrammetric analysis in the air. A series of isotropic compression tests on a stainless steel cylinder were used to demonstrate the procedure and evaluate the accuracy of the proposed method, while triaxial shearing tests on a saturated sand specimen were used to exam the capacity of the proposed method for measuring the total and localized volume changes during triaxial testing. Results obtained from the validation tests indicate that the accuracy for the photogrammetry in the air is about 10 µm. The average accuracy for single point measurements in the triaxial tests ranges from 0.056 to 0.076 mm with standard deviations varying from 0.033 to 0.061 mm. The accuracy for total volume measurements is better than 0.25 %.

Appendix

1.1 Derivation of the Snell’s law in the 3D space

The scalar form of the Snell’s law is normally expressed as follows [41]:

$$ \frac{{n_{1} }}{{n_{2} }} = \frac{{\sin \theta_{2} }}{{\sin \theta_{1} }} $$

(31)

where $n_{1} \,{\text{and}}\,n_{2}$ = refraction indices for two media, and $\theta_{1} \,{\text{and}}\,\theta_{2}$ = incident and refraction angles with respect to the normal at the refractive boundary.

In the proposed method, incident and refractive rays are often expressed as vectors in 3D space. As a result, it is more convenient to use the vector form of Snell’s law. Its derivations are as follows:$\overrightarrow {i}$ and $\overrightarrow {r}$ are unit directional vectors in space for the incident and refractive rays as shown in the Fig. 20, respectively. $\overrightarrow {n}$ is the surface normal to the refractive boundary at the intersection point and also a unit directional vector pointing to the side of the incident ray. To facilitate the discussion, both $\overrightarrow {i}$ and $\overrightarrow {r}$ are first resolved into two components: one is parallel to n and the other is perpendicular to n.

$$ \overrightarrow {i} = \overrightarrow {{i_{ \bot } }} + \overrightarrow {{i_{\parallel } }} $$

(32)

$$ \overrightarrow {r} = \overrightarrow {{r_{ \bot } }} + \overrightarrow {{r_{\parallel } }} $$

(33)

where subscripts “$\bot$” and “$\parallel$” represents direction parallel to and perpendicular to $\overrightarrow {n}$, respectively.

Fig. 20

Snell’s law

It is worth noting that $\theta_{1} \,{\text{and}}\,\theta_{2}$ are scalars and have ranges from 0 to 90°. Consequently, the following relationships exist:

$$ \overrightarrow {i} \cdot \overrightarrow {n} = - \cos \theta_{1} $$

(34)

$$ \left| {\overrightarrow {{i_{\parallel } }} } \right| = \sin \theta_{1} $$

(35)

$$ \left| {\overrightarrow {{r_{\parallel } }} } \right| = \sin \theta_{2} $$

(36)

Both $\overrightarrow {{i_{ \bot } }} {\text{ and }}\overrightarrow {{r_{ \bot } }}$ are parallel to $\overrightarrow {n}$ but with opposite direction; therefore, they can be expressed as follows:

$$ \overrightarrow {{i_{ \bot } }} = - \cos \theta_{1} \overrightarrow {n} $$

(37)

$$ \overrightarrow {{r_{ \bot } }} = - \cos \theta_{2} \overrightarrow {n} $$

(38)

Combining Eqs. 32 and 36, one has

$$ \overrightarrow {{i_{\parallel } }} = \overrightarrow {i} - \overrightarrow {{i_{ \bot } }} = \overrightarrow {i} + \cos \theta_{1} \overrightarrow {n} $$

(39)

$\overrightarrow {{i_{\parallel } }} {\text{ and }}\overrightarrow {{r_{\parallel } }}$ are also parallel to each other. Therefore,

$$ \overrightarrow {{r_{\parallel } }} = \left| {\overrightarrow {{r_{\parallel } }} } \right|\frac{{\overrightarrow {{i_{\parallel } }} }}{{\left| {\overrightarrow {{i_{\parallel } }} } \right|}} = \sin \theta_{2} \frac{{\overrightarrow {{i_{\parallel } }} }}{{\sin \theta_{1} }} = \frac{{\sin \theta_{2} }}{{\sin \theta_{1} }}\left( {\overrightarrow {i} + \cos \theta_{1} \overrightarrow {n} } \right) $$

(40)

Plugging Eqs. 31 and 34 into Eq. 40, one has

$$ \overrightarrow {{r_{\parallel } }} = \frac{{n_{1} }}{{n_{2} }}\left[ {\overrightarrow {i} - \left( {\overrightarrow {i} \cdot \overrightarrow {n} } \right)\overrightarrow {n} } \right] $$

(41)

Combining Eqs. 31, 34, and 38, one has

$$ \begin{aligned} \overrightarrow {{r_{ \bot } }} & = - \cos \theta_{2} \overrightarrow {n} = - \sqrt {1 - \sin^{2} \theta_{2} } \overrightarrow {n} = - \sqrt {1 - \left( {\frac{{n_{1} }}{{n_{2} }}\sin \theta_{1} } \right)^{2} } \overrightarrow {n} = - \sqrt {1 - \left( {\frac{{n_{1} }}{{n_{2} }}} \right)^{2} \left( {1 - \cos^{2} \theta_{1} } \right)} \overrightarrow {n} \\ & \quad = - \sqrt {1 - \left( {\frac{{n_{1} }}{{n_{2} }}} \right)^{2} \left[ {1 - \left( {\overrightarrow {i} \cdot \overrightarrow {n} } \right)^{2} } \right]} \overrightarrow {n} \\ \end{aligned} $$

(42)

Substituting Eqs. 40 and 41 into Eq. 33 yields:

$$ \overrightarrow {r} = \frac{{n_{1} }}{{n_{2} }}\overrightarrow {i} - \left( {\frac{{n_{1} }}{{n_{2} }}\left( {\overrightarrow {i} \cdot \overrightarrow {n} } \right) + \sqrt {1 - \left( {\frac{{n_{1} }}{{n_{2} }}} \right)^{2} \left[ {1 - \left( {\overrightarrow {i} \cdot \overrightarrow {n} } \right)^{2} } \right]} } \right)\overrightarrow {n} $$

(43)

Equation 43 requires four inputs to calculate the unit vector for the refractive ray $\overrightarrow {r}$: $\overrightarrow {i}$, $\overrightarrow {n}$, $n_{1} \,{\text{and}}\,n_{2}$.