Numerical simulation of interaction between hydraulic and natural fractures in discontinuous media

Abstract

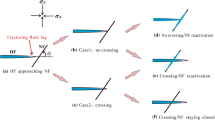
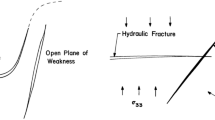
In this study, the displacement discontinuity formulation is used to solve the problem of interaction between hydraulic fractures (HF) and natural fractures (NF). Furthermore, a numerical program (2DFPM) is developed to study the mechanical activation of a NF because of the propagation of the HF. The accuracy of the numerical method is enhanced using the higher-order displacement variation along the HF and the special crack tip element near its ends. The maximum tangential stress criterion is implemented to predict the HF propagation path, and the stages of hydraulic fracturing tip approaching, coalescence and fluid penetration along the NF are modeled. The tangential stress around the NF with different contact modes (bonded, sliding and opening) is calculated by coupling the finite difference and boundary element methods. The location of secondary tensile fracture that re-initiates along the opposite side of NF is determined, and the key parameters that have great influence on interaction process are discussed. The results show that position, distance and inclination of the HF relative to the pre-existing discontinuity have a strong influence on the HF propagation path.

Appendix

The tangential stresses σ ⁱ⁺ _t and σ ⁱ⁻ _t on the both side of the ith element of the crack can be written in the following form:

$$ {\mathop \sigma \limits^{i}}_{t}^{ + } = \frac{1}{2}({\mathop \sigma \limits^{i}}_{t}^{ - } + {\mathop \sigma \limits^{i}}_{t}^{ + } ) - \frac{1}{2}({\mathop \sigma \limits^{i}}_{t}^{ - } - {\mathop \sigma \limits^{i}}_{t}^{ + } ),\quad {\mathop \sigma \limits^{i}}_{t}^{ - } = \frac{1}{2}({\mathop \sigma \limits^{i}}_{t}^{ - } + {\mathop \sigma \limits^{i}}_{t}^{ + } ) + \frac{1}{2}({\mathop \sigma \limits^{i}}_{t}^{ - } - {\mathop \sigma \limits^{i}}_{t}^{ + } ) $$

where

$$ \begin{aligned} {\mathop \sigma \limits^{i}}_{t}^{ - } - {\mathop \sigma \limits^{i}}_{t}^{ + } = &\frac{2G}{1 - \nu }\left[ {\left\{ {{\mathop D\limits^{i + 1}}_{s} \cos ({\mathop \beta \limits^{i + 1}} - {\mathop \beta \limits^{i} }) - {\mathop D\limits^{i - 1}}_{s} \cos ({\mathop \beta \limits^{i}} - {\mathop \beta \limits^{i - 1}} )} \right\}/{\mathop {\varDelta s}\limits^{i} }} \right] \hfill \\& - \frac{2G}{1 - \nu }\left[ {\left\{ {{\mathop D\limits^{i + 1}}_{n} \sin ({\mathop \beta \limits^{i + 1}} - {\mathop \beta \limits^{i}} ) + {\mathop D\limits^{i - 1}}_{n} \sin ({\mathop \beta \limits^{i}} - {\mathop \beta \limits^{i - 1}} )} \right\}/{\mathop {\varDelta s}\limits^{i} }} \right] \hfill \\ \end{aligned} $$

where β is the inclination angle of the elements and

$$ {\mathop {\varDelta s}\limits^{i}} = {\mathop a\limits^{i - 1}} \cos ({\mathop \beta \limits^{i}} -{ \mathop \beta \limits^{i - 1}} ) + {\mathop {2a}\limits^{i}} + {\mathop a\limits^{i + 1} }\cos ({\mathop \beta \limits^{i + 1}} - {\mathop \beta \limits^{i}} ) $$

In which, the term $\frac{1}{2}({\mathop {\sigma_{t} }\limits^{i}}^{ - } + {\mathop {\sigma_{t} }\limits^{i}}^{ + } )$ is continues. This term represents the combined effects of the N elemental displacement discontinuities along the boundary and is written [8]:

$$ \begin{aligned} \frac{1}{2}({\mathop \sigma \limits^{i}}_{t}^{ - } + {\mathop \sigma \limits^{i}}_{t}^{ + }) & = 2G\sum\limits_{j = 1}^{N} {\left[ {2\cos^{2} \gamma \bar{F}_{4} - \sin 2\gamma \bar{F}_{5} + \bar{y}(\cos 2\gamma \bar{F}_{6} + \sin 2\gamma \bar{F}_{7} )} \right]} {\mathop D\limits^{i}}_{s} \hfill \\ & quad+ 2G\sum\limits_{j = 1}^{N} {\left[ { - \bar{F}_{5} - \bar{y}(\sin 2\gamma \bar{F}_{6} - \cos 2\gamma \bar{F}_{7} )} \right]} {\mathop D\limits^{i}}_{n} \hfill \\ \end{aligned} $$

then

$$ \begin{aligned} &{\mathop {\sigma_{t} }\limits^{i}}^{ + } = \sum\limits_{j = 1}^{N} {A_{{_{ts} }}^{ij} D_{s}^{j} + \sum\limits_{j = 1}^{N} {A_{{_{tn} }}^{ij} \,D_{n}^{j} } } - \frac{1}{2}({\mathop \sigma \limits^{i}}_{t}^{ - } - {\mathop \sigma \limits^{i}}_{t}^{ + } ) \hfill \\ &{\mathop {\sigma_{t} }\limits^{i}}^{ - } = \sum\limits_{j = 1}^{N} {A_{{_{ts} }}^{ij} D_{s}^{j} + \sum\limits_{j = 1}^{N} {A_{{_{tn} }}^{ij} \,D_{n}^{j} } } + \frac{1}{2}({\mathop \sigma \limits^{i}}_{t}^{ - } - {\mathop \sigma \limits^{i}}_{t}^{ + } ) \hfill \\ \end{aligned} $$

The maximum principal stress is calculated along the frictional interface at points between successive elements from the normal, shear and tangential stresses. The maximum principal stress is determined above and below the interfaces from the respective normal and shear stresses.

$$ \sigma_{1}^{ \pm } = \frac{{\sigma_{xx}^{ \pm } + \sigma_{yy} }}{2} + \sqrt {\left( {\frac{{\sigma_{xx}^{ \pm } - \sigma_{yy} }}{2}} \right)^{2} + \sigma_{yx} } $$

When the maximum tensile stress (σ ₁) exceeds the tensile strength of the rock, a new fracture will grow perpendicular to the direction of maximum tension. The new splay crack is oriented at an angle α from the frictional interface that is π/2 from the orientation of the maximum tensile stress.

$$ \alpha_{1}^{ \pm } = \frac{\pi }{2} + \frac{1}{2}\tan^{ - 1} \left[ {\frac{{2\sigma_{yx} }}{{\sigma_{xx}^{ \pm } - \sigma_{yy} }}} \right] $$