A North-South Trade Model of Offshoring and Unemployment

Abstract

This paper analyzes a North-South trade model with offshoring and unemployment due to union wage setting. A reduction in the cost of offshoring decreases employment in the North except possibly if there is little offshoring initially. If the scale of Northern firms also falls, then each Northern agent’s welfare declines. Unions have an incentive to reduce their own bargaining power by strategically delegating wage negotiation so as to cushion the negative employment effects.

Appendices

Appendix A: Proofs

Maximization of the Nash Product Maximizing the Nash product is equivalent to solving

$$\max\limits_{\frac{w^{N}}{P} > b^{\frac{1}{\beta}}} : (- \varepsilon + \gamma) \ln \left(\frac{w^{N}}{P} \right) + (1 - \gamma) \ln \left[ \left(\frac{w^{N}}{P} \right)^{\beta} - b \right] . $$

Setting the derivative of the objective function equal to zero gives

$$\left(\frac{w^{N}}{P} \right)^{-1} \left[ - (\varepsilon - \gamma) + \beta (1 - \gamma) \frac{\left(\frac{w^{N}}{P} \right)^{\beta}}{\left(\frac{w^{N}}{P} \right)^{\beta} - b} \right] = 0 . $$

Equation 7 is the solution to this first-order condition. The term in brackets and, therefore, the derivative of the objective function are monotonically decreasing functions. So the first-order condition yields the global maximum of the Nash product.

Proof of Proposition 1

The function f defined in Eq. 9 maps (0, n−n ^S] or [0, n−n ^S] to $\mathbb {R}_{+}$, depending on whether n ^S = 0 or n ^S>0. f is continuous and monotonically decreasing. It satisfies f(0)>1 for n ^S>0 (from Eq. 10) and goes to infinity as n ^M→0 for n ^S = 0.

The function g defined in Eq. 11 maps the set of (n ^M, f ^M)-values for which the term in square brackets in Eq. 11 is positive, i.e.,

$$ \left\{ (n^{M} , \, f^{M}) \in \mathbb{R}^{2}_{+} \left| \, \, n^{M} < \frac{1}{\varepsilon} \left[ \frac{\bar L^{S}}{f^{M}} - (\varepsilon - 1) \alpha^{- \varepsilon} n^{S} \right] \right. \right \} , $$

(24)

on $\mathbb {R}_{+}$. This set is non-empty if either n ^S = 0 or n ^S>0 and

$$ f^{M} < \frac{\alpha^{\varepsilon} \bar L^{S}}{(\varepsilon - 1) n^{S}} . $$

(25)

Since $\bar L^{S} / f^{M} > n^{M}$ for all (n ^M, f ^M) in Eq. 24, g(n ^M, f ^M) is monotonically increasing in n ^M and decreasing in f ^M. It diverges to infinity, as n ^M approaches the upper bound in Eq. 24. If n ^S>0 and f ^M is so large that Eq. 25 is violated, then offshoring generally does not pay. This follows from the fact that, from Eq. 8,

$$\left(\frac{w^{N} a^{N}}{w^{S} a^{S}} \right)^{\varepsilon} a^{S} x^{N} \leq (\varepsilon - 1) f^{M} , $$

so that Eq. 6 holds with strict inequality for all n ^M≥0.

We proceed to check under which conditions a solution to Eq. 9 and Eq. 11 exists. As argued in the main text, to establish existence of equilibrium, it then merely remains to show that there is positive unemployment. We start with the case n ^S>0.

Suppose first f ^M is large, in that it violates (25). Then there is an equilibrium with n ^M = 0 and (w ^N a ^N)/(w ^S a ^S)=f(0) (>1). This follows immediately from the fact that offshoring is not profitable in this case.

Next, let f ^M satisfy (25), so that the domain of g(n ^M, f ^M) is non-empty. Suppose further that

$$ f^{M} \geq \frac{\alpha^{\varepsilon} \bar L^{S}}{(\varepsilon - 1) n^{S}} \left[ 1 - \frac{n^{S}}{(\omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S})} \right] = \bar{f}^{M} $$

(26)

(>0 due to Eq. 10). From Eq. 9 and 11, this implies f(0)≤g(0, f ^M). Graphically, the abscissa intercept of f(n ^M) is closer to the origin than the abscissa intercept of g(n ^M, f ^M). Again there is an equilibrium with n ^M = 0 and (w ^N a ^N)/(w ^S a ^S)=f(0) (>1). The fact that (w ^N a ^N)/(w ^S a ^S)≤g(0, f ^M) implies that offshoring is not profitable (cf. (11)).

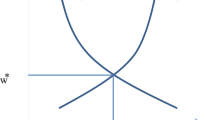
For $f^{M} < \bar {f}^{M}$, we have f(0)>g(0, f ^M). Since g(n ^M, f ^M) diverges to infinity, continuity implies that f(n ^M) and g(n ^M, f ^M) intersect at some n ^M>0. As f(n ^M) is decreasing and g(n ^M, f ^M) is increasing in n ^M, the intersection is unique (see Fig. 1). The condition n ^M<n−n ^S is satisfied if f(n−n ^S)<g(n−n ^S, f ^M). From Eq. 9 and 10, f(n−n ^S)>1. g(n−n ^S, f ^M) is monotonically decreasing in f ^M and converges to unity for f ^M→0. So there is $\underline {f}^{M}$ ($0 < \underline {f}^{M} < \bar {f}^{M}$) such that $f (n - n^{S}) = g (n - n^{S} , \underline {f}^{M})$ and n ^M<n−n ^S exactly if $f^{M} > \underline {f}^{M}$.

The case n ^S = 0 is analogous to the case with n ^S>0 and $f^{M} < \bar {f}^{M}$. Since f(n ^M) goes to infinity as n ^M goes to zero, there is an intersection with g(n ^M, f ^M). By the same argument as in the preceding paragraph, there is $\underline {f}^{M}$ ($0 < \underline {f}^{M} < \bar {f}^{M}$) such that n ^M<n−n ^S exactly if $f^{M} > \underline {f}^{M}$.

The denominators of the fractions on the right-hand side of Eq. 12 are non-zero, due to Eq. 10 and the fact that n ^M>0 if n ^S = 0. Let $\underline {\bar L}^{N}$ denote the right-hand side of Eq. 12 evaluated at f ^M and the ensuing amount of offshoring n ^M. Then $\bar L^{N} > \underline {\bar L}^{N}$ implies the presence of unemployment. □

Comparative Statics Effects of f ^M on n ^M Whenever n ^M>0, n ^M satisfies f(n ^M)=g(n ^M, f ^M), i.e.,

$$ \frac{f^{M}}{\bar L^{S} - n^{M} f^{M}} = \frac{1}{\varepsilon - 1} \frac{1}{\alpha^{- \varepsilon} n^{S} + n^{M}} \frac{(\omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S}) - n^{S}}{(\omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S} - n^{M})} . $$

(27)

Differentiating (27) totally proves

$$\begin{array}{@{}rcl@{}} \frac{dn^{M}}{df^{M}} & = & - \frac{\bar L^{S}}{f^{M} \left(\bar L^{S} - n^{M} f^{M} \right)} \bigg[ \frac{f^{M}}{\bar L^{S} - n^{M} f^{M}} \\ & & + \frac{1}{\alpha^{- \varepsilon} n^{S} + n^{M}} + \frac{\alpha^{\varepsilon - 1}}{(\omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S} - n^{M})} \bigg]^{-1} < 0 . \end{array} $$

(28)

For future reference, define ${\Phi } : (\underline {f}^{M} , \infty ) \rightarrow \mathbb {R}_{+}$ as the function that assigns equilibrium values of n ^M to f ^M. As shown above ${\Phi }^{\prime } (f^{M}) < 0$ whenever Φ(f ^M)>0.

Since, by definition, ${\Phi } (\underline {f}^{M}) = n - n^{S}$, we have Φ(f ^M)<n−n ^S for $f^{M} > \underline {f}^{M}$. The fact that (n ^M, f ^M) is in Eq. 24 implies $n^{M} < \bar L^{S} / f^{M}$ and, hence, Φ(f ^M)→0 for $f^{M} \to \infty$ if n ^S = 0.

Proof of Proposition 2

Define the right-hand side of Eq. 12 as ψ(n ^M, f ^M). ψ maps $\{ (n^{M} , f^{M}) \in \mathbb {R}^{2}_{+} | \, \, n_{M} \leq \min \{ n - n^{S} , \, \bar L^{S} / f^{M} \} \}$ on $\mathbb {R}_{+}$. As just seen, Φ(f ^M)<n−n ^S and ${\Phi } (f^{M}) < \bar L^{S} / f^{M}$. So the composite function ${\Gamma } (f^{M}) = \psi ({\Phi } (f^{M}) , \, f^{M}) : (\underline {f}^{M} , \infty ) \rightarrow \mathbb {R}_{+}$ gives the reduced-form relationship between the cost of offshoring and aggregate employment.

Log-differentiating Γ, using Eq. 12, evaluating the derivative at $\bar {f}^{M}$ (interpreting ${\Phi }^{\prime } (\bar {f}^{M})$ as the left-hand derivative), and using Eq. 26, we obtain

$$\begin{array}{@{}rcl@{}} \frac{d \ln {\Gamma} (\bar{f}^{M})}{df^{M}} & = & {\Phi}^{\prime} (\bar{f}^{M}) \bigg\{ - \frac{1}{n - n^{S}} - \frac{\alpha^{\varepsilon}}{(\varepsilon - 1) n^{S}} + \frac{\alpha^{\varepsilon}}{(\varepsilon - 1) \left[ (\omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S}) \right]} \\ & & \qquad \qquad - \frac{\alpha^{\varepsilon} }{n^{S}} + \frac{\alpha^{\varepsilon - 2}}{n^{S}} - \frac{\alpha^{\varepsilon - 2}}{(\omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S})} \bigg\} . \end{array} $$

(29)

The term in braces is positive if, and only if, the conditions of the proposition are satisfied. Given ${\Phi }^{\prime } (\bar {f}^{M}) < 0$, this proves the proposition. □

For n ^S small enough, the sign of the term in braces in Eq. 29 is determined by the three 1/n ^S-terms. The fact that it is positive for n ^S small enough is due to the fact that the final, positive, term dominates. This is because α ^ε−2>α ^ε/(ε−1)+α ^ε (=α ^ε−1). Tracing it back through the steps leading to Eq. 29, we find that this final term stems from log-differentiating the term (n ^S+α ^ε−1 n ^M)^1/α in Eq. 12 with respect to n ^M. This term, in turn, results from substituting for (w ^N a ^N)/(w ^S a ^S) from Eq. 9 into Eq. 8 to obtain x ^N. Thus, ${\Gamma }^{\prime } (f^{M}) < 0$ for f ^M sufficiently close to $\bar {f}^{M}$ and n ^S small enough is ultimately due to the strong negative impact of an increase in n ^M on relative production cost.

The Model with Full Employment For the sake of brevity, we confine attention to the case n ^S = 0. The condition that the wage rate and employment maximize the Nash product is replaced with the labor market clearing condition $\bar L^{N} = (n - n^{M}) a^{N} x^{N}$ in the definition of equilibrium. Full employment in both countries and (4) yield

$$\frac{w^{N} a^{N}}{w^{S} a^{S}} = \left(\frac{a^{N}}{a^{S}} \frac{\bar L^{S} - n^{M} f^{M}}{\bar L^{N}} \frac{n - n^{M}}{n^{M}} \right)^{\frac{1}{\varepsilon}} . $$

This equation and Eq. 11 with n ^S = 0 jointly determine the equilibrium values of (w ^N a ^N)/(w ^S a ^S) and n ^M. The equilibrium mass of MNEs n ^M satisfies

$$ \frac{n^{M} f^{M}}{\frac{\bar L^{S}}{n^{M}} - \varepsilon f^{M}} = \left(\frac{a^{N}}{a^{S}} \frac{n - n^{M}}{\bar L^{N}} \right)^{\alpha} \left(\frac{n^{M}}{\bar L^{S} - n^{M} f^{M}} \right)^{1 - \alpha} n^{M} f^{M} . $$

(30)

From Eq. 11, $n^{M} < \bar L^{S} / (\varepsilon f^{M})$. From Eqs. 5 and 11, the equilibrium real wage rate w ^N/P is determined by

$$ \left(\frac{w^{N} a^{N}}{\alpha P} \right)^{\varepsilon - 1} = n + (\varepsilon - 1) \frac{n^{M} f^{M}}{\frac{\bar L^{S}}{n^{M}} - \varepsilon f^{M}} . $$

(31)

The right-hand side of Eq. 30 is zero for f ^M = 0. It also converges to zero for $f^{M} \to \infty$. This follows from the fact that n ^M ($< \bar L^{S} / (\varepsilon f^{M})$) goes to zero and n ^M f ^M ($< \bar L^{S} / \varepsilon$) is bounded. So from Eq. 31, the real wage in the North satisfies w ^N/P = α n ^1/(ε−1)/a ^N for f ^M = 0, w ^N/P>α n ^1/(ε−1)/a ^N for f ^M>0, and w ^N/P→α n ^1/(ε−1)/a ^N for $f^{M} \to \infty$.

Proof of Proposition 3

Let ${\Lambda } (f^{M}) = {\Gamma } (f^{M}) / [n - n^{S} - {\Phi } (f^{M})] : (\underline {f}^{M} , \infty ) \rightarrow \mathbb {R}_{+}$. Λ gives the equilibrium value of L ^N/(n−n ^S−n ^M), so the derivative of equilibrium real profit with respect to f ^M has the same sign as

$$ \frac{d \ln {\Lambda} (f^{M})}{df^{M}} = \frac{d \ln {\Gamma} (f^{M})}{df^{M}} + \frac{{\Phi}^{\prime} (f^{M})}{n - n^{S} - {\Phi} (f^{M})} . $$

(32)

${\Phi }^{\prime } (f^{M}) < 0$, ${\Gamma }^{\prime } (f^{M}) < 0$, and d f ^M<0 jointly imply $d\ln {\Lambda } (f^{M}) > 0$. □

Proof of Proposition 4

From Eqs. 29, 32, and ${\Phi } (\bar {f}^{M}) = 0$,

$$\begin{array}{@{}rcl@{}} \frac{d \ln {\Lambda} (\bar{f}^{M})}{df^{M}} & = & {\Phi}^{\prime} (\bar{f}^{M}) \bigg\{ - \frac{\alpha^{\varepsilon}}{(\varepsilon - 1) n^{S}} + \frac{\alpha^{\varepsilon}}{(\varepsilon - 1) \left[ (\omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S}) \right]} \\ & & \qquad \qquad - \frac{\alpha^{\varepsilon} }{n^{S}} + \frac{\alpha^{\varepsilon - 2}}{n^{S}} - \frac{\alpha^{\varepsilon - 2}}{(\omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S})} \bigg\} . \end{array} $$

Condition (15) implies that the term in braces is negative. Jointly with ${\Phi }^{\prime } (\bar {f}^{M}) < 0$, it follows that $d \ln {\Lambda } (\bar {f}^{M}) / df^{M} > 0$. □

Proof of Proposition 5

Using Eq. 3, markup pricing, (7), and L ^N = (n−n ^S−n ^M)a ^N x ^N, real world income can be written as

$$\frac{I}{P} = \left(\frac{\omega^{N}}{\alpha} \right)^{\varepsilon} \frac{L^{N}}{a^{N} (n - n^{S} - n^{M})} . $$

So the derivative of social welfare with respect to f ^M at $\bar {f}^{M}$ has the same sign as $d \ln {\Lambda } (\bar {f}^{M}) / df^{M}$, which is positive under the conditions of Proposition 4. □

Impact of Imitation on Utilitarian Social Welfare World income I/P is given by the expression above with n ^M = 0. An increase in n ^S raises Utilitarian social welfare if, and only if, it raises L ^N/(n−n ^S). From Eq. 12 with n ^M = f ^M = 0, this is the case exactly if

$$\alpha^{\varepsilon} \varepsilon n^{S} > (\omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S}) - n^{S} . $$

Reasons for δ < 1 One interpretation for why the PUL sets a real wage below the RTM level is that the union appoints a weak union leader, with bargaining power $1 - \tilde \gamma \in [0 , \, 1 - \gamma )$. The wage rate the weak union leader agrees to in the wage bargain is given by Eq. 7 with γ replaced by $\tilde \gamma$. Setting

$$\delta = \left[ 1 - \frac{\beta (1 - \gamma)}{\varepsilon - \gamma} \right]^{\frac{1}{\beta}} \left[1 - \frac{\beta (1 - \tilde \gamma)}{\varepsilon - \tilde \gamma} \right]^{- \frac{1}{\beta}} $$

(<1) yields (16). The first term in the product on the right-hand side is $\underline \delta$, so $\delta > \underline \delta$.

A second possible interpretation is that the PUL maximizes union members’ expected utility, but uses a lower reservation utility for the unemployed $\tilde b$ in doing so. Replacing b with $\tilde b$ in Eq. 7 and setting

$$\delta = \left(\frac{\tilde b}{b} \right)^{\frac{1}{\beta}} $$

(<1) again yields (16). To make sure that $\delta \geq \underline \delta$, we have to assume $\tilde b \geq \underline \delta ^{\beta } b$.

Third, suppose the union delegates wage bargaining to a PUL with $1 - \tilde \beta \not = 1 - \beta$. The wage he negotiates is given by Eq. 7 with β replaced with $\tilde \beta$. Equation 16 is obtained by setting

$$\delta = \left\{ \left[ 1 - \frac{\beta (1 - \gamma)}{\varepsilon - \gamma} \right] b^{- 1} \right\}^{\frac{1}{\beta}} \left\{ \left[1 - \frac{\tilde \beta (1 - \gamma)}{\varepsilon - \tilde \gamma} \right]^{-1} \tilde b \right\}^{\frac{1}{\tilde \beta}} . $$

The second factor on the right-hand side is the wage negotiated by the PUL. It is not generally a monotonic function of $\tilde \beta$. Its derivative with respect to $\tilde \beta$ has the same sign as $z - 1 - \ln z - \ln b$, where $z = [1 - \tilde \beta (1 - \gamma ) / (\varepsilon - \gamma )]$. For b>1, the wage rate goes to infinity as $\tilde \beta \to 0$. For b < 1, it goes to zero as $\tilde \beta \to 0$ (as the term in braces is less than one and raised to an increasingly large power) and is monotonically increasing. That is, lower $1 - \tilde \beta$ implies higher wage pressure. To make sure that δ < 1, it thus suffices to assume that b < 1 and $\tilde \beta < \beta$. Since δ is a continuous function of $\tilde \beta$, there exists a lower bound for $\tilde \beta$ above which $\delta \geq \underline \delta$.

Derivation of (18) and Proof that dΔ/d δ < 0 Let $\tilde x^{N}$ denote the output of a firm in an industry with commitment. From Eqs. 3 and 16, $\tilde x^{N} / x^{N} = \delta ^{- \varepsilon }$. Employment in the industry is $\tilde L^{N} = (n - n^{S} - \tilde n^{M}) a^{N} \tilde x^{N}$. Employment in an industry without commitment to wage restraint is L ^N = (n−n ^S−n ^M)a ^N x ^N. So

$$ \frac{\tilde L^{N}}{L^{N}} = \frac{n - n^{S} - \tilde n^{M}}{n - n^{S} - n^{M}} \delta^{- \varepsilon} . $$

(33)

Substitution into

$$\frac{\tilde L^{N}}{\bar L^{N}} \left(\frac{\tilde w^{N}}{P} \right)^{\beta} + \left(1 - \frac{\tilde L^{N}}{\bar L^{N}} \right) b \geq \frac{L^{N}}{\bar L^{N}} \left(\frac{w^{N}}{P} \right)^{\beta} + \left(1 - \frac{L^{N}}{\bar L^{N}} \right) b , $$

using Eqs.7 and 16, and rearranging terms gives (18).

Evaluating Δ at $\underline \delta$ and one yields one and zero, respectively. The derivative of the right-hand side of the inequality in Eq. 18 is

$$\frac{d{\Delta}}{d\delta} = \frac{\delta^{- \varepsilon - 1}}{\beta (1 - \gamma)} \left\{ - \varepsilon \left[ \varepsilon - \gamma - \beta (1 - \gamma) \right] + (\varepsilon - \beta) (\varepsilon - \gamma) \delta^{\beta} \right\} . $$

The term in braces is negative for δ = 1 and increasing in δ. So dΔ/d δ < 0 for all δ ≤ 1.

Proof of Proposition 6

Since (19) is stronger than (10), by Proposition 1, the economy without the possibility of commitment possesses a unique equilibrium ((p ^∗(i, j), x ^∗(i, j)) _{i ∈ [0,1], j ∈ [0, n]}, w ^N∗, w ^S∗, n ^M∗). Consider first equilibria at which no union appoints a PUL, i.e., μ = 0. Suppose

$$ \left((p^{*} (i, j) , x^{*} (i, j))_{i \in [0, 1] , j \in [0 , n]} , w^{N*} , \tilde w^{N} , w^{S*} , n^{M*} , \tilde n^{M} , 0 \right) $$

(34)

is such an equilibrium. Prices and quantities are the same as in the case without the possibility to commit to wage moderation. Since there are no industries with a PUL, $\tilde w^{N}$ and $\tilde n^{M}$ are indeterminate.

The allocation and prices in Eq. 34 in fact constitute an equilibrium if for each given industry, union members’ expected utility does not rise by appointing a PUL. For $f^{M} \geq \bar {f}^{M}$, since there is no offshoring anyway, unions have no incentives to commit to wage restraint. For $f^{M} < \bar {f}^{M}$ and, hence, n ^M∗>0, the operating profit differential is equal to the fixed cost of offshoring without a PUL. It becomes smaller than the cost of offshoring, and there is no offshoring (i.e., $\tilde n^{M} = 0$), with a PUL. So the condition that expected utility does not rise requires that Eq. 18 does not hold with strict inequality for n ^M = n ^M∗ = Φ(f ^M) and $\tilde n^{M} = 0$, i.e.,

$$ \frac{\Phi (f^{M})}{n - n^{S}} \leq {\Delta} . $$

(35)

Since Φ(f ^M) is a continuous function that falls from n−n ^S to zero as f ^M rises from $\underline {f}^{M}$ to $\bar {f}^{M}$ and 0<Δ≤1, there is unique ${f^{M}_{0}} \in (\underline {f}^{M} , \bar {f}^{M})$ such that Eq. 35 holds with equality. The prices and allocation in Eq. 34 are an equilibrium for $f^{M} \geq {f^{M}_{0}}$.

Turning to equilibria with μ = 1, consider the economy without the possibility of commitment and with γ replaced with $\tilde \gamma$ (or, equivalently, b replaced with $\tilde b$), all other parameters held constant. The equilibrium analysis in Section 3 goes through, with the sole modification that ω ^N is replaced with δ ω ^N. Given (19), Proposition 1 states that there exist ${\underline {f}^{M}_{1}}$ and $\underline {\bar L}^{N}_{1}$ such that for $f^{M} > {\underline {f}^{M}_{1}}$ and $\bar L^{N} > \underline {\bar L}^{N}_{1}$, a unique equilibrium ((p ^∗(i, j), x ^∗(i, j)) _{i ∈ [0,1], j ∈ [0, n]}, w ^N∗, w ^S∗, n ^M∗) of this economy exists. Taking the same steps as in the proof of Proposition 1 demonstrates ${\underline {f}^{M}_{1}} < \underline {f}^{M}$. Let ${\bar {f}^{M}_{1}}$ ($< \bar {f}^{M}$) denote the value of f ^M that satisfies (26) with equality when ω ^N is replaced by δ ω ^N. From Proposition 1, n ^M∗>0 for $f^{M} < {\bar {f}^{M}_{1}}$ and n ^M∗ = 0 for $f^{M} \geq \bar {f}{^{M}_{1}}$.

We conjecture that for f ^M sufficiently small,

$$ \left((p^{*} (i, j) , x^{*} (i, j))_{i \in [0, 1] , j \in [0 , n]} , w^{N} , \delta w^{N*} w^{S*} , n^{M} , n^{M*} , 1 \right) $$

(36)

is an equilibrium of the economy with firm bargaining power γ and with the possibility of commitment. That is, all unions install a PUL (i.e., μ = 1), and prices and quantities are the same as in the case when this opportunity does not exist but bargaining power is $\tilde \gamma$. Since there are no industries without a PUL, w ^N and n ^M are indeterminate.

Suppose first $f^{M} < {\bar {f}^{M}_{1}}$, so that n ^M∗>0. The operating profit differential is equal to the fixed cost of offshoring for the economy with firm bargaining power $\tilde \gamma$ and without commitment in this case. Given the prices in Eq. 36, the same holds true for the economy with commitment. If a single union gives up the commitment, all firms offshore: n ^M = n−n ^S. Together with $\tilde n^{M} = n^{M*}$, the condition that it does not pay to give up commitment (18) becomes Δ≤1, which is implied by Eq. 17. So for $f^{M} \in ({\underline {f}^{M}_{1}} , {\bar {f}^{M}_{1}})$, (36) is an equilibrium.

Next, let $f^{M} \geq {\bar {f}^{M}_{1}}$, so that n ^M∗ = 0. (36) is an equilibrium if, and only if, firms offshore production when a union gives up its commitment to wage restraint. Without a PUL the wage rate and the markup price rises by factor δ ⁻¹, demand falls by factor δ ^ε, and operating profit becomes δ ^ε−1 w ^{N ∗} a ^N x ^N∗/(ε−1). Following the same steps as in the derivation of Eq. 6, we obtain the following condition that offshoring becomes profitable:

$$(\varepsilon - 1) f^{M} < \left[ 1 - \delta^{\varepsilon - 1} \left(\frac{w^{N*} a^{N}}{w^{S*} a^{S}} \right)^{1 - \varepsilon} \right] \left(\frac{w^{N*} a^{N}}{w^{S*} a^{S}} \right)^{\varepsilon} a^{S} x^{N*} , $$

where x ^N∗ is the equilibrium output of a Northern firm with a PUL. Using Eqs. 8 and 9 with n ^M = 0 and ω ^N replaced with δ ω ^N, this can be rewritten as

$$ f^{M} < \frac{\alpha^{\varepsilon} \bar L^{S}}{(\varepsilon - 1) n^{S}} \left[ 1 - \delta^{\varepsilon - 1} \frac{n^{S}}{(\delta \omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S})} \right] = {f^{M}_{1}} . $$

(37)

Notice that ${f^{M}_{1}} > {\bar {f}^{M}_{1}}$ because of the additional factor δ ^ε−1.

From Proposition 1, $\bar L^{N} > \underline {\bar L}^{N}$ ensures equilibrium unemployment at Eq. 34, since quantities are the same in the identically parameterized economy without commitment. Let $\underline {\bar L}^{N}_{1}$ be determined analogously for the economy with real wage δ ω ^N/a ^N. Then $\bar L^{N} > \underline {\bar L}^{N}_{1}$ ensures equilibrium unemployment at Eq. 36. □

Equation (20) For $f^{M} = \bar {f}^{M}$, from L ^N = (n−n ^S−n ^M)a ^N x ^N, (8), and (9) with n ^M = 0 and (17), workers’ expected utility is

$$\frac{(n - n^{S}) a^{N} \alpha^{\varepsilon} \bar L^{S} (a^{S})^{\frac{1 - \alpha}{\alpha}} \left(\frac{\omega^{N}}{a^{N}} \right)^{\beta}}{\bar L^{N} a^{S}} \frac{1 - \underline \delta^{\beta}}{\left[ \left(\omega^{N} \right)^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S}) \right]^{\frac{1}{\alpha}}} + b . $$

Using the analogous expression for the case with wage restraint yields expected utility at $f^{M} = \bar {f^{M}_{1}}$. The only differences are that in the latter fraction, the numerator becomes $\delta ^{\beta } - \underline \delta ^{\beta }$ and ω ^N is replaced with δ ω ^N in the denominator. Comparing the two levels of expected utility yields (20).

The derivative of the left-hand side of Eq. 20 is negative exactly if

$$\alpha \beta \delta^{\beta} \left[ \left(\omega^{N} \right)^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S}) \right] < (\varepsilon - 1) \left(\delta \omega^{N} \right)^{\varepsilon - 1} \left(\delta^{\beta} - \underline \delta^{\beta} \right) . $$

Condition (20) is satisfied for δ close enough to one exactly if this inequality holds for δ = 1. Substituting for $\underline \delta$ from Eq. 17 and solving for γ yields the inequality in the main text.

Proof of Proposition 7

Offshoring activity is positive in industries without a PUL (i.e., n ^M>0) at an equilibrium with 0<μ < 1. Otherwise unions with a PUL would have an incentive to dismiss him, since this would not cause offshoring. The fact that the wage rate is lower in industries with a PUL implies $\tilde n^{M} = 0$. Since some unions opt for a PUL and other do not, (18) must hold with equality:

$$ n^{M} = {\Delta} (n - n^{S}) . $$

(38)

As in the baseline model, ignore the condition that there is unemployment to begin with. The price setting equation becomes

$$\begin{array}{@{}rcl@{}} \left(\frac{w^{N} a^{N}}{P} \right)^{\varepsilon - 1} & = & (1 - \mu) \left[ \alpha^{\varepsilon - 1} \left(n - n^{S} - n^{M} \right) + \left(n^{S} + \alpha^{\varepsilon - 1} n^{M} \right) \left(\frac{w^{N} a^{N}}{w^{S} a^{S}} \right)^{\varepsilon - 1} \right] \\ & & + \mu \left[ \left(\frac{\alpha}{\delta} \right)^{\varepsilon - 1} \left(n - n^{S} \right) + n^{S} \left(\frac{w^{N} a^{N}}{w^{S} a^{S}} \right)^{\varepsilon - 1} \right] . \end{array} $$

(39)

n ^M>0 implies that the condition for non-profitability of further offshoring (6) holds with equality for industries without a PUL. The condition for labor market clearing in the South reads

$$ \bar L^{S} = \left[ \alpha^{- \varepsilon} n^{S} + (1 - \mu) n^{M} \right] \left(\frac{w^{N} a^{N}}{w^{S} a^{S}} \right)^{\varepsilon} a^{S} x^{N} + (1 - \mu) n^{M} f^{M} . $$

(40)

Equations 6 (with equality), (7), (38), (39), and (40) determine w ^N/P, n ^M, (w ^N a ^N)/(w ^S a ^S), x ^N, and μ. Equation 16 then pins down $\tilde w^{N} / P$.From Eqs. 7 and 39,

$$ \frac{w^{N} a^{N}}{w^{S} a^{S}} = \left[ \frac{(\omega^{N})^{\varepsilon - 1} - \left(1 - \mu + \frac{\mu}{\delta^{\varepsilon - 1}} \right) \alpha^{\varepsilon - 1} (n - n^{S}) + (1 - \mu) \alpha^{\varepsilon - 1} n^{M}}{n^{S} + (1 - \mu) \alpha^{\varepsilon - 1} n^{M}} \right]^{\frac{1}{\varepsilon - 1}} . $$

(41)

From Eq. 6 (with equality) and Eq. 40,

$$\frac{w^{N} a^{N}}{w^{S} a^{S}} = \left[1 - (\varepsilon - 1) \frac{\alpha^{- \varepsilon} n^{S} + (1 - \mu) n^{M}}{\frac{\bar L^{S}}{f^{M}} - (1 - \mu) n^{M}} \right]^{\frac{1}{1 - \varepsilon}} . $$

Using Eq. 38, it follows that

$$ \frac{n^{S} + (1 - \mu) \alpha^{\varepsilon - 1} {\Delta} (n - n^{S})}{(\omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} \left[(1 - \mu) (1 - {\Delta}) + \frac{\mu}{\delta^{\varepsilon - 1}} \right] (n - n^{S})} = 1 - (\varepsilon - 1) \frac{\alpha^{- \varepsilon} n^{S} + (1 - \mu) {\Delta} (n - n^{S})}{\frac{\bar L^{S}}{f^{M}} - (1 - \mu) {\Delta} (n - n^{S})} . $$

(42)

Denote the left-hand side of Eq. 42 as $\tilde f (\mu ) : [0 , 1] \rightarrow \mathbb {R}_{+}$ and the right-hand side as $\tilde g (\mu , f^{M})$. Condition (38) and the labor market clearing condition for the South (40) jointly imply that the denominator of the fraction on the right-hand side is positive. So $\tilde g$ maps

$$\left\{ (\mu , \, f^{M}) \in [0 , 1] \times (\underline{f}^{M} , \infty) \left| \, \, \frac{\bar L^{S}}{f^{M}} < (1 - \mu) {\Delta} (n - n^{S}) \right. \right\} $$

to $\mathbb {R}$. $\tilde f$ is positive-valued and continuous. $d \tilde f (\mu ) / d\mu$ is positive if

$$(\delta \omega^{N})^{\varepsilon - 1} - \alpha^{\varepsilon - 1} (n - n^{S}) - n^{S} < \frac{(1 - {\Delta}) (1 - \delta^{\varepsilon - 1})}{\Delta} n^{S} $$

and negative when the inequality sign is reversed. $\tilde g (\mu , f^{M})$ is positive for

$$\mu > 1 - \frac{\frac{\bar L^{S}}{f^{M}} - (\varepsilon - 1) \alpha^{- \varepsilon} n^{S}}{\varepsilon {\Delta} (n - n^{S})} . $$

It is continuous and increasing in μ and decreasing in f ^M whenever it is positive. From Eqs. 9, 11, and 38, $\tilde f (0) = \tilde g (0 , f^{M})$ if $f ({\Phi } ({f^{M}_{0}})) = g ({\Phi } ({f^{M}_{0}}) , f^{M})$, i.e., if $f^{M} = {f^{M}_{0}}$. $\tilde f (1) > \tilde g (1 , f^{M})$ exactly if $f^{M} > {f^{M}_{1}}$, where ${f^{M}_{1}}$ is defined in Eq. 37. Since (42) can be rewritten as a quadratic equation in μ, it has at most two solutions μ.

In what follows, we distinguish four cases. In each case, we check the existence of equilibrium as f ^M goes from ${f^{M}_{0}}$ to ${f^{M}_{1}}$.

• Case 1: ${f^{M}_{0}} > {f^{M}_{1}}$, $d \tilde f (0) / d\mu > \partial \tilde g (0 , {f^{M}_{0}}) / \partial \mu$:

Let $f^{M} = {f^{M}_{0}}$, so that $\tilde f (0) = \tilde g (0 , f^{M})$. From the case distinction, $\tilde f (\mu )$ is steeper than $\tilde g (\mu , {f^{M}_{0}})$ at μ = 0 and $\tilde f (1) > \tilde g (1 , {f^{M}_{0}})$. Since $\tilde f$ and $\tilde g$ intersect at most twice, $\tilde f (\mu ) > \tilde g (\mu , {f^{M}_{0}})$ over the entire interval (0,1]. As f ^M falls from ${f^{M}_{0}}$ to ${f^{M}_{1}}$, $\tilde g (\mu , {f^{M}_{0}})$ rises for all μ, so $\tilde f (0) < \tilde g (0 , f^{M})$. Since $\tilde f (1) > \tilde g (1 , f^{M})$ continues to hold, there is unique μ in the unit interval which solves $\tilde f (\mu ) = \tilde g (\mu , f^{M})$, and this μ rises continuously from zero to one (see the upper left panels of Figs. 4 and 6).

• Case 2: ${f^{M}_{0}} > {f^{M}_{1}}$, $d \tilde f (0) / d\mu < \partial \tilde g (0 , {f^{M}_{0}}) / \partial \mu$:

  Fig. 6

  

  Equilibrium with PULs

$\tilde f (\mu )$ is flatter than $\tilde g (\mu , {f^{M}_{0}})$ at μ = 0, and $\tilde f (1) > \tilde g (1 , {f^{M}_{0}})$. Given that $\tilde f$ is monotonic, it must be increasing in this case. There is unique μ in the interval (0,1) such that $\tilde f (\mu ) = \tilde g (\mu , {f^{M}_{0}})$. As f ^M falls from ${f^{M}_{0}}$ to ${f^{M}_{1}}$, this intersection of $\tilde f (\mu ) = \tilde g (\mu , f^{M})$ converges to μ = 1. For f ^M slightly larger than ${f^{M}_{0}}$, an intersection of $\tilde f (\mu )$ and $\tilde g (\mu , f^{M})$ arises at μ close to zero. As f ^M rises further, the two intersections converge to each other (see the upper right panels of Figs. 4 and 6).

• Case 3: ${f^{M}_{0}} < {f^{M}_{1}}$, $d \tilde f (0) / d\mu < \partial \tilde g (0 , {f^{M}_{0}}) / \partial \mu$:

There is a unique intersection of $\tilde f (\mu )$ and $\tilde g (\mu , {f^{M}_{0}})$ in the unit interval (irrespective of whether $\tilde f$ is monotonically increasing or decreasing). For f ^M close to ${f^{M}_{0}}$, the intersection occurs at μ close to zero. As f ^M rises, so does μ. As $f^{M} \to {f^{M}_{1}}$, $\tilde g (1 , f^{M})$ converges to $\tilde f (1)$, so μ goes to unity (see the lower left panels of Figs. 4 and 6).

• Case 4: ${f^{M}_{0}} < {f^{M}_{1}}$, $d \tilde f (0) / d\mu > \partial \tilde g (0 , {f^{M}_{0}}) / \partial \mu$:

$\tilde f (\mu ) = \tilde g (\mu , {f^{M}_{0}})$ for μ = 0 and for some μ in (0,1). As f ^M rises from ${f^{M}_{0}}$ to ${f^{M}_{1}}$, the unique value μ at which $\tilde f (\mu )$ and $\tilde g (\mu , f^{M})$ intersect rises towards one. As f ^M falls below ${f^{M}_{0}}$, there are two intersections, which converge to each other (see the lower right panels of Figs. 4 and 6).

From Eqs. 33, 40, and 41, employment in industries with a PUL is

$$\begin{array}{@{}rcl@{}} \tilde L^{N} & = & (n - n^{S}) \delta^{- \varepsilon} a^{N} \frac{\bar L^{S} - (1 - \mu) n^{M} f^{M}}{a^{S} \left[ \alpha^{- \varepsilon} n^{S} + (1 - \mu) n^{M} \right]} \\ & & \left[ \frac{n^{S} + (1 - \mu) \alpha^{\varepsilon - 1} n^{M}}{(\omega^{N})^{\varepsilon - 1} - \left(1 - \mu + \frac{\mu}{\delta^{\varepsilon - 1}} \right) \alpha^{\varepsilon - 1} (n - n^{S}) + (1 - \mu) \alpha^{\varepsilon - 1} n^{M}} \right]^{\frac{1}{\alpha}} . \end{array} $$

Let $\underline {\tilde L}^{N}$ denote the value of the right-hand side evaluated at n ^M = Δ(n−n ^S) and the equilibrium value of μ. Then there is unemployment in industries with a PUL for $\bar L^{N} > \underline {\tilde L}^{N}$. Since employment is lower in industries without wage restraint, there is also unemployment in these industries. □

Derivation of (21) and (22) From the pricing rules,

$$\left(\frac{w^{N} a^{N}}{\alpha P} \right)^{\varepsilon - 1} = n - \left[ 1 - \left(\frac{w^{N} a^{N}}{w^{S} a^{S}} \right)^{\varepsilon - 1} \right] n^{M} . $$

The fixed cost of setting up a subsidiary is v ^N f ^N+w ^S f ^M. This is equal to the operating profit differential if

$$(\varepsilon - 1) \left(\frac{v^{N}}{w^{S}} f^{N} + f^{M} \right) = \left[ 1 - \left(\frac{w^{N} a^{N}}{w^{S} a^{S}} \right)^{1 - \varepsilon} \right] \left(\frac{w^{N} a^{N}}{w^{S} a^{S}} \right)^{\varepsilon} a^{S} x^{N} . $$

As before, the wage bargain gives rise to the RTM wage w ^N/P = ω ^N/a ^N. Labor market clearing in the South requires

$$\bar L^{S} = n^{M} \left[ \left(\frac{w^{N} a^{N}}{w^{S} a^{S}} \right)^{\varepsilon} a^{S} x^{N} + f^{M} \right] . $$

Eliminating x ^N, w ^N/P, and v ^N from these equations, the market clearing condition for skilled labor, and the free entry condition yields (21) and (22). Define $\hat f$ and $\hat g$ as the functions on the right-hand sides of Eqs. 21 and 22, respectively. $\hat f$ and $\hat g$ map $\{ \mathbb {R}_{+} \backslash \{ 0 \} \}$ and

$$\left\{ (n^{M} , \, f^{M}) \in \mathbb{R}^{2}_{+} \left| \, \, n^{M} < \frac{\bar L^{S}}{\varepsilon f^{M}} \right. \right\} , $$

respectively, on the positive reals. Both functions are continuous.

Proof of Proposition 8

Given (23), $\hat f (n^{M})$ falls from infinity to (1+f ^N/f ^I)^1/(ε−1) as n ^M rises from zero to infinity. $\hat g (n^{M} , f^{M})$ rises from (1+f ^N/f ^I)^1/(ε−1) to infinity as n ^M rises from zero to $\bar L^{S} / (\varepsilon f^{M})$. So there is a unique solution to Eqs. 21 and 22.

The value of n ^M determined by Eqs. 21 and 22 is a continuous decreasing function of f ^M. Evidently, from Eqs. 21 and 22, it goes to infinity as f ^M→0. Let $\underline {f}^{M}$ denote the value of f ^M such that $n^{M} = \bar H^{N} / (f^{N} + f^{I})$. From the market clearing condition for skilled labor, n ^M≤n exactly if $n^{M} \leq \bar H^{N} / (f^{N} + f^{I})$. Note also that, as f ^M goes to infinity, n ^M ($< \bar L^{S} / (\varepsilon f^{M})$) goes to zero.

From the labor market clearing condition for the South and (21), equilibrium employment of unskilled labor in the North can be written as

$$L^{N} = (n - n^{M}) \frac{a^{N}}{a^{S}} \left(\frac{\bar L^{S}}{n^{M}} - f^{M} \right) \left\{ \frac{1}{n^{M}} \left[ \left(\frac{\omega^{N}}{\alpha} \right)^{\varepsilon - 1} - \frac{\bar H^{N}}{f^{I}} \right] + \left(1 + \frac{f^{N}}{f^{I}} \right) \right\}^{- \frac{\varepsilon}{\varepsilon - 1}} . $$

L ^N goes to zero as $f^{M} \to \underline {f}^{M}$ (so that n ^M→n). L ^N also goes to zero as $f^{M} \to \infty$. This follows from n ^M→0 and

$$L^{N} < (n - n^{M}) \frac{a^{N}}{a^{S}} \bar L^{S} \left[ \left(\frac{\omega^{N}}{\alpha} \right)^{\varepsilon - 1} - \frac{\bar H^{N}}{f^{I}} \right]^{- \frac{\varepsilon}{\varepsilon - 1}} (n^{M})^{\frac{1}{\varepsilon - 1}} . $$

□

Appendix B: Numerical example

This Appendix provides a numerical example which illustrates results such as hump-shaped employment and multiplicity of equilibria with PULs.

The model parameters are summarized in Table 1. Workers’ risk aversion is low (β is large). The value for firms’ bargaining power γ is in the range covered by DuMont et al.’s (2006, 2012) estimates. Labor in the South is half as productive as labor in the North. Commitment to wage restraint entails a ten-percent wage cut compared to the RTM wage.

Table 1 Model parameters

Without commitment to wage restraint, the measure of varieties per industry produced in MNEs in the South rises from zero to (n−n ^S = ) 9 as the labor requirement for offshoring falls from ($\bar {f}^{M} =$) 1.467 to ($\underline {f}^{M} =$) 0.167 (see the left panel of Fig. 7). Employment in the North rises by (0.707/0.639−1=) 10.6 percent as f ^M falls from 1.467 to f ^M = 0.824 and then starts to fall (see the right panel of Fig. 7). It is back at its level without offshoring when f ^M = 0.497, i.e., 33.9 percent of the level at which offshoring becomes profitable. Hence, high unemployment due to intensive offshoring occurs only for very low levels of the cost of offshoring.

Fig. 7

Equilibrium without PULs

When unions have the opportunity to commit to a ten-percent wage cut, an equilibrium at which no union commits to wage restraint exists for f ^M>0.958, and an equilibrium with PULs in all industries exists for f ^M<1.385. For f ^M-values in between, there also exists an equilibrium with commitment in some but not all industries (see the left panel of Fig. 8). The equilibrium measure of MNEs per industry with offshoring activity n ^M is illustrated in the middle panel of Fig. 8. Aggregate employment attains its maximum 1.103 at f ^M = 0.863. For f ^M in the vicinity of this value, employment is higher than at an equilibrium with no offshoring but no wage restraint either, as the threat of offshoring induces wage restraint.

Fig. 8

Equilibrium with PULs