Integrated likelihoods in parametric survival models for highly clustered censored data

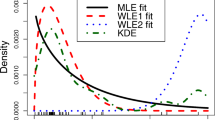
Abstract

In studies that involve censored time-to-event data, stratification is frequently encountered due to different reasons, such as stratified sampling or model adjustment due to violation of model assumptions. Often, the main interest is not in the clustering variables, and the cluster-related parameters are treated as nuisance. When inference is about a parameter of interest in presence of many nuisance parameters, standard likelihood methods often perform very poorly and may lead to severe bias. This problem is particularly evident in models for clustered data with cluster-specific nuisance parameters, when the number of clusters is relatively high with respect to the within-cluster size. However, it is still unclear how the presence of censoring would affect this issue. We consider clustered failure time data with independent censoring, and propose frequentist inference based on an integrated likelihood. We then apply the proposed approach to a stratified Weibull model. Simulation studies show that appropriately defined integrated likelihoods provide very accurate inferential results in all circumstances, such as for highly clustered data or heavy censoring, even in extreme settings where standard likelihood procedures lead to strongly misleading results. We show that the proposed method performs generally as well as the frailty model, but it is superior when the frailty distribution is seriously misspecified. An application, which concerns treatments for a frequent disease in late-stage HIV-infected people, illustrates the proposed inferential method in Weibull regression models, and compares different inferential conclusions from alternative methods.

Appendix

1.1 Expected score for the ith cluster

In the following, we prove that the expected score for the ith cluster has the form given in (8).

Let us consider, for $i=1,\ldots ,n$, the score functions for the nuisance parameters reported in Eq. (7). We need now to compute the expected score of $\ell ^i_{\lambda _i} (\psi , \lambda _i)$ with respect to the processes in the true parameter $(\psi _0, \lambda _{i0})$. For this purpose, we proceed as follows.

For the leading integral on the right-hand side of (7), we use the Doob-Meyer decomposition $dN_{ij}(t) = h_{ij}(t; \psi _0, \lambda _{i0}) \, Y_{ij}(t) \,dt + dM_{ij}(t)$, where $h_{ij}(t; \psi _0, \lambda _{i0}) \, Y_{ij}(t) dt$ is a unique predictable process and $dM_{ij}(t)$ is a martingale increment. Therefore, we obtain

$$\begin{aligned}&E \left\{ \ell ^i_{\lambda _i} (\psi , \lambda _i); \psi _0, \lambda _{i0} \right\} \\&= \sum _{j=1}^k E \left\{ \left( \int _0^{\infty } \frac{\partial }{\partial \lambda _i} \log h_{ij} (t; \psi , \lambda _i) \, h_{ij}(t; \psi _0, \lambda _{i0}) \, Y_{ij}(t) \, dt \right. \right. \\&\qquad \qquad \qquad + \int _0^{\infty } \frac{\partial }{\partial \lambda _i} \log h_{ij} (t ; \psi , \lambda _i) \,dM_{ij}(t) \\&\qquad \qquad \qquad \left. \left. - \int _0^{\infty } \frac{\partial }{\partial \lambda _i} h_{ij} (t ; \psi , \lambda _i)~ Y_{ij}(t) \,dt \right) ; \psi _0, \lambda _{i0} \right\} . \end{aligned}$$

The second integral on the right-hand side is a stochastic integral with respect to a martingale, and is itself also a martingale, since its integrand is a bounded predictable process. Therefore, the expected value of this integral is equal to zero. Consider now the expected values of the remaining two integrals with respect to the process $h_{ij}(t; \psi _0, \lambda _{i0}) \, Y_{ij}(t)$; interchanges of integrals follow from Fubini’s theorem and we obtain the following general expression for the expected score of the ith cluster:

$$\begin{aligned}&E \left\{ \ell _{\lambda _i}^i (\psi , \lambda _i); \psi _0, \lambda _{i0} \right\} \nonumber \\&\quad = \sum _{j=1}^k \left\{ \int _0^{\infty } \frac{\partial }{\partial \lambda _i} \log h_{ij} (t ; \psi , \lambda _i) \, h_{ij} (t ; \psi _0, \lambda _{i0}) \, y_{ij}(t; \psi _0, \lambda _{i0})\, dt \right. \nonumber \\&\qquad \qquad \quad \left. - \int _0^{\infty } \frac{\partial }{\partial \lambda _i} h_{ij} (t ; \psi , \lambda _i) \, y_{ij} (t ; \psi _0, \lambda _{i0}) \, dt \right\} , \end{aligned}$$

(21)

where $y_{ij}(t; \psi _0, \lambda _{i0}) = E\left\{ Y_{ij}(t); \psi _0, \lambda _{i0} \right\}$. Rewriting this expression with $\frac{\partial }{\partial \lambda _i} \log h_{ij} (t ; \psi , \lambda _i) = \frac{\partial }{\partial \lambda _i} h_{ij} (t ; \psi , \lambda _i) / h_{ij} (t ; \psi , \lambda _i)$ gives the final equation in (8).

1.2 Expected score for the ith cluster under type I censoring

We show here the derivations of the expected score equation for the ith cluster given in (10).

Under type I censoring, let us assume that the censoring times for each cluster are constant, i.e., $c_{i1}=\ldots = c_{ik}=c_i$ for $i=1,\ldots ,n$. Then, we have $y_{ij}(t; \psi _0, \lambda _{i0}) = S_{ij} (t; \psi _0, \lambda _{i0})$ for $t \le c_i$, and $y_{ij}(t; \psi _0, \lambda _{i0}) = 0$ for $t > c_i$. By inserting these expression in the expected score Eq. (21), together with $h_{ij}(t)= p_{ij}(t) / S_{ij}(t)$, it follows that

$$\begin{aligned} E \left\{ \ell _{\lambda _i}^i (\psi , \lambda _i); \psi _0, \lambda _{i0} \right\}= & {} \sum _{j=1}^k \left\{ \int _0^{c_i} \frac{\partial }{\partial \lambda _i} \log p_{ij} (t ; \psi , \lambda _i) ~ p_{ij} (t ; \psi _0, \lambda _{i0}) \, dt \right. \\&\qquad \quad - \int _0^{c_i} \frac{\partial }{\partial \lambda _i} \log S_{ij} (t ; \psi , \lambda _i) ~ p_{ij} (t ; \psi _0, \lambda _{i0}) \, dt \\&\qquad \quad \left. - \int _0^{c_i} \frac{\partial }{\partial \lambda _i} h_{ij} (t ; \psi , \lambda _i) ~ S_{ij} (t ; \psi _0, \lambda _{i0}) \, dt \right\} . \end{aligned}$$

Observe that if $g'(t) = \frac{\partial }{\partial \lambda _i} h_{ij} (t ; \psi , \lambda _i) = \frac{\partial }{\partial \lambda _i} \left( - \frac{d}{dt} \log S_{ij}(t; \psi , \lambda _i) \right) = - \frac{d}{dt} \left( \frac{\partial }{\partial \lambda _i} \log S_{ij}(t; \psi , \lambda _i) \right)$, then $g(t)= - \frac{\partial }{\partial \lambda _i} \log S_{ij} (t; \psi , \lambda _i)$. Therefore, by using this fact and integration by parts for the third integral on the right-hand side, we have

$$\begin{aligned} \begin{aligned} \int _0^{c_i} \frac{\partial }{\partial \lambda _i} h_{ij} (t ; \psi , \lambda _i) ~ S_{ij} (t ; \psi _0, \lambda _{i0}) \, dt =&- \frac{\partial }{\partial \lambda _i} \log S_{ij} (c_i ; \psi , \lambda _i) ~ S_{ij} (c_i ; \psi _0, \lambda _{i0}) \\&- \int _0^{c_i} \frac{\partial }{\partial \lambda _i} S_{ij} (t ; \psi , \lambda _i) ~ p_{ij} (t ; \psi _0, \lambda _{i0}) \, dt. \\ \end{aligned} \end{aligned}$$

Using this result for the third integral on the right-hand side of the expected score, we obtain

$$\begin{aligned} \begin{aligned} E \left\{ \ell _{\lambda _i}^i (\psi , \lambda _i); \psi _0, \lambda _{i0} \right\} = \sum _{j=1}^k&\left\{ \int _0^{c_i} \frac{\partial }{\partial \lambda _i} \log p_{ij} (t ; \psi , \lambda _i) ~ p_{ij} (t ; \psi _0, \lambda _{i0}) \, dt \right. \\&\quad \left. +\, \frac{\partial }{\partial \lambda _i} \log S_{ij} (c_i ; \psi , \lambda _i) ~ S_{ij} (c_i ; \psi _0, \lambda _{i0}) \right\} . \end{aligned} \end{aligned}$$

Finally, Eq. (10) follows by changing the notation to $\eta _{ij} (t; \psi , \lambda _i) = \frac{\partial }{\partial \lambda _i} \log p_{ij}(t;\psi , \lambda _i),$ and $H_{ij} (t; \psi , \lambda _i) = \frac{\partial }{\partial \lambda _i} log S_{ij}(t;\psi , \lambda _i)$, and setting the expected score equal to zero.

1.3 Integrated likelihood for the Weibull regression model

For the regression model (19), the expected score for the nuisance $\alpha _i$ is given by

$$\begin{aligned} E\{ \ell ^i_{\alpha _i} (\psi _1,\psi _2,\alpha _i); \hat{\psi }_1, \hat{\psi }_2, \omega _i \} = \sum _j \left( \frac{\partial \eta _{ij}}{\partial \alpha _i} \right) E \left\{ \ell _{\eta _{ij}}^i (\psi _1, \eta _{ij}); \hat{\psi }_1, \phi _{ij} \right\} . \end{aligned}$$

(22)

An explicit expression can be obtained by applying the theory in Sect. 4 to a Weibull$(\eta _{ij}, \psi _1)$. Thus, $\eta _{ij}, \psi _1$ and $\phi _{ij}$ play here the same role as, respectively, $\lambda _i, \psi$ and $\phi _i$ in Sect. 4, with the exception that they depend on the index j because of the presence of covariates. Therefore, we can get $E \{ \ell _{\eta _{ij}}^i (\psi _1, \eta _{ij}); \hat{\psi }_1, \phi _{ij} \}$ by replacing $\lambda _i, \psi$ and $\phi _i$ with $\eta _{ij}, \psi _1$ and $\phi _{ij}$ in expression (15). Then, given that $\partial \eta _{ij} / \partial \alpha _i=-\eta _{ij}$ and using the parameterizations in (20), we can find a final expression for (22).

Setting (22) equal to zero leads to the relation between $\alpha _i$ and the ZSE parameter $\omega _i$, i.e.,

$$\begin{aligned} \alpha _i = -\frac{1}{\psi _1} \log \left[ \frac{\hat{\psi }_1 \sum _j e^{-\hat{\psi }_1 (\omega _i + \hat{\psi }_2 x_{ij})} \int _0^{\infty } t^{\hat{\psi }_1 -1} y_{ij}(t; \hat{\psi }_1,\hat{\psi }_2,\omega _i) dt }{\psi _1 \sum _j e^{-\psi _1 (\alpha _i + \psi _2 x_{ij})} \int _0^{\infty } t^{\psi _1 -1} y_{ij}(t; \hat{\psi }_1,\hat{\psi }_2,\omega _i) dt } \right] . \end{aligned}$$

This equation can also be obtained directly by replacing $\lambda _i, \psi$ and $\phi _i$ with $\eta _{ij}, \psi _1$ and $\phi _{ij}$ in (16).