Identifiability of PBPK models with applications to dimethylarsinic acid exposure

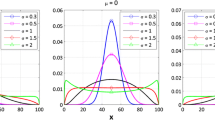
Abstract

Any statistical model should be identifiable in order for estimates and tests using it to be meaningful. We consider statistical analysis of physiologically-based pharmacokinetic (PBPK) models in which parameters cannot be estimated precisely from available data, and discuss different types of identifiability that occur in PBPK models and give reasons why they occur. We particularly focus on how the mathematical structure of a PBPK model and lack of appropriate data can lead to statistical models in which it is impossible to estimate at least some parameters precisely. Methods are reviewed which can determine whether a purely linear PBPK model is globally identifiable. We propose a theorem which determines when identifiability at a set of finite and specific values of the mathematical PBPK model (global discete identifiability) implies identifiability of the statistical model. However, we are unable to establish conditions that imply global discrete identifiability, and conclude that the only safe approach to analysis of PBPK models involves Bayesian analysis with truncated priors. Finally, computational issues regarding posterior simulations of PBPK models are discussed. The methodology is very general and can be applied to numerous PBPK models which can be expressed as linear time-invariant systems. A real data set of a PBPK model for exposure to dimethyl arsinic acid (DMA(V)) is presented to illustrate the proposed methodology.

Appendix

Notation used in this appendix is summarized in Tables 3, 4, 5, and 6.

Table 3 Notation used in mathematical representation of PBPK model of DMA

Table 4 Subscript notation used in mathematical representation of PBPK model of DMA

Table 5 Physiological allometric relationships used in PBPK model of DMA

Mathematical representation of PBPK model of DMA

$$\begin{aligned} \frac{d A_{lun.b} }{d t }&= Q_{lun}(C_{ven.p} - C_{lun.b} ) \\ & \quad -{D_{lun}} Q_{lun} \left( C_{lun.b} - \frac{C_{lun.t} }{{P_{lun}}} \right) \\ \frac{d A_{lun.t} }{d t }&= {D_{lun}} Q_{lun} \left( C_{lun.b} - \frac{C_{lun.t} }{{P_{lun}}} \right) \\ \frac{d A_{art.p} }{d t }&= Q_{lun} \left( C_{lun.b} - C_{art.p} \right) - \\ & \quad {D_{rbc}} Q_{lun} \left( C_{art.p} - \frac{C_{art.rbc} }{{P_{rbc}}} \right) \\ \frac{d A_{art.rbc} }{d t }&= {D_{rbc}} Q_{lun} \left( C_{art.p} - \frac{C_{art.rbc} }{{P_{rbc}}} \right) \\ \frac{d A_{ski} }{d t }&= Q_{ski} \left( C_{art.p} - \frac{C_{ski} }{P_{ski}} \right) \\ \frac{d A_{bla} }{d t }&= Q_{bla} \left( C_{art.p} - \frac{C_{bla} }{P_{bla}} \right) \\ \frac{d A_{res} }{d t }&= Q_{res} \left( C_{art.p} - \frac{C_{res} }{P_{res}} \right) \\ \frac{d A_{kid.b} }{d t }&= Q_{kid}(C_{art.p} - C_{kid.b} ) - \\ & \quad {D_{kid}} Q_{kid} \left( C_{kid.b} - \frac{C_{kid.t} }{{P_{kid}}} \right) \\ \frac{d A_{kid.t} }{d t }&= {D_{kid}} Q_{kid} \left( C_{kid.b} - \frac{C_{kid.t} }{{P_{kid}}} \right) - {k_r} \frac{A_{kid.t} }{{P_{kid}}} \\ \frac{d A_{uri} }{d t }&= {k_r} \frac{A_{kid.t} }{{P_{kid}}} \\ \frac{d A_{sto}}{d t }&= - {k_a} A_{sto} \\ \frac{d A_{liv.b} }{d t }&= Q_{liv}(C_{art.p} - C_{liv.b} ) - \\ & \quad {D_{liv}} Q_{liv} \left( C_{liv.b} - \frac{C_{liv.t} }{{P_{liv}}} \right) + {k_a} A_{sto}\\ \frac{d A_{liv.t} }{d t }&= {D_{liv}} Q_{liv} \left( C_{liv.b} - \frac{C_{liv.t} }{{P_{liv}}} \right) - {k_{m}} A_{liv.t} - {k_b} A_{liv.t}\\ \frac{d A_{met} }{d t }&= {k_{m}} A_{liv.t} \\ \frac{d A_{bil} }{d t }&= {k_{b}} A_{liv.t} \\ \frac{d A_{ven.p} }{d t }&= Q_{ski} \frac{C_{ski} }{P_{ski}} + Q_{bla} \frac{C_{bla}}{P_{bla}} + Q_{res} \frac{C_{res} }{P_{res}} + Q_{kid} C_{kid.b} + \\ & \quad Q_{liv} C_{liv.b} - Q_{lun} C_{ven.p} - \\ & \quad {D _{rbc}} Q_{lun} \left( C_{ven.p} - \frac{C_{ven.rbc} }{{P_{rbc}}} \right) \\ \frac{d A_{ven.rbc} }{d t }&= {D _{rbc}} Q_{lun} \left( C_{ven.p} - \frac{C_{ven.rbc} }{{P_{rbc}}} \right) \\ \end{aligned}$$

Unknown parameters are D _kid , D _liv , D _lun , D _rbc , k _a , k _b , k _r , P _kid , P _liv , P _lun , P _rbc .

PBPK models of DMA expressed as a LTIS

Let

$$\begin{aligned} \varvec{g}= & \quad (A_{lun.b},A_{lun.t},A_{art.p},A_{art.rbc},A_{ski},A_{bla},A_{res}, A_{kid.b},A_{kid.t}, \\ & A_{uri},A_{sto},A_{liv.b},A_{liv.t},A_{met},A_{bil},A_{ven.p},A_{ven.rbc})' \\ \end{aligned}$$

represent the amount of DMA in the compartments of mouse i.

The matrix $\varvec{A}$ is defined as,

$$\begin{aligned} \varvec{A}(\varvec{\delta },\varvec{x}) = [ \varvec{A}_1(\varvec{\delta },\varvec{x}) \; \varvec{A}_2(\varvec{\delta },\varvec{x}) \; \varvec{A}_3(\varvec{\delta },\varvec{x}) ] \end{aligned}$$

where

$$\begin{aligned} & \varvec{A}_1(\varvec{\delta },\varvec{x})= \\ &\left( \quad\begin{array}{llllll} - \frac{( 1 + D_{lun}) Q_{lun} }{V_{lun.b}} &\quad \frac{D_{lun} Q_{lun}}{P_{lun} V_{lun.t}} &\quad 0&\quad 0&\quad 0&\quad 0 \\ \frac{D_{lun} Q_{lun} }{V_{lun.b}} &\quad -\frac{D_{lun} Q_{lun}}{P_{lun} V_{lun.t}} &\quad 0&\quad 0&\quad 0&\quad 0\\ \frac{Q_{lun}}{V_{lun.b}}&\quad 0 &\quad -\frac{(1+D_{rbc}) Q_{lun}}{V_{art.p}} & \quad \frac{D_{rbc} Q_{lun}}{P_{rbc} V_{art.rbc}} & \quad 0&\quad 0\\ 0&\quad 0 &\quad \frac{D_{rbc}Q_{lun}}{V_{art.p}}&\quad -\frac{D_{rbc}Q_{lun}}{P_{rbc} V_{art.rbc}}&\quad 0&\quad 0\\ 0&\quad 0 &\quad \frac{Q_{ski}}{V_{art.p}}&\quad 0&\quad -\frac{Q_{ski}}{P_{ski}V_{ski}}&\quad 0\\ 0&\quad 0 &\quad \frac{Q_{bla}}{V_{art.p}}&\quad 0&\quad 0&\quad -\frac{Q_{bla}}{P_{bla}V_{bla}}\\ 0&\quad 0 &\quad \frac{Q_{res}}{V_{art.p}}&\quad 0&\quad 0&\quad 0\\ 0&\quad 0 &\quad \frac{Q_{kid}}{V_{art.p}}&\quad 0&\quad 0&\quad 0\\ 0&\quad 0 &\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0 &\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0 &\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0 &\quad \frac{Q_{liv}}{V_{art.p}}&\quad 0&\quad 0&\quad 0\\ 0&\quad 0 &\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0 &\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0 &\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0 &\quad 0&\quad 0&\quad \frac{Q_{ski}}{P_{ski} V_{ski} } &\quad \frac{Q_{bla}}{P_{bla} V_{bla} } \\ 0&\quad 0 &\quad 0&\quad 0&\quad 0&\quad 0\\ \end{array}\right)\\ \end{aligned}$$

$$\begin{aligned}&\varvec{A}_2(\varvec{\delta },\varvec{x}) =\\ &\left( \quad\begin{array}{llllll} 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ -\frac{Q_{res}}{ P_{res} V_{res} }&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad -\frac{( 1 + D_{kid} )Q_{kid} }{ V_{kid.b} } &\quad \frac{D_{kid} Q_{kid} }{ P_{kid} V_{kid.t} }&\quad 0&\quad 0&\quad 0\\ 0&\quad \frac{D_{kid} Q_{kid} }{ V_{kid.b} }&\quad -\frac{D_{kid} Q_{kid} }{ P_{kid} V_{kid.t} } - \frac{k_r}{P_{kid}} &\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad \frac{k_r}{P_{kid}}&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad -k_a&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad k_a&\quad -\frac{(1+D_{liv})Q_{liv}}{V_{liv.b}}\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad \frac{D_{liv}Q_{liv}}{V_{liv.b}}\\ 0&\quad 0&\quad 0&\quad 0&\quad 0 & \quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0&\quad 0\\ \frac{Q_{res}}{ P_{res} V_{res} }&\quad \frac{Q_{kid}}{V_{kid.b}} & \quad 0&\quad 0&\quad 0&\quad \frac{Q_{liv}}{V_{liv.b}}\\ 0&\quad 0 & \quad 0&\quad 0&\quad 0&\quad 0\\ \end{array}\right) \end{aligned}$$

and,

$$\begin{aligned} \varvec{A}_3(\varvec{\delta },\varvec{x}) = \left( \begin{array}{llllll} 0&\quad 0&\quad 0&\quad \frac{Q_{lun} }{V_{ven.p}} &\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 0\\ \frac{D_{liv} Q_{liv}}{P_{liv} V_{liv.t} }&\quad 0&\quad 0&\quad 0&\quad 0\\ -\frac{D_{liv} Q_{liv}}{P_{liv} V_{liv.t}} -k_m -k_b &\quad 0&\quad 0&\quad 0&\quad 0\\ k_m&\quad 0&\quad 0&\quad 0&\quad 0\\ k_b&\quad 0&\quad 0&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad -\frac{(1+D_{rbc})Q_{lun}}{V_{ven.p}} &\quad \frac{D_{rbc}Q_{lun}}{P_{rbc} V_{ven.rbc}}\\ 0&\quad 0&\quad 0&\quad \frac{D_{rbc}Q_{lun}}{V_{ven.p}}&\quad -\frac{D_{rbc}Q_{lun}}{P_{rbc} V_{ven.rbc}}\\ \end{array} \right) \end{aligned}$$

where we excluded the dependence on i in the elements in $\varvec{A}_1$, $\varvec{A}_2$ and $\varvec{A}_3$.

For mice which were exposed intravenously to DMA

$$\begin{aligned} \varvec{B}(\varvec{\delta },\varvec{x})&= ( 0 \;0 \;0 \;0 \;0 \;0 \;0 \;0 \;0 \;0 \;0 \;0 \;0 \;0 \;0 \; \text{DR}_{IV} \; \text{C}_{IV,i} \;0)' \\ \varvec{u}(t)&= 1_{[0,t_0]}(t) \\ \varvec{g}_0(\varvec{\delta },\varvec{x})&= {\bf{0}} \end{aligned}$$

where $\text{DR}_{IV}$, $t_0$, and $\text{C}_{IV,i}$ denote the infusion dosing rate, infusion duration, and infusion DMA exposure concentration of mouse i respectively. For these mice, the total DMA exposure is $\text{DR}_{IV} \times t_0 \times \text{C}_{IV,i}$. This amount equals the sums of the amounts of DMA in all of the compartments of mouse i, i.e. $\text{DR}_{IV} \times t_0 \times \text{C}_{IV,i} = {\bf{1}}_{17}' \varvec{g}(t,\varvec{\delta }_i,\varvec{x}_i)$.

For mice which were exposed through oral gavage

$$\begin{aligned} \varvec{B}(\varvec{\delta },\varvec{x})&= {\bf{0}} \\ \varvec{u}(t)&= 0 \\ \varvec{g}_0(\varvec{\delta },\varvec{x})&= \text{F}_{a} \text{V}_{w,i} \text{C}_{w,i} \end{aligned}$$

where $\text{F}_{a}$, $\text{V}_{w,i}$, and $\text{C}_{w,i}$ denote the fraction of DMA absorbed in the gut, water volume exposure and the oral DMA exposure concentration of mouse i respectively. For these mice, the total DMA exposure is $\text{F}_{a} \times \text{V}_{w,i} \times \text{C}_{w,i}$. This amount equals the sums of the amounts of DMA in all of the compartments of mouse i, i.e. $\text{F}_{a} \times \text{V}_{w,i} \times \text{C}_{w,i} = {\bf{1}}_{17}' \varvec{g}(t,\varvec{\delta }_i,\varvec{x}_i)$.

The rows of $\varvec{C}(\varvec{\delta },\varvec{x})$ are reflected in the columns of Table 6. In this table, $V_{s} = V_{s.b} + V_{s.t}$ for s = lun, kid, liv. The elements of each column correspond to the weights of the linear combinations of the state variables. Each column corresponds to one of the seven compartments which was measured.

Since the PBPK model of each mouse is different, the models vary due to differences in the values of the PBPK model parameters, covariates, and exposure conditions. In addition, the models differ in structure because of the different types of exposure and measured compartments. The $\varvec{A}$, $\varvec{B}$ and $\varvec{C}$ matrices are different for each mouse. For example, each column of Table 6 would correspond to a row of $\varvec{C}(\varvec{\delta }_i,\varvec{x}_i)$ if mouse i had that compartment measured. These differences lead to completely different output functions. Thus, two mice which have identical PBPK model parameter values but were exposed differently or had different compartments measured will have completely different output functions.

Table 6 Measured compartments as linear combinations of the state variables of the PBPK model of DMA

Recognizable full conditionals of PBPK models of DMA

The full conditional distribution of the parameters $\varvec{\sigma }^2$, $\varvec{\eta }$, and $\varvec{D}$ are

$$\begin{aligned}\left [ \sigma _k^{-2} | \varvec{Y}, \varvec{\theta }, \varvec{\eta },\varvec{D}, \sigma ^2_l , l \ne k \right ]= \quad& \varvec{G}\left( \alpha _k + (1/2) \sum _{i=1}^{176} \sum _{j \in \varvec{J}_{ik}}, \tilde{\beta }_k \right) \\ \left[ \varvec{\eta }| \varvec{Y}, \varvec{\theta }, \varvec{D}, \sigma _1^2, \ldots ,\sigma _7^2 \right]=\quad & \varvec{{\mathcal {N}}}(\varvec{\eta },\tilde{\varvec{\eta }}_0 \tilde{\varvec{M}},\tilde{\varvec{M}}) \\ \left[ \varvec{D}^{-1} | \varvec{Y}, \varvec{\theta }, \varvec{\eta }, \sigma ^2_1 , \ldots \sigma ^2_7 \right]=\quad & \varvec{W}_{11} \left( \rho + 176, \tilde{\varvec{D}}_0 \right) \end{aligned}$$

where

$$\begin{aligned} \tilde{\beta }_k= \quad& \beta _k + \frac{1}{2} \sum _{i=1}^{176} \sum _{j \in \varvec{J}_{ik}} \left( \log Y_{ijk} - \log f_k(t_{ij},\varvec{E}_i,\varvec{\phi }_i, \varvec{\theta }_i ) \right) ^2 \\ \tilde{\varvec{\eta }}_0= \quad& \varvec{D}^{-1} \sum _{i=1}^{176} \log \varvec{\theta }_i + \varvec{M}^{-1} \varvec{\eta }_0 \\ \tilde{\varvec{M}}= \quad & (176 \varvec{D}^{-1} + \varvec{M}^{-1})^{-1} \\ \tilde{\varvec{D}}_0= & \left( \sum _{i=1}^{176} ( \log \varvec{\theta }_i - \varvec{\eta }) ( \log \varvec{\theta }_i - \varvec{\eta })' + \rho \varvec{D}_0 \right) ^{-1} \end{aligned}$$

The density of the PBPK model parameters of mouse i, $\varvec{\theta }_i$, is not recognizable but is proportional to,

$$\begin{aligned} { \left[ \log \varvec{\theta }_i | \varvec{Y}, \varvec{\eta },\varvec{D}, \sigma _1^2 \ldots \sigma _7^2, \varvec{\theta }_l, l \ne i \right] } \\= \quad & \exp \left( - \sum _{i=1}^{176} \sum _{k=1}^7 \sum _{j \in \varvec{J}_{ik} } \frac{1}{2 \sigma _k^2} \left( \log Y_{ijk} - \log f_k(t_{ij},\varvec{E}_i,\varvec{\phi }_i, \varvec{\theta }_i ) \right) ^2 \right) \\ & \times \exp \left( - \frac{1}{2} ( \log \varvec{\theta }_i - \varvec{\eta }) \varvec{D}^{-1} ( \log \varvec{\theta }_i - \varvec{\eta }) \right) \times 1_{[ \varvec{\theta }_i \in (\varvec{\theta }_l,\varvec{\theta }_u)]} . \end{aligned}$$