Closed form solutions and dominant elimination pathways of simultaneous first-order and Michaelis–Menten kinetics

Abstract

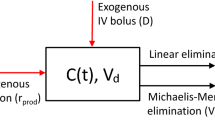
The current study aims to provide the closed form solutions of one-compartment open models exhibiting simultaneous linear and nonlinear Michaelis–Menten elimination kinetics for single- and multiple-dose intravenous bolus administrations. It can be shown that the elimination half-time ($t_{1/2}$) has a dose-dependent property and is upper-bounded by $t_{1/2}$ of the first-order elimination model. We further analytically distinguish the dominant role of different elimination pathways in terms of model parameters. Moreover, for the case of multiple-dose intravenous bolus administration, the existence and local stability of the periodic solution at steady state are established. The closed form solutions of the models are obtained through a newly introduced function motivated by the Lambert W function.

Appendices

Appendix A

Definition 2

For given parameters $v\in (0,1)$, $a\in (0,\infty )$ and $b\in (0,\infty )$, let us define $Y(t,v,a,b)$ as the inverse function of $\displaystyle h(s)=\left( \frac{s}{s+a}\right) ^{1-v}\left( \frac{s+b}{s+a+b}\right) ^v$, for $s>0$, which means

$$\begin{aligned} h(Y(t,v,a,b))=t. \end{aligned}$$

(39)

For any given $v\in (0,1)$, $a\in (0,\infty )$ and $b\in (0,\infty )$, the derivative of $h(s)$ is

$$\begin{aligned} h'(s)=h(s)\biggl [\frac{a(1-v)}{s(s+a)}+\frac{av}{(s+a+b)(s+a)}\biggr ]>0, \end{aligned}$$

(40)

Thus $h(s)$ is a continuous, differentiable and one-to-one map with respect to the variable $s>0$ such that the inverse function of $h(s)$ exists and is globally unique. Moreover, we can verify that $h(0)=0$ and $\lim \limits _{s\rightarrow \infty }h(s)=1$.

In the following, we show how we use $h(s)$ and $e^{-k_{el}\tau }$ to ensure the existence and uniqueness of $C^*$. Here for each dosing interval $\tau$ we have $e^{-k_{el}\tau }\in (0,1)$ such that there exists a unique $C^*$ satisfying Eq. 29. Moreover, $C^*$ is a monotonically decreasing function with respect to dosing interval $\tau$. In other words, the longer is the dosing interval, the smaller is the value of $e^{-k_{el}\tau }$ and then the smaller is the solution $C^*$ to be obtained (Fig. 9). However, if the dosing interval $\tau$ is fixed, $C^*$ would be monotonically increasing with the dose $D$ (Fig. 9).

Fig. 9

Unique existence of the solution $C^*$ of Eq. 29: $C^*$ is an increasing function with respect to dose $D$, here we take $CL_l= 0.4$ ml/h, $K_m = 1$ $\upmu$g/ml, $V_{max} = 0.4$ $\upmu$g/h, $V_d = 1\,\,ml$; $\tau = 1$ h; $D_{small} = 1$ $\upmu$g and $D_{large}=3\,\,ug$

Appendix B

In the following, we show that the periodic solution given by Eqs. 31 is locally asymptotically stable.

Theorem 1

The periodic solution given by Eqs. 31 is locally stable.

Proof

The model solutions described by Eqs. 20–21 will asymptotically approach the periodic solution given by Eqs. 31, for any given initial dose.

In terms of Eq. 25, we define a stroboscopic map ${\mathcal {M}}: C((n-1)\tau ^+)\in (0,\infty )\longmapsto C(n\tau ^+)\in (0,\infty )$ in the sense that

$$\begin{aligned} C(n\tau ^+)&= \beta \cdot X(g(C((n-1)\tau ^+),n\tau ),p_1,p_2)+D/V_d\nonumber \\&\mathop {=}\limits ^{def}{\mathcal {M}}(C((n-1)\tau ^+)). \end{aligned}$$

(41)

We have shown that the fixed point of the map ${\mathcal {M}}(C((n-1)\tau ^+))$, denoted $C^{**}=C^*+D/V_d$ and $C^*$ expressed by Eq. 30, uniquely exists. Then solution $C^{**}$ at equilibrium is locally stable provided that the following condition

$$\begin{aligned} \frac{\partial {\mathcal {M}}(C((n-1)\tau ^+))}{\partial C((n-1)\tau ^+)}\Bigl |_{C((n-1)\tau ^+)=C^{**}}< 1. \end{aligned}$$

(42)

is satisfied.

To show this, let $\displaystyle z=g(C((n-1)\tau ^+),n\tau )$, and according to the chain rule, we have

$$\begin{aligned}&\frac{\partial {\mathcal {M}}(C((n-1)\tau ^+))}{\partial C((n-1)\tau ^+)}\Bigl |_{C((n-1)\tau ^+)=C^{**}}\nonumber \\&= \beta \cdot X_z'(z,p_1,p_2)\Bigl |_{C((n-1)\tau ^+)=C^{**}}\cdot \frac{\partial z}{\partial C((n-1)\tau ^+)}\Bigl |_{C((n-1)\tau ^+)=C^{**}}. \end{aligned}$$

(43)

On the one hand, replacing $t$ by $n\tau$ in the definition of $g$ function, we obtain

$$\begin{aligned}&\frac{\partial z}{\partial C((n-1)\tau )}\Bigl |_{C((n-1)\tau ^+)=C^{**}}\nonumber \\&= e^{-\tau }\left( \frac{C^*+C_0}{\beta }\right) ^{p_1}\left( \frac{C^*+C_0}{\beta }+1\right) ^{p_2} \left[ \frac{p_1}{C^*+C_0}+\frac{p_2}{C^*+\beta +C_0}\right] . \end{aligned}$$

(44)

On the other hand, it follows from Eq. 25 that we have

$$\begin{aligned} X(z,p_1,p_2)\Bigl |_{C((n-1)\tau ^+)=C^{**}}=\dfrac{C^*}{\beta }. \end{aligned}$$

(45)

Moreover, the definition of $X$ function yields

$$\begin{aligned}&z\Bigl |_{C((n-1)\tau ^+)=C^{**}}\nonumber \\&= \left( \frac{C^*+C_0}{\beta }\right) ^{p_1}\left( \frac{C^*+C_0}{\beta }+1\right) ^{p_2}\cdot e^{-\tau }. \end{aligned}$$

(46)

Substituting Eqs. 45 and 46 into Eq. 11 yields

$$\begin{aligned}&X'_z(z,p_1,p_2)\Bigl |_{C((n-1)\tau ^+)=C^{**}}\nonumber \\&= \frac{1}{z\left[ \frac{p_1}{X(z,p_1,p_2)}+\frac{p_2}{1+X(z,p_1,p_2)}\right] }\Bigl |_{C((n-1)\tau ^+)=C^{**}}\nonumber \\&= \frac{e^{\tau }}{\left( \frac{C^*+C_0}{\beta }\right) ^{p_1}\left( \frac{C^*+C_0}{\beta }+1\right) ^{p_2}\left[ \frac{\beta p_1}{C^*}+\frac{\beta p_2}{C^*+\beta }\right] }. \end{aligned}$$

(47)

Substituting Eqs. 44, 47 into Eq. 43, we have

$$\begin{aligned} \frac{\partial {\mathcal {M}}(C((n-1)\tau ^+))}{\partial C((n-1)\tau ^+)}\Bigl |_{C((n-1)\tau ^+)=C^{**}} =\frac{\frac{p_1}{C^*+C_0}+\frac{p_2}{C^*+\beta +C_0}}{\frac{p_1}{C^*}+\frac{p_2}{C^*+\beta }}<1, \end{aligned}$$

(48)

which implies the local stability of the steady-state $C^{**}$. $\square$