Skip to main content
SpringerLink
Log in

Two-oscillator Kantowski–Sachs model of the Schwarzschild black hole interior

  • Research Article
  • Published:
General Relativity and Gravitation Aims and scope Submit manuscript

Abstract

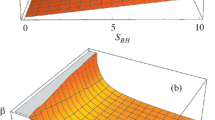
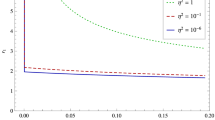
In this paper the interior of the Schwarzschild black hole, which is presented as a vacuum, homogeneous and anisotropic Kantowski–Sachs minisuperspace cosmological model, is considered. Lagrangian of the model is reduced by a suitable coordinate transformation to Lagrangian of two decoupled oscillators with the same frequencies and with zero energy in total (an oscillator-ghost-oscillator system). The model is presented in a classical, a p-adic and a noncommutative case. Then, within the standard quantum approach Wheeler–DeWitt equation and its general solutions, i.e. a wave function of the model is written, and then an adelic wave function is constructed. Finally, thermodynamics of the model is studied by using the Feynman–Hibbs procedure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abbott, B.P., et al.: (LIGO Scientific Collaboration and Virgo Collaboration): Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016). doi:10.1103/PhysRevLett.116.061102

    Article  ADS  Google Scholar 

  2. DeWitt, B.S.: Quantum theory of gravity. I. The canonical theory. Phys. Rev. 160, 1113–1148 (1967)

    Article  ADS  MATH  Google Scholar 

  3. Hartle, J.B., Hawking, S.W.: Wave function of the universe. Phys. Rev. D 28, 2960–2975 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  4. Vilenkin, A.: Creation of universes from nothing. Phys. Lett. B 117, 25–28 (1982)

    Article  ADS  MathSciNet  Google Scholar 

  5. Vladimirov, V.S., Volovich, I.V., Zelenov, E.I.: \(p\)-Adic Analysis and Mathematical Physics. World Scientific, Singapore (1994)

    Book  MATH  Google Scholar 

  6. Djordjevic, G.S., Dragovich, B., Nesic, Lj, Volovich, I.V.: \(p\)-Adic and adelic minisuperspace quantum cosmology. Int. J. Mod. Phys. A 17, 1413–1433 (2002)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. Wigner, E.: On the quantum correction for thermodynamic equilibrium. Phys. Rev. 40, 749–759 (1932)

    Article  ADS  MATH  Google Scholar 

  8. Snyder, H.S.: Quantized space-time. Phys. Rev. 71, 38–41 (1947)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  9. Connes, A.: Noncommutative differential geometry. Inst. Hautes Etudes Sci. Publ. Math. 62, 257–360 (1985)

    Article  MathSciNet  Google Scholar 

  10. Woronowicz, S.L.: Twisted SU(2) group: an example of a noncommutative differential calculus. Publ. Res. Inst. Math. Sci. 23, 117–181 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  11. Wess, J., Zumino, B.: Covariant differential calculus on the quantum hyperplane. Nucl. Phys. B Proc. Suppl. 18, 302–312 (1990)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  12. Várilly, J.C.: The Interface of noncommutative geometry and physics. In: Clifford Algebras. Progress in Mathematical Physics, vol. 34, pp. 227–242. Birkhäuser, Boston (2004)

  13. Maceda, M., Madore, J., Manousselis, P., Zoupanos, G.: Can noncommutativity resolve the big-bang singularity? Eur. Phys. J. C 36, 529–534 (2004)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Jalalzadeh, S., Vakili, B.: Quantization of the interior Schwarzschild black hole. Int. J. Theor. Phys. 51, 263–275 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Brehme, R.W.: Inside the black hole. Am. J. Phys. 45, 423–428 (1977)

    Article  ADS  Google Scholar 

  16. Djordjevic, G.S., Dragovich, B., Nesic, Lj: Adelic path integrals for quadratic actions. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 6, 179–195 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  17. Djordjevic, G.S., Nesic, L.J., Radovancevic, D.: Signature change in \(p\)-adic and noncommutative FRW cosmology. Int. J. Mod. Phys. A (2014). doi:10.1142/S0217751X14501553

    MathSciNet  MATH  Google Scholar 

  18. Dragovich, B., Rakic, Z.: Path integrals in noncommutative quantum mechanics. Theor. Math. Phys. 140, 1299–1308 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  19. Sepangi, H.R., Shakerin, B., Vakili, B.: Deformed phase space in a two-dimensional minisuperspace model. Class. Quantum Gravity (2009). doi:10.1088/0264-9381/26/6/065003

    MathSciNet  MATH  Google Scholar 

  20. Lopez-Dominguez, J.C., Obregon, O., Ramirez, C., Sabido, M.: Towards noncommutative quantum black holes. Phys. Rev. D (2006). doi:10.1103/PhysRevD.74.084024

    MathSciNet  Google Scholar 

  21. Bastos, C., Bertolami, O., Dias, N.C., Prata, J.N.: Black holes and phase-space noncommutativity. Phys. Rev. D (2009). doi:10.1103/PhysRevD.80.124038

    MathSciNet  MATH  Google Scholar 

  22. Bastos, C., Bertolami, O., Dias, N.C., Prata, J.N.: Noncanonical phase-space noncommutativity and the Kantowski-Sachs singularity for black holes. Phys. Rev. D (2011). doi:10.1103/PhysRevD.84.024005

    MATH  Google Scholar 

  23. Conradi, H.D.: Quantum cosmology of Kantowski–Sachs like models. Class. Quantum Gravity 12, 2423–2440 (1995)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Kiefer, C.: Wave packets in quantum cosmology and the cosmological constant. Nucl. Phys. B 341, 273–293 (1990)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  25. Dragovich, B.: Adelic harmonic oscillator. Int. J. Mod. Phys. A 10, 2349–2365 (1995)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. Feynman, R.P., Hibbs, A.R.: Quantum Mechanics and Path Integrals. McGraw-Hill, New York (1965)

    MATH  Google Scholar 

  27. Ashtekar, A., Baez, J., Corichi, A., Krasnov, K.: Quantum geometry and black hole entropy. Phys. Rev. Lett. 80, 904–907 (1998)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  28. Vaz, C.: Canonical quantization and the statistical entropy of the Schwarzschild black hole. Phys. Rev. D (2000). doi:10.1103/PhysRevD.61.064017

    MathSciNet  Google Scholar 

  29. Gour, G.: Schwarzschild black hole as a grand canonical ensemble. Phys. Rev. D (2000). doi:10.1103/PhysRevD.61.021501

    MathSciNet  Google Scholar 

  30. Mukherji, S., Pal, S.S.: Logarithmic corrections to black hole entropy and AdS/CFT correspondence. J. High Energy Phys. (2002). doi:10.1088/1126-6708/2002/05/026

    MathSciNet  Google Scholar 

  31. Meissner, K.A.: Black hole entropy in loop quantum gravity. Class. Quantum Gravity 21, 5245–5252 (2004)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. Corichi, A., Diaz-Polo, J., Fernandez-Borja, E.: Quantum geometry and microscopic black hole entropy. Class. Quantum Gravity 24, 243–251 (2007)

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The work of G. Djordjevic and Lj. Nesic is partially supported by Ministry of Education, Science and Technological Development of the Republic of Serbia under Grant Nos. 174020 and 176021, and ICTP-SEENET-MTP Project PRJ09 Cosmology and Strings in the frame of the Southeastern European Network in Theoretical and Mathematical Physics, the work of D. Radovancevic is partially supported within this frame, as well. G. Djordjevic is thankful to the CERN-TH group for financial support and hospitality during his stay, where a part of this paper was finalized.

Author information

Authors and Affiliations

  1. Faculty of Science and Mathematics, University of Nis, P.O. Box 224, Nis, 18000, Serbia

    Goran S. Djordjevic, Ljubisa Nesic & Darko Radovancevic

Authors
  1. Goran S. Djordjevic
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ljubisa Nesic
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Darko Radovancevic
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Darko Radovancevic.

Appendix: Coefficients \(\alpha _{ij}\) and \(K_i^\pm \)

Appendix: Coefficients \(\alpha _{ij}\) and \(K_i^\pm \)

If \(A=\frac{2\theta \omega ^2{\varOmega }_1}{\omega _\theta ^2-{\varOmega }_1^2}\), \(B=\frac{2\theta \omega ^2{\varOmega }_2}{\omega _\theta ^2-{\varOmega }_2^2}\) and

\({\varDelta }=-2AB[1-\cos ({\varOmega }_1T)\cos ({\varOmega }_2T)]+(A^2+B^2)\sin ({\varOmega }_1T)\sin ({\varOmega }_2T)\not =0\), then:

$$\begin{aligned} \alpha _{11}= & {} \frac{1}{{\varDelta }}\left[ -AB+B^2\sin \left( {\varOmega }_1T\right) \sin \left( {\varOmega }_2T\right) +AB\cos \left( {\varOmega }_1T\right) \cos \left( {\varOmega }_2T\right) \right] , \nonumber \\ \alpha _{12}= & {} \frac{1}{{\varDelta }}\left[ AB\left( \cos \left( {\varOmega }_2T\right) -\cos \left( {\varOmega }_1T\right) \right) \right] , \nonumber \\ \alpha _{13}= & {} \frac{1}{{\varDelta }}\left[ B\sin \left( {\varOmega }_1T\right) \cos \left( {\varOmega }_2T\right) -A\sin \left( {\varOmega }_2T\right) \cos \left( {\varOmega }_1T\right) \right] , \nonumber \\ \alpha _{14}= & {} \frac{1}{{\varDelta }}\left[ A\sin \left( {\varOmega }_2T\right) -B\sin \left( {\varOmega }_1T\right) \right] , \nonumber \\ \alpha _{21}= & {} \frac{1}{{\varDelta }}\left[ AB\sin \left( {\varOmega }_1T\right) \cos \left( {\varOmega }_2T\right) -B^2\cos \left( {\varOmega }_1T\right) \sin \left( {\varOmega }_2T\right) \right] , \nonumber \\ \alpha _{22}= & {} \left. \frac{1}{{\varDelta }}\left[ B^2\sin \left( {\varOmega }_2T\right) -AB\sin \left( {\varOmega }_1T\right) \right) \right] , \nonumber \\ \alpha _{23}= & {} \frac{1}{{\varDelta }}\left[ B-B\cos \left( {\varOmega }_1T\right) \cos \left( {\varOmega }_2T\right) -A\sin \left( {\varOmega }_1T\right) \sin \left( {\varOmega }_2T\right) \right] , \nonumber \\ \alpha _{24}= & {} \frac{1}{{\varDelta }}\left[ B\left( \cos \left( {\varOmega }_1T\right) -\cos \left( {\varOmega }_2T\right) \right) \right] , \nonumber \\ \alpha _{31}= & {} \frac{1}{{\varDelta }}\left[ -AB+AB\cos \left( {\varOmega }_1T\right) \cos \left( {\varOmega }_2T\right) +A^2\sin \left( {\varOmega }_1T\right) \sin \left( {\varOmega }_2T\right) \right] , \nonumber \\ \alpha _{32}= & {} \frac{1}{{\varDelta }}\left[ AB\left( \cos \left( {\varOmega }_1T\right) -\cos \left( {\varOmega }_2T\right) \right) \right] , \nonumber \\ \alpha _{33}= & {} \frac{1}{{\varDelta }}\left[ A\sin \left( {\varOmega }_2T\right) \cos \left( {\varOmega }_1T\right) -B\sin \left( {\varOmega }_1T\right) \cos \left( {\varOmega }_2T\right) \right] , \nonumber \\ \alpha _{34}= & {} \frac{1}{{\varDelta }}\left[ A\sin \left( {\varOmega }_2T\right) -B\sin \left( {\varOmega }_1T\right) \right] , \nonumber \\ \alpha _{41}= & {} \frac{1}{{\varDelta }}\left[ AB\cos \left( {\varOmega }_1T\right) \sin \left( {\varOmega }_2T\right) -A^2\sin \left( {\varOmega }_1T\right) \cos \left( {\varOmega }_2T\right) \right] , \nonumber \\ \alpha _{42}= & {} \frac{1}{{\varDelta }}\left[ A^2\sin \left( {\varOmega }_1T\right) -AB\sin \left( {\varOmega }_2T\right) \right] , \nonumber \\ \alpha _{43}= & {} \frac{1}{{\varDelta }}\left[ A-B\sin \left( {\varOmega }_1T\right) \sin \left( {\varOmega }_2T\right) -A\cos \left( {\varOmega }_1T\right) \cos \left( {\varOmega }_2T\right) \right] , \nonumber \\ \alpha _{44}= & {} \frac{1}{{\varDelta }}\left[ A\left( \cos \left( {\varOmega }_2T\right) -\cos \left( {\varOmega }_1T\right) \right) \right] . \end{aligned}$$
(75)
$$\begin{aligned} K_1^{\pm }= & {} K_1^{\pm }\left( {\varOmega }_1\right) =\left( 1{\mp }A^2\right) \left[ \left( 1+\theta ^2\omega ^2\right) {\varOmega }_1^2{\mp }\omega ^2\right] -2\theta {\varOmega }_1A\left( \omega ^2\pm \omega ^2\right) , \nonumber \\ K_2^{\pm }= & {} K_2^{\pm }\left( {\varOmega }_2\right) =\left( 1{\mp }B^2\right) \left[ \left( 1+\theta ^2\omega ^2\right) {\varOmega }_2^2{\mp }\omega ^2\right] -2\theta {\varOmega }_2B\left( \omega ^2\pm \omega ^2\right) , \nonumber \\ K_3^{\pm }= & {} K_3^{\pm }\left( {\varOmega }_1,{\varOmega }_2\right) =\left[ \left( 1+\theta ^2\omega ^2\right) {\varOmega }_1{\varOmega }_2{\mp }\omega ^2\right] \left( 1{\mp }AB\right) {\mp }\left( A{\pm }B\right) \theta \omega ^2\left( {\varOmega }_1{\pm }{\varOmega }_2\right) .\nonumber \\ \end{aligned}$$
(76)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Djordjevic, G.S., Nesic, L. & Radovancevic, D. Two-oscillator Kantowski–Sachs model of the Schwarzschild black hole interior. Gen Relativ Gravit 48, 106 (2016). https://doi.org/10.1007/s10714-016-2102-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10714-016-2102-x

Keywords

Search

Navigation