Abstract
A marked lattice is a d-dimensional Euclidean lattice, where each lattice point is assigned a mark via a given random field on \({\mathbb {Z}}^d\). We prove that, if the field is strongly mixing with a faster-than-logarithmic rate, then for every given lattice and almost every marking, large spheres become equidistributed in the space of marked lattices. A key aspect of our study is that the space of marked lattices is not a homogeneous space, but rather a non-trivial fiber bundle over such a space. As an application, we prove that the free path length in a crystal with random defects has a limiting distribution in the Boltzmann-Grad limit.
Similar content being viewed by others
1 Introduction
Consider a Lie group G, a non-compact one-parameter subgroup \(\Phi ^{\mathbb {R}}\) and a compact subgroup K. Let \(\lambda \) be a probability measure on K that is absolutely continuous with respect to Haar measure on K. Given a measure-preserving action \(G\times X\rightarrow X\), \((g,x)\mapsto xg\) on a probability space \((X,{\mathscr {A}},\mu )\), it is natural to ask under which conditions the “spherical” average \(P_t\) defined by \(P_t f:=\int _K f(x_0 k \Phi ^t) d\lambda (k)\) converges weakly to \(\mu \), or any other probability measure. In general the best one can hope for is convergence for \(\mu \)-almost all \(x_0\). Proofs typically require an additional average over \(\Phi ^t\), and may be viewed as generalizations of the classic Wiener ergodic theorem; see Nevo’s survey [21] and references therein. If the space X is homogeneous, then the weak convergence of the spherical average \(P_t\) can be proved for all \(x_0\), with a complete classification of all limit measures, by means of measure rigidity techniques that are based on Ratner’s measure classification theorem for subgroups generated by unipotent elements [22]. There is now a large body of literature on this topic, see for instance [7, 8, 16, 17, 19, 24]. In some settings, spherical equidistribution may also be deduced directly from the mixing property of \(\Phi ^{\mathbb {R}}\) [7]. The first example of spherical equidistribution in the non-homogeneous setting for all (and not just almost all) \(x_0\) is given in [10], where the analogue of Ratner’s theorem is proved for the moduli space of branched covers of Veech surfaces, which is a fiber bundle over a homogeneous space. A major advance in this direction is the recent work by Eskin and Mirzakhani [11] and Eskin, Mirzakhani and Mohammadi [12], who prove a Ratner-like classification of measures in the moduli space of flat surfaces that are invariant under the upper triangular subgroup of \({\text {SL}}(2,\mathbb {R})\). This is used to prove convergence of spherical averages in that moduli space, with an additional t average as above, which yields an averaged counting asymptotics for periodic trajectories in general rational billiards.
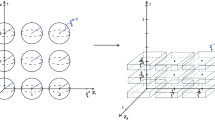
The goal of the present study is to construct a natural example of a non-homogeneous space (the space of marked Euclidean lattices), which is a fiber bundle over a homogeneous space (the space of Euclidean lattices), and to prove spherical equidistribution for every point in the base and almost every point in the fiber. Our findings complement a theorem of Brettschneider [3, Theorem 4.7], who proves uniform convergence of Birkhoff averages for fiber bundles with uniquely ergodic base under technical assumptions on the test function and fiber transformation.
This paper is organized as follows. We introduce the space of lattices in Sect. 2, then the space of marked lattices in Sect. 3, where the marking is produced by a random field on \({\mathbb {Z}}^d\). The main results of this study, limit theorems for spherical averages in the space of marked lattices, are stated and proved in Sects. 4 and 5. The former deals with convergence on average over the field, the latter with a fixed realization of the random field. Section 6 applies these results to the setting of defect lattices, where lattice points are either randomly removed, or shifted from their equilibrium position. Section 7 explains how these findings can be used to calculate the limit distribution for the free paths lengths in the Boltzmann–Grad limit of a Lorentz gas for such scatterer configurations.
2 Spherical averages in the space of lattices
Let \(G_0={\text {SL}}(d,\mathbb {R})\) and let \(\Gamma _0={\text {SL}}(d,\mathbb {Z})\). We represent elements in \(\mathbb {R}^d\) as row vectors, and define a natural action of \(G_0\) on \(\mathbb {R}^d\) by right matrix multiplication. The map
gives a one-to-one correspondence between the homogeneous space \(\Gamma _0\backslash G_0\) and the space of Euclidean lattices in \(\mathbb {R}^d\) of covolume one. The Haar measure \(\mu _0\) on \(G_0\) is normalized, so that it projects to a probability measure on \(\Gamma _0\backslash G_0\) which will also be denoted by \(\mu _0\).
Let \(G= G_0\ltimes \mathbb {R}^d\) be the semidirect product with multiplication law
where \({\varvec{\xi }},{\varvec{\xi }}'\) are viewed as row vectors. The group \(G\) is a bundle over \(G_0\) with fiber \(\mathbb {R}^d\). The subgroup \(\Gamma = \Gamma _0\ltimes \mathbb {Z}^d\) is a lattice in G. The Haar measure on G is \(\mu =\mu _0\times {{\mathrm{Leb}}}_{{\mathbb {R}}^d}\). It induces a probability measure on \(\Gamma \backslash G\) which will also be denoted by \(\mu \). The groups \(G_0\) and \(G\) act on \(\mathbb {R}^d\) by linear and affine transformations, respectively, which are given by
and
where concatenation denotes matrix multiplication. We embed \(G_0\hookrightarrow G\) by \(M\mapsto (M,{\varvec{0}})\), and identify \(G_0\) with its image under this embedding.
As in the linear case, the map
gives a one-to-one correspondence between the homogeneous space \(\Gamma \backslash G\) and the space of affine Euclidean lattices in \(\mathbb {R}^d\) of covolume one.
We will need other subgroups of \(G\) in addition to \(G_0\). For \({\varvec{\xi }}\in \mathbb {R}^d\), put
The subgroup \(\Gamma _{\varvec{\xi }}= \Gamma \cap G_{\varvec{\xi }}\) is a lattice in \(G_{\varvec{\xi }}\). We denote by \(\mu _{{\varvec{\xi }}}\) be the Haar measure on \(G_{\varvec{\xi }}\), normalized so that a fundamental domain of the \(\Gamma _{\varvec{\xi }}\)-action in \(G_{\varvec{\xi }}\) has measure 1. We denote the induced probability measure on \(\Gamma _{\varvec{\xi }}\backslash G_{\varvec{\xi }}\) also by \(\mu _{{\varvec{\xi }}}\). When \({\varvec{\xi }}\notin \mathbb {Q}^d\), we put \(\Gamma _{\varvec{\xi }}= \Gamma \) and \(\mu _{{\varvec{\xi }}} = \mu \). Thus, when \({\varvec{\xi }}\in \mathbb {Q}^d\), \(\mu _{{\varvec{\xi }}}\) can be identified with a singular measure on \(\Gamma \backslash G\) supported on the closed subspace \(\Gamma \backslash \Gamma G_{\varvec{\xi }}\simeq \Gamma _{\varvec{\xi }}\backslash G_{\varvec{\xi }}\) of X. Define the translate
again a closed subspace of X, which we equip with the subspace topology. Note that \(X_{\varvec{\xi }}=\overline{\Gamma \backslash \Gamma (\mathbbm {1},{\varvec{\xi }}) G_0}\). The measure \({\widetilde{\mu }}_{\varvec{\xi }}\) on \(X_{\varvec{\xi }}\) defined as the translate of \(\mu _{{\varvec{\xi }}}\),
for any Borel set \(A\subset X_{\varvec{\xi }}\). For \(t\in \mathbb {R}\) and \({\varvec{u}}\in U\subset \mathbb {R}^{d-1}\), with U open and bounded, define the matrices
The map \(U\rightarrow {\text {S}}_1^{d-1}\), \({\varvec{u}}\mapsto {\varvec{e}}_1 R({\varvec{u}})^{-1}\), where \({\varvec{e}}_1\) is the first standard basis vector, is a diffeomorphism onto its image if U is sufficiently small; cf. Remark 5.5 in [17]. More generally, we can take any smooth map \(E:U\rightarrow {\text {SO}}(d)\) such that
is invertible and the inverse is uniformly Lipschitz. We will furthermore assume in the following that the closure of \(\widetilde{E}(U)\) is contained in the hemisphere \(\{ {\varvec{v}}\in {\text {S}}_1^{d-1} : {\varvec{e}}_1\cdot {\varvec{v}}>0\}\), and that \({{\mathrm{Leb}}}(\partial U) = 0\).
For a given absolutely continuous probability measure \(\lambda \) on U, \(t\geqslant 0\) and \({\varvec{\xi }}\in \mathbb {R}^d\), \(M \in G_0\), let \(P_t=P_t^{(\lambda ,M,{\varvec{\xi }})}\) be the Borel probability measure on \(X_{\varvec{\xi }}\) defined by
for any bounded continuous \(f:X_{\varvec{\xi }}\rightarrow \mathbb {R}\). Note that the restriction to maps \(E:U\rightarrow {\text {SO}}(d)\) is purely for technical convenience. There is no loss of generality, since M is arbitrary and the maps \(U\mapsto {\text {S}}_1^{d-1}\), \({\varvec{u}}\mapsto {\varvec{e}}_1 E({\varvec{u}})^{-1} M^{-1}\) cover the sphere for finitely many choices of \(M\in {\text {SO}}(d)\); cf. [17].
Theorem 2.1
([17, Sec. 5]) For \(t\rightarrow \infty \),
Recall the above weak convergence means that for every bounded continuous \(f:X_{\varvec{\xi }}\rightarrow \mathbb {R}\), \(\lim _{t\rightarrow \infty } P_t f = {\widetilde{\mu }}_{\varvec{\xi }}f\).
We will now show how the space of lattices can be viewed as a subspace of the space of point processes in \({\mathbb {R}}^d\). The extension of this to marked point processes will be a key element in this paper.
Let \({\mathcal {M}}({\mathbb {R}}^d)\) be the space of locally finite Borel measures on \({\mathbb {R}}^n\), equipped with the vague topology. The vague topology is the smallest topology such that the function
is continuous for every \(f\in C_c({\mathbb {R}}^d)\) (the space of continuous functions \({\mathbb {R}}^d\rightarrow {\mathbb {R}}\) with compact support). The space \({\mathcal {M}}({\mathbb {R}}^d)\) is Polish in this topology [13, Theorem A 2.3]. We embed the space of affine lattices in \({\mathcal {M}}({\mathbb {R}}^d)\) by the map
For technical reasons (which will become clear in Corollary 2.4) we will need to treat the space of lattices \(X_0\) slightly differently; define
Proposition 2.2
The maps \(\iota \) and \(\iota _0\) are topological embeddings.
Proof
To establish the continuity of \(\iota \), we need to show that, for every \(f\in C_c({\mathbb {R}}^d)\), \(x_j\rightarrow x\) in X implies \(\iota (x_j)f \rightarrow \iota (x) f\). By the \(\Gamma \)-equivariance of \(\iota \), it is sufficient to show that \(g_j\rightarrow g\) in G implies
Let A be the compact support of f. Since \(g_j\rightarrow g\), the closure of \(A'=\cup _j (Ag_j^{-1})\) is compact. Hence \({\mathbb {Z}}^d\cap A'\) is finite. For \({\varvec{a}}\in {\mathbb {Z}}^d\setminus A'\) we have \(f({\varvec{a}}g_j)=f({\varvec{a}}g)=0\), and for the finitely many \({\varvec{a}}\in {\mathbb {Z}}^d\cap A'\) we have \(f({\varvec{a}}g_j)\rightarrow f({\varvec{a}}g)\).
The map \(\iota \) is injective, since the lattice \({\mathbb {Z}}^d x\) uniquely determines \(x\in \Gamma \backslash G\). Let \(\tilde{\iota }:X \rightarrow \iota (X)\), \(x\mapsto \iota (x)\). To establish the continuity of \(\tilde{\iota }^{-1}\), we need to show that \(\iota (x_j)f \rightarrow \iota (x) f\) for every \(f\in C_c({\mathbb {R}}^d)\) implies \(x_j\rightarrow x\) in X. Fix \(g=(M,{\varvec{\xi }})\in \Gamma x\). Then \({\varvec{e}}_1 M,\ldots ,{\varvec{e}}_n M\) forms a basis of \({\mathbb {Z}}^d M\), where \({\varvec{e}}_k\) are the standards basis vectors of \({\mathbb {Z}}^d\). Set \({\varvec{e}}_0={\varvec{0}}\) and define for \(k=0,1,\ldots ,n\),
Note that \(f_{k,\delta } \in C_c({\mathbb {R}}^d)\). By the discreteness of \({\mathbb {Z}}^d g\), there is \(\delta _0>0\) such that for all \(\delta \in (0,\delta _0]\), all \(k=0,1,\ldots ,n\),
Since by assumption \(\iota (x_j)f_{k,\delta } \rightarrow \iota (x) f_{k,\delta }=1\), given \(\delta >0\), there is \(j_0\in {\mathbb {N}}\) such that for every \(j\geqslant j_0\) and for every k, there is at least one element in \({\mathbb {Z}}^d x_j\) within distance \(\delta \) to \({\varvec{e}}_k g\). Call this element \({\varvec{y}}_k^{(j)}\). Then
and therefore
Because of this and the fact that the lattices \({\mathbb {Z}}^d x_j-{\varvec{y}}_0^{(j)}\) and \({\mathbb {Z}}^d x-{\varvec{\xi }}\) both have covolume one, the vectors \({\varvec{y}}_1^{(j)}-{\varvec{y}}_0^{(j)},\ldots ,{\varvec{y}}_n^{(j)}-{\varvec{y}}_0^{(j)}\) form a basis of \({\mathbb {Z}}^d x_j-{\varvec{y}}_0^{(j)}\) (for all sufficiently large j). Then
Now (2.21) implies \(g_j=(M_j,{\varvec{\xi }}_j)\rightarrow g=(M,{\varvec{\xi }})\) and thus \(x_j\rightarrow x\).
The proof for \(\iota _0\) is almost identical. \(\square \)
Every random element \(\zeta \) in X defines a point process \(\Theta =\iota (\zeta )\) in \({\mathcal {M}}({\mathbb {R}}^d)\). Let \(\zeta _t\) be the random element distributed according to \(P_t\), and \(\zeta \) according to \({\widetilde{\mu }}_{\varvec{\xi }}\), with \({\varvec{\xi }}\notin {\mathbb {Z}}^d\). Theorem 2.1 can then be rephrased as \(\zeta _t \,\,\buildrel \mathrm{d}\over \longrightarrow \,\,\zeta \). In view of Proposition 2.2 and the continuous mapping theorem [13, Theorem 4.27], this is equivalent to the following convergence in distribution for the point processes \(\Theta _t=\iota (\zeta _t)\) and \(\Theta =\iota (\zeta )\) in the case \({\varvec{\xi }}\notin {\mathbb {Z}}^d\), \(\Theta _{0,t}=\iota _0(\zeta _t)\) and \(\Theta _0=\iota _0(\zeta )\) for \({\varvec{\xi }}\in {\mathbb {Z}}^d\). To simplify notation we suppress the dependence on \({\varvec{\xi }}\); \(\Theta \) depends on the choice of \({\varvec{\xi }}\in {\mathbb {R}}^d\setminus {\mathbb {Z}}^d\).
Theorem 2.3
For \(t\rightarrow \infty \),
We now turn to the finite-dimensional distribution of the above point processes, cf. [17, Sec. 5].
Corollary 2.4
Let \(n\in {\mathbb {N}}\) and \(A_1,\ldots ,A_n\subset {\mathbb {R}}^d\) bounded Borel sets with \({{\mathrm{Leb}}}(\partial A_i) = 0\) for all i. Then, for \(t\rightarrow \infty \),
In view of [13, Theorem 16.16], the main ingredient in the derivation of Corollary 2.4 from Theorem 2.3 is to show that \({{\mathrm{Leb}}}(\partial A_i) = 0\) implies that \(\Theta \partial A_i=0\) almost surely, and \(\Theta _0 \partial A_i=0\) almost surely. This follows from Siegel’s integral formula [25, 26], which says that \({{\mathrm{\mathbb {E}}}}\Theta _0 B={{\mathrm{Leb}}}(B)\), \({{\mathrm{\mathbb {E}}}}\Theta B={{\mathrm{Leb}}}(B)\) for every \(B\in {\mathscr {B}}({\mathbb {R}}^d)\) (note that this identity is straightforward for \({\varvec{\xi }}\notin {\mathbb {Q}}^d\), since it follows directly from the translation invariance of \(\Theta \)). Note that \(\Theta \partial A_i=0\) fails for \({\varvec{\xi }}\in {\mathbb {Z}}^d\) if \({\varvec{0}}\in \partial A_i\). This is the reason for removing \({\varvec{0}}\) in the definition (2.17) of \(\iota _0\). But Siegel’s formula implies \({{\mathrm{Leb}}}(\partial A_i) = 0\) if and only if \(\Theta _0 \partial A_i=0\) (resp. \(\Theta \partial A_i=0\)) almost surely. Therefore the statement of Corollary 2.4 is in fact equivalent to Theorem 2.3 via [13, Theorem 16.16]. We will exploit the analogue in the treatment of marked lattices.
The following lemmas will be useful below.
Lemma 2.5
For \(A\in {\mathscr {B}}({\mathbb {R}}^d)\),
Proof
This follows from Chebyshev’s inequality followed by Siegel’s formula. \(\square \)
Lemma 2.6
For \(A\in {\mathscr {B}}({\mathbb {R}}^d)\) and \(L \in \mathbb {Z}_{\geqslant 0}\),
and
Proof
See [15, Theorems 4.3, 4.5]. \(\square \)
3 Marked lattices and marked point processes
We will now extend the discussion in the previous section to the space of marked lattices, which is defined as a certain fiber bundle over the space of lattices. The key point is now to identify this space with a marked point process.
Each map \(\omega :{\mathbb {Z}}^d \rightarrow Y\), where Y is the set of marks, produces a marking of the affine lattice \({\mathbb {Z}}^d g\) with \(g\in G\): the point \({\varvec{y}}\in {\mathbb {Z}}^d g\) has mark \(\omega ({\varvec{y}}g^{-1})\). A Y-marked affine lattice is thus the point set
in \(\mathbb {R}^d\times Y\), and can be parametrized by the pair \((g,\omega )\in G \times \Omega \), where \(\Omega =\{ \omega : {\mathbb {Z}}^d \rightarrow Y\}\) is the set of all possible markings. Note that, for \(\gamma \in \Gamma \), the point \({\varvec{y}}={\varvec{m}}\gamma g\in {\mathbb {Z}}^d g\) has mark
where \(\omega _\gamma ({\varvec{m}}):=\omega ({\varvec{m}}\gamma )\). Hence \((g,\omega )\) and \((\gamma g,\omega _\gamma )\) yield the same marked affine lattice. This motivates the definition of the left action of \(\Gamma \) on \(G \times \Omega \) by \(\gamma (g,\omega ):=(\gamma g, \omega _\gamma )\). We define a right action of G on \(G \times \Omega \) by \((g,\omega ) g':=(g g', \omega )\). In analogy with the homogeneous space setting we define
and
For the case \({\varvec{\xi }}\in \mathbb {Z}^d\), we have
which in turn can be identified with the space \(\Gamma _0\backslash (G_0\times \Omega )\) via the map \(\Gamma ((M,{\varvec{0}}),\omega )\mapsto \Gamma _0(M,\omega )\). Note that the point \(\Gamma ((\mathbbm {1},{\varvec{\xi }}) M,\omega )=\Gamma (M, \omega _{(\mathbbm {1},-{\varvec{\xi }})})\) is mapped to \(\Gamma _0(M,\omega _{(\mathbbm {1},-{\varvec{\xi }})})\) under this identification.
Lemma 3.1
The map
yields a one-to-one correspondence between \({\mathcal {X}}\) and Y-marked affine lattices of covolume one.
Proof
For \((g,\omega )\) and \((g',\omega ')\) to yield the same marked lattice, it is necessary that \({\mathbb {Z}}^d g={\mathbb {Z}}^d g'\). Hence \(g'=\gamma g\) for some \(\gamma \in \Gamma \). But this implies \(\omega '=\omega _\gamma \) and hence \((g',\omega ')=\gamma (g,\omega )\). \(\square \)
We now extend the above correspondences to the topological setting. Let Y be a topological space, and endow the space of all markings \(\Omega =Y^{{\mathbb {Z}}^d}\) with the product topology. Define the topology of \(G\times \Omega \) by the product topology, and on \({\mathcal {X}}\), \({\mathcal {X}}_{\varvec{\xi }}\) by the quotient and subspace topology, respectively. If Y is locally compact second countable Hausdorff (lcscH), then \({\mathbb {R}}^d\times Y\) is lcscH. Consider the measurable space \((Y,{\mathscr {B}}(Y))\) with Borel \(\sigma \)-algebra \({\mathscr {B}}(Y)\), and define \({\mathcal {M}}({\mathbb {R}}^d\times Y)\) as the space of \(\sigma \)-finite Borel measures on \({\mathbb {R}}^d\times Y\) equipped with the vague topology. Under these assumptions, \({\mathcal {M}}({\mathbb {R}}^d\times Y)\) is Polish [13, Theorem A 2.3].
Set
and
These maps are well-defined and injective by Lemma 3.1. Note that \(\varkappa _0\) maps the point \(\Gamma ((\mathbbm {1},{\varvec{\xi }}) M,\omega )=\Gamma (M, \omega _{(\mathbbm {1},-{\varvec{\xi }})})\) with \({\varvec{\xi }}\in {\mathbb {Z}}^d\), \(M\in G_0\) to
Proposition 3.2
The maps \(\varkappa \) and \(\varkappa _0\) are topological embeddings.
Proof
To prove continuity of \(\varkappa \), we need to show that \((g_j,\omega _j)\rightarrow (g,\omega )\) in \(G\times \Omega \) implies
for every \(f\in C_c({\mathbb {R}}^d\times Y)\). As in the proof of Proposition 2.2, the compact support of f reduces the problem to showing that \(f({\varvec{a}}g_j,\omega _j({\varvec{a}}))\rightarrow f({\varvec{a}}g,\omega ({\varvec{a}}))\) for finitely many \({\varvec{a}}\in {\mathbb {Z}}^d\). The latter follows from the continuity of f.
Let \(\tilde{\varkappa }:{\mathcal {X}}\rightarrow \varkappa ({\mathcal {X}})\), \(x\mapsto \varkappa (x)\). To establish the continuity of \(\tilde{\varkappa }^{-1}\), we need to show that \(\varkappa (x_j)f \rightarrow \varkappa (x) f\) for every \(f\in C_c({\mathbb {R}}^d\times Y)\) implies \(x_j\rightarrow x\) in \({\mathcal {X}}\). We already know from Proposition 2.2 that \(g_j\rightarrow g\). Fix \({\varvec{m}}\in {\mathbb {Z}}^d\), and define for \(g\in G\), \(h\in C_c(Y)\),
Note that \(f_{h,\delta } \in C_c({\mathbb {R}}^d\times Y)\). By the discreteness of \({\mathbb {Z}}^d g\), there is \(\delta _0>0\) such that for all \(\delta \in (0,\delta _0]\),
Since \(g_j\rightarrow g\), for given \(\delta >0\), there is \(j_0\in {\mathbb {N}}\) such that for all \(j\geqslant j_0\),
Now \( \varkappa (x_j) f \rightarrow \varkappa (x) f\) for every \(f\in C_c({\mathbb {R}}^d\times Y)\) implies \(h(\omega _j({\varvec{m}}))\rightarrow h(\omega ({\varvec{m}}))\) for every fixed \(h\in C_c(Y)\) and \({\varvec{m}}\in {\mathbb {Z}}^d\). That is, \(\delta _{\omega _j({\varvec{m}})}\rightarrow \delta _{\omega ({\varvec{m}})}\) in \({\mathcal {M}}(Y)\). Any open set B containing \(\omega ({\varvec{m}})\) satisfies \(\delta _{\omega ({\varvec{m}})} B=1\) and \(\delta _{\omega ({\varvec{m}})}\partial B=0\). Thus \(\delta _{\omega _j({\varvec{m}})}B\rightarrow 1\) for any open set B containing \(\omega ({\varvec{m}})\) [13, Theorem A 2.3], and therefore \(\omega _j({\varvec{m}})\rightarrow \omega ({\varvec{m}})\). This implies \(\omega _j\rightarrow \omega \) in the product topology of \(\Omega \).
The proof for \(\varkappa _0\) is similar to the above, with the following modifications. Equation (3.10) is replaced by
for every \((f_1, f_2) \in C_c(Y)\times C_c(\mathbb {R}^d\times Y),\) which is seen to hold as in the argument for \(\varkappa \).
Let \({\tilde{\varkappa }}_0 :{\mathcal {X}}\rightarrow \varkappa _0({\mathcal {X}})\), \(x\mapsto \varkappa _0 (x)\). To establish continuity of \({\tilde{\varkappa }}_0^{-1}\), it is enough to show that
We know from Proposition 2.2 that \(g_j\rightarrow g\), and need to show that \(\omega _j\rightarrow \omega \). For any \({\varvec{m}}\in \mathbb {Z}^d\setminus \{{\varvec{0}}\}\), define \(f_{h_2,\delta }\) as in (3.11). It follows from discreteness of \(\mathbb {Z}^d g\) that there is \(\delta _0>0\) such that for all \(\delta \in (0,\delta _0]\),
Since \(g_j\rightarrow g\), we have
for all \(j\geqslant j_0\). Thus, we have
for all bounded continuous functions \(h_1\), \(h_2\) and \({\varvec{m}}\in \mathbb {Z}^d\setminus \{{\varvec{0}}\}\), inasmuch as \( (\delta _{\omega _j({\varvec{0}})}, \delta _{\omega _j({\varvec{m}})}) \rightarrow (\delta _{\omega ({\varvec{0}})}, \delta _{\omega ({\varvec{m}})}) \) in \({\mathcal {M}}(Y) \times {\mathcal {M}}(\mathbb {R}^d\times Y)\) for each \({\varvec{m}}\in \mathbb {Z}^d\setminus \{{\varvec{0}}\}\). This implies that \(\omega _j\rightarrow \omega \) in the product topology on \(\Omega \), as needed. \(\square \)
To define probability measures on the space \({\mathcal {X}}_{\varvec{\xi }}\) of affine marked lattices, let us fix a random field \(\eta :{\mathbb {Z}}^d\rightarrow Y\), \({\varvec{m}}\mapsto \eta ({\varvec{m}})\) defined by the probability measure \(\nu \) on the measurable space \((\Omega ,{\mathscr {B}})\) (where \({\mathscr {B}}={\mathscr {B}}(\Omega )\) is the Borel \(\sigma \)-algebra on \(\Omega =Y^{{\mathbb {Z}}^d}\) with respect to the product topology) via
for all \(A_1,\ldots ,A_k\in {\mathscr {B}}(Y)\). In other words, \(\eta \) is a random element in \(\Omega \) distributed according to \(\nu \).
We define the mixing coefficient of order k of the random field \(\eta \) by
where \(\Vert \cdot \Vert \) is the Euclidean norm, and
We say \(\eta \) is mixing of order k if
and mixing of all orders if it is mixing of order k for all \(k\in {\mathbb {N}}\). Note that mixing of order two need not imply mixing of order three; cf. Ledrappier’s “three dots” example [6, 14].
Given \({\varvec{\xi }}\in {\mathbb {R}}^d\) and a probability measure \(\rho \) on Y, we also define
If \(\lim _{s\rightarrow \infty }\beta _{{\varvec{0}}}(s)=0\), we say \(\eta \) has asymptotic distribution \(\rho \). The presence of \({\varvec{\xi }}\) in (3.25) is purely for notational convenience further on.
The above mixing conditions will be sufficient for the results in Sect. 4. We will need the following stronger variant for our main results in Sect. 5.
Given a non-empty subset \(J \subset {\mathbb {Z}}^d\) and a map \(a: J\rightarrow Y\), we define the cylinder set
The subalgebra generated by all cylinder sets \(\Omega _a\) for a given J is denoted by \({\mathscr {B}}_J\). The separation of two non-empty subsets \(J_1,J_2\subset {\mathbb {Z}}^d\) is defined as
We define the strong-mixing coefficient of the random field \(\eta \) by
where
We say \(\eta \) is strongly mixing if
Note that, in the case of singleton sets, we have
Thus strong mixing implies mixing of order two. In fact, strong mixing implies mixing of any order. This follows from the following observation. For \(k\geqslant 2\), put
where
Lemma 3.3
If \(\alpha (s)\rightarrow 0\) then \(\alpha _k(s)\rightarrow 0\) and \(\vartheta _k(s)\rightarrow 0\) for all \(k\geqslant 2\).
Proof
Note that \(\alpha _k(s)\rightarrow 0\) implies \(\vartheta _k(s)\rightarrow 0\), since
We will show that \(\alpha _k(s)\rightarrow 0\) implies \(\alpha _{k+1}(s)\rightarrow 0\). The claim then follows by induction on k. We have \({\mathscr {B}}_{J_i}\subset {\mathscr {B}}_J\) for \(J:=J_1\cup \cdots \cup J_k\) and therefore
This in turn implies
The first term equals \(\alpha (J,J_{k+1})\), and the second satisfies
because \(\nu (A_{k+1})\leqslant 1\). Therefore \(\alpha _{k+1}(s)\leqslant \alpha _k(s)+\alpha (s)\), which yields the desired conclusion. \(\square \)
An important example of a (strongly) mixing random field is the case when \(\eta \) is a field of i.i.d. random elements with law \(\rho \), and thus \(\alpha (s)=0\) for all s. In this case we write \(\nu =\nu _\rho \). Note that \(\nu _\rho \) is invariant under the \(\Gamma \)-action on \(\Omega \). Given such \(\nu _\rho \), consider the product measure \(\mu _{\varvec{\xi }}\times \nu _\rho \) on \(G_{\varvec{\xi }}\times \Omega \). We denote the push-forward of this measure (restricted to a fundamental domain for the \(\Gamma \)-action) under the projection map
by \({\widetilde{\mu }}_{{\varvec{\xi }},\rho }\). Recall \(\mu _{\varvec{\xi }}\) is normalized so that it projects to a probability measure on \(X_{\varvec{\xi }}\), which implies \({\widetilde{\mu }}_{{\varvec{\xi }},\rho }\) is a probability measure. Note that \({\widetilde{\mu }}_{{\varvec{\xi }},\rho }\) is well defined thanks to the \(\Gamma \)-invariance of \(\nu _\rho \).
A random element \(\zeta \) in \({\mathcal {X}}_{\varvec{\xi }}\) defines a point process \(\Xi =\varkappa (\zeta )\) in \({\mathcal {M}}({\mathbb {R}}^d\times Y)\). The Siegel formula for the space of lattices yields:
Lemma 3.4
Let \({\varvec{\xi }}\notin {\mathbb {Z}}^d\). For \(D\in {\mathscr {B}}({\mathbb {R}}^d\times Y)\),
Proof
It suffices to consider \(D=A\times B\) with \(A\in {\mathscr {B}}({\mathbb {R}}^d)\) and \(B\in {\mathscr {B}}(Y)\). Since the \(\eta ({\varvec{m}})\) are independent with law \(\rho \), we have \(\Xi D= \Theta (A) \rho (B)\). The expectation is \({{\mathrm{\mathbb {E}}}}\Xi D= {{\mathrm{\mathbb {E}}}}(\Theta A) \rho (B)={{\mathrm{Leb}}}(A)\rho (B)\) by Siegel’s formula. \(\square \)
A further special case is when \(\{\eta ({\varvec{m}}), {\varvec{m}}\in \mathbb {Z}^d\}\) is a collection of independent random variables with \(\eta ({\varvec{0}})\) distributed according to \(\rho _0\) and \(\eta ({\varvec{m}})\) distributed according to \(\rho \) when \({\varvec{m}}\ne {\varvec{0}}\). In this case we write \(\nu =\nu _{\rho _0,\rho }\). Note that \(\nu _{\rho _0,\rho }\) is now invariant under the \(\Gamma _0\)-action on \(\Omega \). Given such \(\nu _{\rho _0,\rho }\), consider the product measure \(\mu _0 \times \nu _{\rho _0,\rho }\) on \(G_0\times \Omega \). We denote the push-forward of this measure (restricted to a fundamental domain for the \(\Gamma _0\)-action) under the projection map
by \({\widetilde{\mu }}_{0,\rho _0,\rho }\). Since \(\mu _0\) is normalized so that it projects to a probability measure on \(X_0\), also \({\widetilde{\mu }}_{0,\rho _0,\rho }\) is a probability measure. Here \({\widetilde{\mu }}_{0,\rho _0,\rho }\) is well defined because of the \(\Gamma _0\)-invariance of \(\nu _{\rho _0,\rho }\). A random element \(\zeta \) in \({\mathcal {X}}_{\varvec{0}}\) defines a random product measure \((\varphi ,\Xi _0)=\varkappa (\zeta )\) in \({\mathcal {M}}(Y)\times {\mathcal {M}}({\mathbb {R}}^d\times Y)\), where \(\varphi \) is a point mass and \(\Xi _0\) a point process.
Lemma 3.5
For \(D\in {\mathscr {B}}(Y\times {\mathbb {R}}^d\times Y)\),
Proof
It is sufficient to consider \(D=B_0\times A\times B\) with \(A\in {\mathscr {B}}({\mathbb {R}}^d)\) and \(B_0,B\in {\mathscr {B}}(Y)\). Since the \(\eta ({\varvec{m}})\), \(\eta ({\varvec{0}})\) are independent with law \(\rho \) and \(\rho _0\) respectively, we have \(\Xi D= \rho _0 (B_0)\Theta _0 (A) \rho (B)\). The expectation is \({{\mathrm{\mathbb {E}}}}\Xi D= \rho _0 (B_0){{\mathrm{\mathbb {E}}}}(\Theta _0 A) \rho (B)\), and the claim follows from Siegel’s formula \({{\mathrm{\mathbb {E}}}}\Theta _0 A={{\mathrm{Leb}}}A\). \(\square \)
4 Spherical averages in the space of marked lattices: convergence on average
Let \(t\in \mathbb {R}\), \(M\in G_0\), \({\varvec{\xi }}\in {\mathbb {R}}^d\), \(\omega \in \Omega \), \(U\subset {\mathbb {R}}^{d-1}\) a bounded set with measure zero boundary (as in Sect. 2), \(\lambda \) an absolutely continuous Borel probability measure on U, and \(\nu \) a probability measure on \(\Omega \) defined by the random field \(\eta \).
We define the Borel probability measures \(P_t^\omega =P_t^{({\varvec{\xi }},M,\omega ,\lambda )}\) and \(Q_t=Q_t^{({\varvec{\xi }},M,\nu ,\lambda )}\) on \({\mathcal {X}}_{\varvec{\xi }}\) by
for bounded continuous functions \(f:{\mathcal {X}}_{\varvec{\xi }}\rightarrow {\mathbb {R}}\). The principal result of this paper is that \(P_t^\omega \) converges weakly to \({\widetilde{\mu }}_{{\varvec{\xi }},\rho }\) (if \({\varvec{\xi }}\notin {\mathbb {Z}}^d\)) or \({\widetilde{\mu }}_{0,\rho _0,\rho }\) (if \({\varvec{\xi }}\in {\mathbb {Z}}^d\)) for \(\nu \)-almost every \(\omega \) (Theorem 5.1). We will first prove this fact for the averaged \(Q_t\).
Theorem 4.1
Assume the random field \(\eta \) is mixing of all orders with asymptotic distribution \(\rho \). Then, for \(t\rightarrow \infty \),
where \(\rho _0\) is the law of \(\eta (-{\varvec{\xi }})\).
Let \(\zeta _t\) be the random element distributed according to \(Q_t\), and \(\zeta \) according to \({\widetilde{\mu }}_{{\varvec{\xi }},\rho }\). Theorem 4.1 \(({\varvec{\xi }}\notin {\mathbb {Z}}^d)\) can then be rephrased as \(\zeta _t \,\,\buildrel \mathrm{d}\over \longrightarrow \,\,\zeta \). Similarly, for \({\varvec{\xi }}\in {\mathbb {Z}}^d\), let \(\zeta _t\) be the random element distributed according to \(Q_t\), and \(\zeta \) according to \({\widetilde{\mu }}_{0,\rho _0,\rho }\). Theorem 4.1 \(({\varvec{\xi }}\in {\mathbb {Z}}^d)\) can then be expressed as well as \(\zeta _t \,\,\buildrel \mathrm{d}\over \longrightarrow \,\,\zeta \). In view of Proposition 2.2 and the continuous mapping theorem [13, Theorem 4.27], this is equivalent to the following convergence in distribution for the random measures \(\Xi _t=\varkappa (\zeta _t)\) and \(\Xi =\varkappa (\zeta ) ({\varvec{\xi }}\notin {\mathbb {Z}}^d)\), \((\varphi _t,\Xi _{0,t})=\varkappa _0(\zeta _t)\) and \((\varphi ,\Xi _0)=\varkappa _0(\zeta ) ({\varvec{\xi }}\in {\mathbb {Z}}^d)\).
Theorem 4.2
Assume \(\eta \) is mixing of all orders with asymptotic distribution \(\rho \). Then, for \(t\rightarrow \infty \),
Theorem 4.2 (and hence Theorem 4.1) follows from the convergence of finite-dimensional distributions by [13, Theorem 16.16] stated in the following propositions.
Proposition 4.3
Let \({\varvec{\xi }}\notin {\mathbb {Z}}^d\), and assume \(\eta \) is mixing of all orders with asymptotic distribution \(\rho \). Let \(n\in {\mathbb {N}}\), \(D_1,\ldots ,D_n\in {\mathscr {B}}({\mathbb {R}}^d\times Y)\) bounded with \(\Xi \partial D_i = 0\) almost surely for all i. Then, for \(t\rightarrow \infty \),
Proposition 4.4
Let \({\varvec{\xi }}\in {\mathbb {Z}}^d\), and assume \(\eta \) is mixing of all orders with asymptotic distribution \(\rho \). Let \(n\in {\mathbb {N}}\), \(D_1,\ldots ,D_n\in {\mathscr {B}}({\mathbb {R}}^d\times Y)\) bounded with \(\Xi _0\partial D_i = 0\) almost surely for all i, and \(B_0\in {\mathscr {B}}(Y)\) with \(\varphi \partial B_0=0\) almost surely. Then, for \(t\rightarrow \infty \),
Proof of Proposition 4.3
It is sufficient to consider test sets of the form \(D_i=A_i\times B_i\) with \(A_i\in {\mathscr {B}}({\mathbb {R}}^d)\) bounded and \(B_i\in {\mathscr {B}}(Y)\) such that \(\Xi \partial (A_i\times B_i)=0\) almost surely. In view of Lemma 3.4 the latter is equivalent to \(({{\mathrm{Leb}}}\times \rho )\partial (A_i\times B_i)=0\). We also assume without loss of generality that \(A_i\) are pairwise disjoint.
Corollary 2.4, Lemma 2.5 and the Chebyshev inequality imply that for every bounded \(D_0=A_0\times B_0\) we have
Hence sets \(D_0=A_0\times B_0\) where the closure of \(A_0\) has small Lebesgue measure have small probability, and we can thus remove such sets from the \(D_i\). This explains why, without loss of generality, we may assume from now on that the \(A_i\) are convex and that the hyperplane \(\{x_1=0\}\) does not intersect the closure \(\overline{A}\) of \(A:=\cup _{i=1}^n A_i\). Set
and write \({\varvec{q}}={\varvec{m}}(\mathbbm {1},{\varvec{\xi }})M E({\varvec{u}})\Phi ^t\in {\mathcal {L}}_{t,{\varvec{u}}}\) with \({\varvec{m}}\in {\mathbb {Z}}^d\) uniquely determined by \({\varvec{q}}\). Writing \({\varvec{e}}_1=(1,0,\ldots ,0)\) for the first standard basis vector in \(\mathbb {R}^d\), we have
and hence for some constants \(c_M>0\), \(c_{A,M}>0\) (depending only on M resp. A and M)
uniformly for all \({\varvec{q}}\in A\), \(t\geqslant 0\).
For a small parameter \(\varepsilon >0\) to be chosen later write \(U=U_1^{(\varepsilon )} \cup U_2^{(\varepsilon )}\), where
and \(U_2^{(\varepsilon )} = U\setminus U_1^{(\varepsilon )}.\) The set \(U_2^{(\varepsilon )}\) comprises directions corresponding to lattice points \({\varvec{m}}\in {\mathbb {Z}}^d\) that are \(\varepsilon e^{(d-1)t}\)-separated. That is, for \({\varvec{q}}_1={\varvec{m}}_1(\mathbbm {1},{\varvec{\xi }})M E({\varvec{u}})\Phi ^t\) and \({\varvec{q}}_2={\varvec{m}}_2(\mathbbm {1},{\varvec{\xi }})M E({\varvec{u}})\Phi ^t\) with \({\varvec{u}}\in U_2^{(\varepsilon )}\), we have
and hence
We will use the higher-order mixing property to show that markings at such points become independent. The set \(U_1^{(\varepsilon )}\) includes directions in which there are some lattice points that are close. We will show that the measure of such directions tends to zero as \(\varepsilon \rightarrow 0\).
For non-negative integers \(r_1,\ldots , r_n\),
We deal with the first term by writing
Split the summation into terms with \(\max _{i} l_i \leqslant L\) and \(\max _{i} l_i > L\) for some large L. For the latter,
and by Corollary 2.4 there is \(t_0(L,A)\) such that for all \(t>t_0(L,A)\),
where the last bound follows from Lemma 2.6. We conclude that, for all \(L\geqslant 1\),
Let us now turn to the remaining term
The only terms which contribute are those with \(l_i\geqslant r_i\). We have
where \(J_i={\mathcal {L}}_{t,{\varvec{u}}}\cap A_i\). By the choice of \(U_2^{(\varepsilon )}\), all contributing lattice points are \(c_M\varepsilon e^{(d-1)t}\)-separated, and so, by mixing of all orders,
where the sum is over all subsets S of \(J_i\) of cardinality \(r_i\). There are \(\genfrac(){0.0pt}1{l_i}{r_i}\) such subsets. Again by the choice of \(U_2^{(\varepsilon )}\), all contributing lattice points are furthermore at distance at least \(c_{A,M} e^{(d-1)t}\) from \({\varvec{\xi }}\). Since \(\eta \) has the asymptotic distribution \(\rho \), we therefore have
where \(p_i = \rho (B_i)\). Now
and thus
where the implied constants are l-independent. Therefore, using Corollary 2.4,
where
As observed earlier,
by Lemma 2.6. This yields
By the definition of \(\Xi \),
Combining the estimates (4.20) and (4.31) yields for \(L\rightarrow \infty \),
Here \(\varepsilon >0\) is arbitrary. In view of (4.14) and (4.33), what remains to be shown is that \(E^{(\varepsilon )}\rightarrow 0\) as \(\varepsilon \rightarrow 0\). To this end, notice that
Since A is bounded, the number of non-zero terms in this sum is \(O(1/\varepsilon )\), where the implied constant depends only on A (not on t). Taking the limit \(t\rightarrow \infty \) yields (Corollary 2.4)
Because we have assumed that the closure of A does not meet the hyperplane \(\{x_1=0\}\), for each \(k\geqslant 0\) the set \(A \cap \big ( [k\varepsilon ,k\varepsilon +2\varepsilon ] \times \mathbb {R}^{d-1}\big )\) is contained in the cylinder
form some \(c_1>0\), \(c_2>c_1+2\varepsilon \), and C sufficiently large in terms of A. (The case of negative k is analogous.) Therefore, when \(d=2\) and \({\varvec{\xi }}\in \mathbb {Q}^2\), we have [17, Lemma 7.12]
and so \(E^{(\varepsilon )} = O( \varepsilon \log \varepsilon )\rightarrow 0\) as \(\varepsilon \rightarrow 0\). In all other cases we have (use [17, Lemmas 7.12] for \({\varvec{\xi }}\in {\mathbb {Q}}^d\), \(d\geqslant 3\), and [17, Lemmas 7.13] for \({\varvec{\xi }}\notin {\mathbb {Q}}^d\), \(d\geqslant 2\))
that is \(E^{(\varepsilon )} =O (\varepsilon )\rightarrow 0\) as \(\varepsilon \rightarrow 0\). \(\square \)
Proof of Proposition 4.4
The proof is almost the same as that of Proposition 4.3. We have that \(\Xi _{0,t}\) is a random point process on \(\mathbb {R}^d\) that is jointly measurable with a random variable on Y whose marginal is \(\varphi _t\). We follow the steps of the previous proof until (4.14). For \(r_i \in \mathbb N\cup \{0\}\), \(i\geqslant 1\), we have
The next substantive modification is in the application of mixing of order nL in (4.21), which becomes
Note that here \({{\mathrm{\mathbb {P}}}}(\varphi _t B_0 = 1) = {{\mathrm{\mathbb {P}}}}(\varphi B_0 = 1) = \rho _0(B_0)\). The remainder of the proof runs parallel to that of Proposition 4.3. \(\square \)
5 Spherical averages in the space of marked lattices: almost sure convergence
Let us now turn to the main result of this paper. We say the random field \(\eta \) is slog-mixing (slog stands for strongly super-logarithmic), if for every \(\delta >0\)
This holds for instance when
for all \(s\geqslant 2\), with positive constants C, \(\varepsilon \).
Main Theorem 5.1
Fix \({\varvec{\xi }}\in {\mathbb {R}}^d\) and \(M\in G_0\). Assume the random field \(\eta \) is slog-mixing with asymptotic distribution \(\rho \). Then there is a set \(\Omega _0\subset \Omega \) with \(\nu (\Omega _0)=1\), such that for every \(\omega \in \Omega _0\) and every a.c. Borel probability measure \(\lambda \) on U,
as \(t\rightarrow \infty \), where \(\rho _0=\delta _{\omega (-{\varvec{\xi }})}\).
Let \(\zeta _t^\omega \) be the random element distributed according to \(P_t^\omega \), and \(\zeta \) according to \({\widetilde{\mu }}_{{\varvec{\xi }},\rho }\). Theorem 5.1 \(({\varvec{\xi }}\notin {\mathbb {Z}}^d)\) says that \(\zeta _t^\omega \,\,\buildrel \mathrm{d}\over \longrightarrow \,\,\zeta \) for \(\nu \)-almost every \(\omega \). Similarly for \({\varvec{\xi }}\in {\mathbb {Z}}^d\), let \(\zeta _t^\omega \) be the random element distributed according to \(P_t^\omega \), and \(\zeta \) according to \({\widetilde{\mu }}_{0,\rho _0,\rho }\) where \(\rho _0=\delta _{\omega (-{\varvec{\xi }})}\). Theorem 5.1 \(({\varvec{\xi }}\in {\mathbb {Z}}^d)\) can then be expressed as well as \(\zeta _t^\omega \,\,\buildrel \mathrm{d}\over \longrightarrow \,\,\zeta ^\omega \) for \(\nu \)-almost-every \(\omega \). (The \(\omega \)-dependence of \(\zeta ^\omega \) is only through \(\rho _0\).) Again, in view of Proposition 2.2 and the continuous mapping theorem [13, Theorem 4.27], this is equivalent to the following convergence in distribution for the random measures \(\Xi _t^\omega =\varkappa (\zeta _t^\omega )\) and \(\Xi =\varkappa (\zeta )\) (\({\varvec{\xi }}\notin {\mathbb {Z}}^d\)), \((\varphi _t^\omega ,\Xi _{0,t}^\omega )=\varkappa _0(\zeta _t^\omega )\), \((\varphi ^\omega ,\Xi _0)=\varkappa _0(\zeta ^\omega )\) (\({\varvec{\xi }}\in {\mathbb {Z}}^d\)). Note that here \(\varphi _t^\omega =\varphi ^\omega =\delta _{\omega (-{\varvec{\xi }})}\). Thus, if \(\omega \) is fixed, then \(\varphi _t^\omega \) is deterministic and independent of t, and we may state the convergence solely for \( \Xi _{0,t}^\omega \) rather than the joint distribution \((\varphi _t^\omega , \Xi _{0,t}^\omega )\) used in the case of random \(\omega \) (Proposition 4.2).
Theorem 5.2
Under the assumptions of Theorem 5.1, for every \(\omega \in \Omega _0\) and every a.c. Borel probability measure \(\lambda \) on U,
Again by [13, Theorem 16.16], Theorem 5.2 (and hence Theorem 5.1) follows from the convergence of finite-dimensional distributions:
Proposition 5.3
Under the assumptions of Theorem 5.1 with \({\varvec{\xi }}\notin {\mathbb {Z}}^d\), for every \(\omega \in \Omega _0\), every a.c. Borel probability measure \(\lambda \) on U, every \(n\in {\mathbb {N}}\) and all \(D_1,\ldots ,D_n\in {\mathscr {B}}({\mathbb {R}}^d\times Y)\) that are bounded with \(\Xi \partial D_i = 0\) almost surely for all i,
Proposition 5.4
Under the assumptions of Theorem 5.1 with \({\varvec{\xi }}\in {\mathbb {Z}}^d\), for every \(\omega \in \Omega _0\), every a.c. Borel probability measure \(\lambda \) on U, every \(n\in {\mathbb {N}}\) and all \(D_1,\ldots ,D_n\in {\mathscr {B}}({\mathbb {R}}^d\times Y)\) that are bounded with \(\Xi _0\partial D_i = 0\) almost surely for all i,
The proof of these two propositions will require the following lemma. For each \(\zeta >0\), define \({\mathscr {C}}_\zeta \subset {\mathscr {B}}({\mathbb {R}}^d\times Y)\) as the collection of sets \(D=A\times B\) with the following properties:
-
(i)
\(A\in {\mathscr {B}}({\mathbb {R}}^d)\) is convex and contained in the ball of radius \(1/\zeta \) around the origin,
-
(ii)
\(B\in {\mathscr {B}}(Y)\) such that \(({{\mathrm{Leb}}}\times \rho )\partial (A\times B)=0\),
-
(iii)
\(([-\zeta , \zeta ]\times \mathbb {R}^{d-1}) \cap A = \varnothing \).
Lemma 5.5
Given \(\varepsilon >0\), \(\zeta <\infty \), there are constants \(s_0\), \(t_0\) such that for all \(t\geqslant t_0\), \(|s|\leqslant s_0\), \(\omega \in \Omega \), and every \(D\in {\mathscr {C}}_\zeta \) (in fact we only require property (i) in the definition of \({\mathscr {C}}_\zeta \)),
Proof
We have
and therefore
For the latter we have
by Corollary 2.4 and Lemma 2.5. The claim follows from the fact that
uniformly for any convex A contained in a fixed ball. The proof for \(\Xi _{0,t}^\omega \) is identical. \(\square \)
Proof of Proposition 5.3
We have
where \(\Xi _t\) is the process considered in Proposition 4.3. Our first task is to show that
decays sufficiently fast for large t, uniformly for all a.c. Borel probability measures \(\lambda \) on U and all \(D_1,\ldots ,D_n\in {\mathscr {C}}_\zeta \) (with n arbitrary but fixed), thus allowing an application of the Borel-Cantelli lemma to establish almost sure convergence.
Let \(\Xi _{t,1}^\omega \), \(\Xi _{t,2}^\omega \) be two independent copies of \(\Xi _t^\omega \). The corresponding rotation parameter \({\varvec{u}}\) is denoted by \({\varvec{u}}_1\), \({\varvec{u}}_2\), respectively, which are independent and distributed according to \(\lambda \). Then
We condition on \({\varvec{e}}_1 E({\varvec{u}}_1)^{-1}\), \(\pm {\varvec{e}}_1 E({\varvec{u}}_2)^{-1}\) being close or not. Let \(\theta _0 \leqslant 1\) be small to be chosen later depending on t. If \(\min _\pm \Vert {\varvec{e}}_1 E({\varvec{u}}_1)^{-1} \pm {\varvec{e}}_1 E({\varvec{u}}_2)^{-1}\Vert \leqslant \theta _0\), then we estimate trivially to get
for \(\theta _0\) sufficiently small, since \(\widetilde{E}(U)\) is contained in a hemisphere (recall the assumptions following (2.12)). Let \(\overline{M}\) be the Lipschitz constant of the inverse of the map \(U\rightarrow \widetilde{E}(U)\subset {\text {S}}^{d-1}_1\), \({\varvec{u}}\mapsto {\varvec{e}}_1 E({\varvec{u}})^{-1}\). Then, using the fact that \(\lambda \) has density \(\lambda '\in L^1(U,d{\varvec{u}})\), we bound (5.16) by
for any \(K\geqslant 1\), where the implied constant depends only on U. If we pick \(K = \theta _0^{-(d-1)/3}\), we get the bound \(\theta _0^{(d-1)/3}\) for this regime. Consider the complementary case, \(\Vert {\varvec{e}}_1 E({\varvec{u}}_1)^{-1} \pm {\varvec{e}}_1 E({\varvec{u}}_2)^{-1}\Vert > \theta _0\). Recall that for every i, the closure of \(A_i\) does not intersect a \(\zeta \)-neighborhood of the hyperplane \(\{x_1=0\}\), and \(A_i\) is contained in a ball of radius \(1/\zeta \). This implies that the set \(A_i \Phi ^{-t} E({\varvec{u}})^{-1}\) asymptotically aligns in direction \(\pm {\varvec{e}}_1 E({\varvec{u}})^{-1}\), avoiding a \(\mathrm {e}^{(d-1)t}\)-neighborhood of the origin. More precisely, there is a constant \(C_\zeta >0\) such that
for all \({\varvec{q}}_1\in A_i\), \({\varvec{q}}_2\in A_j\) and all i, j. Hence for \({\varvec{m}}_1,{\varvec{m}}_2\) defined by
we have
This shows that the lattice points \({\varvec{m}}_1,{\varvec{m}}_2\in {\mathbb {Z}}^d\) that contribute to \({\varvec{u}}_1\) and \({\varvec{u}}_2\) respectively, are at distance at least \(c_{M} C_\zeta \theta _0 e^{(d-1)t}\) apart. Thus, by strong mixing,
where \(\Xi _{t,1}\), \(\Xi _{t,2}\) are independent copies of \(\Xi _t\), and the implicit constant in the error term is independent of the choice of \(\lambda \) and of \(D_1,\ldots ,D_n\in {\mathscr {C}}_\zeta \). Estimate (5.19) yields
Altogether we therefore have
where the supremum is taken over all a.c. \(\lambda \) and all \(D_1,\ldots ,D_n\in {\mathscr {C}}_\zeta \). If we choose \(\theta _0 = e^{-\gamma t}\) for any \(\gamma \in (0,d-1)\), we get
for every \(\delta >0\) by the slog-mixing assumption (5.1) and monotonicity of \(\alpha \). All of the above estimates are uniform in \(\lambda \) and \(D_1,\ldots ,D_n\in {\mathscr {C}}_\zeta \).
From the Borel–Cantelli Lemma we conclude that, for every \(\varepsilon >0\),
Now choose \(\delta >0\) and \(k_0\) such that for all \(k\geqslant k_0\), \(0\leqslant s < \delta \),
This is possible in view of Lemma 5.5, since
This shows that (set \(t=k\delta +s\))
By Proposition 4.3, for every a.c. \(\lambda \) and all \(D_1,\ldots ,D_n\in {\mathscr {C}}_\zeta \),
Hence (5.39) implies that there is a set \(\Omega _{\zeta ,n}\) of full measure, such that for every \(\omega \in \Omega _{\zeta ,n}\), all a.c. \(\lambda \) and all \(D_1,\ldots ,D_n\in {\mathscr {C}}_\zeta \),
Corollary 2.4, Lemma 2.5 and Chebyshev’s inequality imply that for every \(D_0=A_0\times B_0\) we have
for all \(\omega \in \Omega \). That is, the probability of having at least one point in a small-measure set is small, which shows that (5.41) in fact holds for all sets of the form \(D_i=A_i\times B_i\) with \(A_i\in {\mathscr {B}}({\mathbb {R}}^d)\) bounded and \(B_i\in {\mathscr {B}}(Y)\) such that \(({{\mathrm{Leb}}}\times \rho )\partial (A_i\times B_i)=0\), provided
The convergence in (5.41) holds for all n for a given \(\omega \), if
which still is a set of full measure. The extension of (5.41) from product sets \(A_i\times B_i\) to general sets \(D_i\) follows from a standard approximation argument. \(\square \)
Proof of Proposition 5.4
This is identical to the proof of Proposition 5.3, with Proposition 4.3 replaced by Proposition 4.4. \(\square \)
We conclude this section with two corollaries of Theorem 5.1.
Corollary 5.6
Under the assumptions of Theorem 5.1, for every \(\omega \in \Omega _0\), every a.c. \(\lambda \), and every bounded continuous \(f:{\mathbb {R}}^{d-1} \times {\mathcal {X}}_{\varvec{\xi }}\rightarrow {\mathbb {R}}\),
where \(\rho _0=\delta _{\omega (-{\varvec{\xi }})}\).
Proof
This follows from Theorem 5.1 by the same argument as in the proof of Theorem 5.3 in [17]. \(\square \)
Let us assume that there is a continuous map \(\varphi :U\times \Omega \rightarrow \Omega \). Then the following is an immediate consequence of Corollary 5.6.
Corollary 5.7
Under the assumptions of Theorem 5.1, for every \(\omega \in \Omega _0\), every a.c. \(\lambda \), and every bounded continuous \(f:{\mathbb {R}}^{d-1} \times {\mathcal {X}}_{\varvec{\xi }}\rightarrow {\mathbb {R}}\),
where \(\rho _0=\delta _{\omega (-{\varvec{\xi }})}\).
Proof
Apply Corollary 5.6 with the test functions \(\tilde{f}\) defined by
\(\square \)
6 Random defects
Spherical averages were used in [17] and [19] to establish the limit distribution for the free path length in crystals and quasicrystals, respectively. The plan for the remainder of this paper is to explain how spherical averages on marked lattices can be exploited to yield the path length distribution for crystals with random defects. The idea is to start with a perfect crystal, whose scatterers are located at the vertices of an affine Euclidean lattice \({\mathcal {L}}=\mathbb {Z}^d (\mathbbm {1},{\varvec{\xi }})M\), and then remove or shift each lattice point with a given probability. This can be encoded by a marking of \({\mathcal {L}}\) as follows. The set of marks is \(Y=\{0,1\} \times {\mathbb {R}}^d\), where the first coordinate describes the absence or presence of a lattice point, and the second its relative shift measured in units of \(r=\mathrm {e}^{-t}\). The corresponding marking is denoted by \(\omega =(a,{\varvec{z}})\) with \(a:{\mathbb {Z}}^d \rightarrow \{0,1\}\) and \({\varvec{z}}:{\mathbb {Z}}^d \rightarrow {\mathbb {R}}^d\). The defect affine lattice is thus
In the case when \({\varvec{\xi }}\in {\mathbb {Z}}^d\), it is natural to shift the above point set by \(-r{\varvec{z}}(-{\varvec{\xi }})\) so that the shifted set contains the origin. To unify notation, let us therefore define the field \({\varvec{z}}_{\varvec{\xi }}\) by
In fact, for our application to the Lorentz gas, it will be convenient to shift the point set by a more general vector \(r{\varvec{\beta }}\), where \({\varvec{\beta }}\) is a fixed bounded continuous function \(U\rightarrow {\mathbb {R}}^d\); we denote the shifted set (for all \({\varvec{\xi }}\in {\mathbb {R}}^d\)) by
As in the case of lattices (4.8), we are interested in the rotated-stretched point set \({\mathcal {P}}_{t,{\varvec{u}}}=\widetilde{{\mathcal {P}}}_{r,{\varvec{u}}} E({\varvec{u}})\Phi ^t\), which reads explicitly (for \(r=\mathrm {e}^{-t}\))
where \((\,\cdot \,)_\perp \) is the orthogonal projection onto the hyperplane perpendicular to \({\varvec{e}}_1\).
We map the marked affine lattice (viewed as an element in \({\mathcal {X}}\)) to a defect lattice (viewed as an element in \({\mathcal {M}}({\mathbb {R}}^d)\)) by
where \(\omega =(a,{\varvec{z}})\). The motivation for this definition is as follows. Define the family of maps \(J_t:\Omega \rightarrow \Omega \) by
and (for later use)
Then
and, for \({\varvec{\xi }}\in {\mathbb {Z}}^d\),
We will first discuss the relevant spherical averages in \({\mathcal {X}}_{\varvec{\xi }}\), and then show they map to the above point processes.
Theorem 6.1
Assume \(\eta \) is slog-mixing with asymptotic distribution \(\rho \), and \(\rho \) has compact support. Fix \(M\in G_0\) and \({\varvec{\xi }}\in {\mathbb {R}}^d\). Then there exists a set \(\Omega _0\subset \Omega \) with \(\nu (\Omega _0)=1\), such that for every \(\omega =(a,{\varvec{z}})\in \Omega _0\), every a.c. \(\lambda \) and every bounded continuous \(f:{\mathbb {R}}^{d-1} \times {\mathcal {X}}_{\varvec{\xi }}\rightarrow {\mathbb {R}}\),
where \(\rho _0=\delta _{\omega (-{\varvec{\xi }})}\).
Proof
Since \(\rho \) has compact support and \({\varvec{\beta }}\) is bounded,
and hence \(J_t(a,[{\varvec{z}}_{\varvec{\xi }}-{\varvec{\beta }}({\varvec{u}})] E({\varvec{u}}))({\varvec{m}})\rightarrow J_\infty (a,[{\varvec{z}}_{\varvec{\xi }}-{\varvec{\beta }}({\varvec{u}})] E({\varvec{u}}))({\varvec{m}})\) uniformly in \({\varvec{u}}\in U\), \({\varvec{m}}\in {\mathbb {Z}}^d\). The claim now follows from Corollary 5.7. \(\square \)
The following is the key to translate the above convergence into the setting of point processes.
Lemma 6.2
The maps \(\sigma \) and \(\sigma _0\) are continuous.
Proof
The proof is similar to that of Proposition 2.2; we sketch it in the case of \(\sigma \).
We need to show that \(x_j\rightarrow x \in {\mathcal {X}}\) implies that, for every \(f\in C_c(\mathbb {R}^d)\),
Since f is of compact support, the sums above are finite, and we can rewrite the left hand side as
which is another finite sum. In particular, for all \({\varvec{m}}\) in the support, we have that \(a_j({\varvec{m}}) = a({\varvec{m}})\) and \(|{\varvec{z}}_j({\varvec{m}}) - {\varvec{z}}({\varvec{m}})|<\varepsilon \) once \(j\geqslant j_0\). The statement (6.13) now follows from continuity of f. \(\square \)
For \({\varvec{u}}\) randomly distributed according to \(\lambda \), we define the random point processes
for \({\varvec{\xi }}\notin {\mathbb {Z}}^d\) and \({\varvec{\xi }}\in {\mathbb {Z}}^d\), respectively. If \({\varvec{\xi }}\notin {\mathbb {Z}}^d\), we furthermore set
with \((g,(a,{\varvec{z}}))\) distributed according to \({\widetilde{\mu }}_{{\varvec{\xi }},\rho }\) and \({\varvec{u}}\) distributed according to \(\lambda \). That is, \(\widetilde{\Xi }\) is a random affine lattice \({\mathbb {Z}}^d g\) distributed according to \(\mu \), where each lattice point is removed, or shifted in the hyperplane \(V_\perp =\{0\}\times {\mathbb {R}}^{d-1}\), according to the push-forward of the probability measure \(\lambda \times \rho \) on \(U\times \{0,1\}\times {\mathbb {R}}^d\) under the map \(({\varvec{u}},a,{\varvec{z}})\mapsto (a,({\varvec{z}}E({\varvec{u}}))_\perp )\). If \(\rho \) is rotation-invariant, then this measure is independent of \(\lambda \). In the case \({\varvec{\xi }}\in {\mathbb {Z}}^d\), we put
with \((g,(a,{\varvec{z}}))\) distributed according to \({\widetilde{\mu }}_{0,\rho _0,\rho }\) and \({\varvec{u}}\) distributed according to \(\lambda \). This means that \(\widetilde{\Xi }_0\) is a random lattice \({\mathbb {Z}}^d g\setminus \{{\varvec{0}}\}\) distributed according to \(\mu _0\), where each lattice point is removed, or shifted in the hyperplane \(V_\perp =\{0\}\times {\mathbb {R}}^{d-1}\), according to the push-forward of the probability measure \(\lambda \times \rho \) on \(U\times \{0,1\}\times {\mathbb {R}}^d\) under the map
This measure depends on \(\lambda \) even if \(\rho \) is rotation invariant.
Theorem 6.1 implies via Lemma 6.2 and the continuous mapping theorem the following convergence in distribution.
Corollary 6.3
Under the conditions of Theorem 6.1, for every \(\omega \in \Omega _0\) and every a.c. \(\lambda \),
The following Siegel–Veech type formula allows us to simplify the assumptions on the test sets for the finite-dimensional distribution. Set
Lemma 6.4
For \(A\in {\mathscr {B}}({\mathbb {R}}^d)\),
Proof
For \(f\in C_c({\mathbb {R}}^d)\),
By Lemma 3.4, we have then
which, after translating \({\varvec{x}}\) by \(-([{\varvec{y}}-{\varvec{\beta }}({\varvec{u}})]E({\varvec{u}}))_\perp )\), yields
The proof for \(\widetilde{\Xi }_0\) is identical. \(\square \)
The following is a direct consequence of Corollary 6.3 and Lemma 6.4.
Corollary 6.5
Assume the conditions of Theorem 6.1. Then, for every \(\omega \in \Omega _0\), every a.c. \(\lambda \), every \(n\in {\mathbb {N}}\) and all \(A_1,\ldots ,A_n\in {\mathscr {B}}({\mathbb {R}}^d)\) that are bounded with \({{\mathrm{Leb}}}\partial A_i = 0\) for all i,
and
Proof
Lemma 6.4 implies that \({{\mathrm{Leb}}}\partial A_i = 0\) implies \(\widetilde{\Xi }\partial A_i = 0\) almost surely and \(\widetilde{\Xi }_0\partial A_i = 0\) almost surely, and the claim follows from [13, Theorem 16.16]. \(\square \)
7 Free path lengths in the Lorentz gas
For a given point set \({\mathcal {P}}\subset {\mathbb {R}}^d\), center an open ball \({\mathcal {B}}_r^d+{\varvec{y}}\) of radius r at each of the points \({\varvec{y}}\) in \({\mathcal {P}}\). The Lorentz gas describes the dynamics of point particle in this array of balls, where the particle moves with unit velocity until it hits a ball, where it is scattered according to a given scattering map. The configuration space for the dynamics is thus \({\mathcal {K}}_r={\mathbb {R}}^d\setminus ({\mathcal {B}}_r^d+{\mathcal {P}})\). Given the initial position \({\varvec{q}}\in {\mathcal {K}}_r\) and velocity \({\varvec{v}}\in {\text {S}}_1^{d-1}\), the free path length is defined as the travel distance until the next collision,
The distribution of the free path length is well understood for random [2], periodic [1, 5, 17] and quasiperiodic [19, 20] scatterer configurations. We will here consider the periodic Lorentz gas with random defects introduced in the previous section, where the scatterers are placed at the defect lattice
Note that the papers [4, 23] discuss the convergence of a defect periodic Lorentz gas to a random flight process governed by the linear Boltzmann equation in the limit when the removal probability of a scatterer tends to one. In this case the free path length distribution is exponential, whereas for a fixed removal probability \(<1\) the path length distribution has a power-law tail; cf. (7.13).
As in [17], we will consider more general initial conditions, which for instance permit us to launch a particle from the boundary of a scatterer (which is moving as \(r\rightarrow 0\)). Let \({\varvec{\beta }}:{\text {S}}_1^{d-1}\rightarrow {\mathbb {R}}^d\) be a continuous function, and consider the initial condition \({\varvec{q}}+r{\varvec{\beta }}({\varvec{v}})\). If \({\varvec{q}}\in {\mathbb {Z}}^d M\) and the initial condition is thus very near (within distance O(r)) to a scatterer, we will avoid initial conditions inside the scatterer, or those that immediately hit the scatterer, by assuming that \({\varvec{\beta }}\) is such that the ray \({\varvec{\beta }}({\varvec{v}})+\mathbb {R}_{>0}{\varvec{v}}\) lies completely outside \({\mathcal {B}}_1^d\), for each \({\varvec{v}}\in {\text {S}}_1^{d-1}\).
The following theorem proves the existence of the free path length distribution for (a) random initial data \(({\varvec{q}}+r{\varvec{\beta }}({\varvec{v}}),{\varvec{v}})\) for \({\varvec{q}}\notin {\mathbb {Z}}^d M\) fixed, and \({\varvec{v}}\) random with law \(\lambda \), and (b) random initial data \(({\varvec{q}}+r{\varvec{\beta }}({\varvec{v}})+r{\varvec{z}}({\varvec{q}}M^{-1}),{\varvec{v}})\) for \({\varvec{q}}\in {\mathbb {Z}}^d M\) fixed, and \({\varvec{v}}\) random with law \(\lambda \).
Theorem 7.1
Assume \(\eta \) is slog-mixing with asymptotic distribution \(\rho \), and \(\rho \) has compact support. Fix \(M\in G_0\) and \({\varvec{q}}\in {\mathbb {R}}^d\). There exist continuous, non-increasing functions \(F_s:{\mathbb {R}}_{\geqslant 0} \rightarrow \mathbb {R}\) with \(F_s(0)=1\) (\(s\in {\mathbb {Z}}_{\geqslant 0}\)) and a set \(\Omega _0\subset \Omega \) with \(\nu (\Omega _0)=1\), such that the following hold for every \(T\geqslant 0\), every \((a,{\varvec{z}})\in \Omega _0\) and every absolutely continuous Borel probability measure \(\lambda \) on \({\text {S}}_1^{d-1}\):
-
(i)
If \({\varvec{q}}\in {\mathbb {R}}^d\setminus {\mathbb {Q}}^d M\), then
$$\begin{aligned} \lim _{r\rightarrow 0} \lambda \left\{ {\varvec{v}}\in {\text {S}}_1^{d-1} : r^{d-1} \tau \left( {\varvec{q}}+r{\varvec{\beta }}({\varvec{v}}),{\varvec{v}};r\right) \geqslant T \right\} = F_0(T). \end{aligned}$$(7.3) -
(ii)
If \({\varvec{q}}=s^{-1}{\varvec{m}}M\) with \(s\in {\mathbb {Z}}_{\geqslant 2}\), \({\varvec{m}}\in {\mathbb {Z}}^d\), \(\gcd ({\varvec{m}},s)=1\), then
$$\begin{aligned} \lim _{r\rightarrow 0} \lambda \left\{ {\varvec{v}}\in {\text {S}}_1^{d-1} : r^{d-1} \tau \left( {\varvec{q}}+r{\varvec{\beta }}({\varvec{v}}),{\varvec{v}};r\right) \geqslant T \right\} = F_s(T). \end{aligned}$$(7.4) -
(iii)
If \({\varvec{q}}\in {\mathbb {Z}}^d M\), then
$$\begin{aligned} \lim _{r\rightarrow 0} \lambda \left\{ {\varvec{v}}\in {\text {S}}_1^{d-1} : r^{d-1} \tau \left( {\varvec{q}}+r{\varvec{\beta }}({\varvec{v}})+r{\varvec{z}}\left( {\varvec{q}}M^{-1}\right) ,{\varvec{v}};r \right) \geqslant T \right\} = F_1(T) . \end{aligned}$$(7.5)
Proof
The proof follows from Corollary 6.5 in the case of one-dimensional distributions (\(n=1\)) by the same arguments as in [17]. This proves the existence of the limits with
where
Note that the limit process \(\widetilde{\Xi }\) is independent of the choice of \({\varvec{\xi }}\) when \({\varvec{\xi }}\notin {\mathbb {Q}}^d\), and only depends on the denominator of \({\varvec{\xi }}\) when \({\varvec{\xi }}\in {\mathbb {Q}}^d\setminus {\mathbb {Z}}^d\); cf. [17] for a detailed discussion. Furthermore \(\widetilde{\Xi }_0\) is independent of \({\varvec{\xi }}\in {\mathbb {Z}}^d\). \(\square \)
Let \(r_{\max }\) be the infimum over the radii of balls centered at the origin that contain the support of \(\rho (1,\,\cdot \,)\) (which we have assumed to be compact). Then the maximal distance between a point in the random affine lattice \(\Theta \) and its displacement in \(\widetilde{\Xi }\) is \(r_{\max }\). Denote by \(\overline{F}_s\) the corresponding path length distribution
Lemma 7.2
For \(T\geqslant 0\),
Proof
We have
where the last equality follows from the \(G_0\)-invariance of \(\Theta \). \(\square \)
This lemma allows us to obtain lower bounds for the tails of \(F_s(T)\) in terms of the free path length asymptotics derived in [18]. In particular, Theorem 1.13 in that paper implies the power-law lower bound
Note that this bound becomes ineffective in the limit of large \(r_{\max }\). The bound is also consistent with the exponential distribution in the limit of removal probability \(\rightarrow 1\) discussed in [4, 23], if the free path length is measured in units of the mean free path length, which diverges as the removal probability tends to one.
References
Boca, F.P., Zaharescu, A.: The distribution of the free path lengths in the periodic two-dimensional Lorentz gas in the small-scatterer limit. Comm. Math. Phys. 269(2), 425–471 (2007)
Boldrighini, C., Bunimovich, L.A., Sinai, Y.G.: On the Boltzmann equation for the Lorentz gas. J. Stat. Phys 32(3), 477–501 (1983)
Brettschneier, J.: On uniform convergence in ergodic theorems for a class of skew product transformations. Discrete Contin. Dyn. Syst. 29(3), 873–891 (2011)
Caglioti, E., Pulvirenti, M., Ricci, V.: Derivation of a linear Boltzmann equation for a lattice gas. Markov Process. Relat. Fields 6(3), 265–285 (2000)
Caglioti, E., Golse, F.: On the Boltzmann-Grad limit for the two dimensional periodic Lorentz gas. J. Stat. Phys. 141(2), 264–317 (2010)
Einsiedler, M., Ward, T.: Ergodic Theory with a View Towards Number Theory. Graduate Texts in Mathematics, vol. 29. Springer, London (2011)
Eskin, A., McMullen, C.: Mixing, counting, and equidistribution in Lie groups. Duke Math. J. 71, 181–209 (1993)
Eskin, A., Margulis, G., Mozes, S.: Upper bounds and asymptotics in a quantitative version of the Oppenheim conjecture. Ann. Math (2) 147(1), 93–141 (1998)
Eskin, A., Margulis, G., Mozes, S.: Quadratic forms of signature \((2,2)\) and eigenvalue spacings on rectangular 2-tori. Ann. Math. (2) 161(2), 679–725 (2005)
Eskin, A., Marklof, J., Morris, D.W.: Unipotent flows on the space of branched covers of Veech surfaces. Ergodic Theory Dyn. Syst. 26(1), 129–162 (2006)
Eskin, A., Mirzakhani, M.: Invariant and stationary measures for the \(\text{SL} (2,{\mathbb{R}})\) action on moduli space. arXiv:1302.3320, (2013)
Eskin, A., Mirzakhani, M., Mohammadi, A.: Isolation, equidistribution, and orbit closures for the \(\text{ SL } (2,{\mathbb{R}})\) action on Moduli space. Ann. Math. 182(2), 673–721 (2015)
Kallenberg, O.: Foundations of Modern Probability. Probability and its Applications (New York), 2nd edn. Springer, New York (2002)
Ledrappier, F.: Un champ markovien peut être d’entropie nulle et mélangeant. C. R. Acad. Sci. Paris Sér. A-B 287(7), A561–A563 (1978)
Marklof, J.: The \(n\)-point correlations between values of a linear form. Ergodic Theory Dyn. Syst. 20(4), 1127–1172 (2000). With an appendix by Zeév Rudnick
Marklof, J.: Pair correlation densities of inhomogeneous quadratic forms. Ann. Math. (2) 158(2), 419–471 (2003)
Marklof, J., Strömbergsson, A.: The distribution of free path lengths in the periodic Lorentz gas and related lattice point problems. Ann. Math. 172(3), 1949–2033 (2010)
Marklof, J., Strömbergsson, A.: The periodic Lorentz gas in the Boltzmann–Grad limit: asymptotic estimates. Geom. Funct. Anal. 21(3), 560–647 (2011)
Marklof, J., Strömbergsson, A.: Free path lengths in quasicrystals. Commun. Math. Phys. 330(2), 723–755 (2014)
Marklof, J., Strömbergsson, A.: Power-law distributions for the free path length in Lorentz gases. J. Stat. Phys. 155(6), 1072–1086 (2014)
Nevo, A.: Pointwise ergodic theorems for actions of groups. In: Hasselblatt, B., Katok, A. (eds.) Handbook of Dynamical Systems vol. 1B, pp. 871–982. Elsevier B. V., Amsterdam (2006)
Ratner, M.: On Raghunathan’s measure conjecture. Ann. Math. (2) 134(3), 545–607 (1991)
Ricci, V., Wennberg, B.: On the derivation of a linear Boltzmann equation from a periodic lattice gas. Stoch. Process. Appl. 111(2), 281–315 (2004)
Shah, N.A.: Limit distributions of expanding translates of certain orbits on homogeneous spaces. Indian Acad. Sci. Proc. Math. Sci. 106(2), 105–125 (1996)
Siegel, C.L.: A mean value theorem in geometry of numbers. Ann. Math. (2) 46, 340–347 (1945)
Veech, W.A.: Siegel measures. Ann. Math. (2) 148(3), 895–944 (1998)
Acknowledgments
We thank Alex Eskin, Alex Furman, Amos Nevo, and Andreas Strömbergsson for stimulating discussions, and MSRI for its hospitality during the programme “Geometric and Arithmetic Aspects of Homogeneous Dynamics.” The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013) / ERC Grant Agreement No. 291147.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Marklof, J., Vinogradov, I. Spherical averages in the space of marked lattices. Geom Dedicata 186, 75–102 (2017). https://doi.org/10.1007/s10711-016-0180-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10711-016-0180-2