Analytical theory of species abundance distributions of a random community model

Abstract

We review the history and recent progress of the analytical theories of a random community models. In particular, we focus on a global stability analysis of replicator equations with random interactions and species abundance distributions based on statistical mechanics.

Appendix

Informations on equilibrium states of dynamics of Eq. 20 at $t\rightarrow \infty$ is derived from the generating functional

$$\begin{aligned} \overline{Z[\varvec{\psi }]}&= \overline{\int D\varvec{x}\, \left( \prod _ip_0(x_i(0))\right) \exp \left( i\sum _{i=1}\int {\mathrm{d}}t\psi _i(t)x_i(t)\right) }\nonumber \\&\quad \times \overline{\prod _{i,t}\delta \left( \frac{\dot{x}_i(t)}{x_i(t)} - \sum _{j=1}a_{ij}x_j(t)+\bar{f}(t)-h(t)\right) } \end{aligned}$$

(25)

where $\overline{(\cdots )}$ is same as the random average in Eq. 9 over Gaussian distribution of $a_{ij}$ and a function $\psi _i(t)$ is another perturbation field introduced for further calculations such as $h(t)$ in Eq. 20. The function $\bar{f}(t)$ denotes the average fitness in Eq. 20. The function $p_0(x_i(0))$ denotes a distribution of an initial state of the population $x(0)$ of species $i$ (initial SAD). Important functions such as the correlation function $C(t,t')$ and the response function $G(t,t')$ are given by variation

$$\begin{aligned} C(t,t')=\frac{1}{N}\sum _{i=1}^N\overline{\left\langle x_i(t)x_i(t')\right\rangle } = \left. \frac{1}{N}\sum _{i=1}^N\frac{\delta ^2\overline{Z[\varvec{\psi }]}}{\delta i\psi _i(t)\delta i\psi _i(t')}\right| _{\varvec{\psi }=0} \end{aligned}$$

(26)

$$\begin{aligned} G(t,t')=\frac{1}{N}\sum _{i=1}^N\overline{\left\langle \frac{\delta x_i(t)}{\delta h(t')}\right\rangle } = \left. \frac{1}{N}\sum _{i=1}^N\frac{\delta ^2\overline{Z[\varvec{\psi }]}}{\delta h(t)\delta i\psi _i(t')}\right| _{\varvec{\psi }=0} \end{aligned}$$

(27)

where $\langle \cdots \rangle$ denotes an average over all trajectories of $x_i(t)$ (a path integral $\int D\varvec{x}$ in Eq. 25).

We do not enter into the detailed mathematics here, as they have been reported in depth in the literature (Opper and Diederich 1992; Galla 2006; Yoshino et al. 2008). After the random average of $Z[\varvec{\psi }]$ and the calculation of the path integral using the saddle point method, the system is found to be described by an effective single-species process with time delay (a multiplicative Gaussian stochastic process)

$$\begin{aligned} \frac{{\mathrm{d}}x(t)}{{\mathrm{d}}t} = x(t) \left( ux(t) - \gamma \int _0^t{\mathrm{d}}t' G(t,t') x(t') + \eta (t) - \bar{f}(t) + h(t) \right) \end{aligned}$$

(28)

This process is non-Markovian, and is subject to colored Gaussian noise $\eta (t)$, with temporal correlations given by

$$\begin{aligned} \left\langle \eta (t)\eta (t')\right\rangle =C(t,t'). \end{aligned}$$

(29)

Using this effective process, the correlation function and the response function are to be determined self-consistently as

$$\begin{aligned} C(t,t')=\left\langle x(t)x(t')\right\rangle _e,\quad G(t,t')=\left\langle \frac{\delta x(t)}{\delta h(t')}\right\rangle _e \end{aligned}$$

(30)

where $\langle \cdots \rangle _e$ denotes an average over trajectories of the effective stochastic process of Eq. 28.

The analysis proceeds by making a fixed point ansatz $x(t)=x, h(t)=h$ in the effective process, leading to

$$\begin{aligned} \forall \tau \, \lim _{t\rightarrow \infty } C(t+\tau ,t)=q,\qquad \lim _{t\rightarrow \infty }\bar{f}(t)=\bar{f}. \end{aligned}$$

(31)

Furthermore we assume time-translation invariance of the response

$$\begin{aligned} \lim _{t\rightarrow \infty }G(t+\tau ,t)=G(\tau ), \end{aligned}$$

(32)

finite integrated response and no long-term memory

$$\begin{aligned} \chi = \int _0^\infty {\mathrm{d}}\tau G(\tau ) <\infty ,\qquad \lim _{t\rightarrow \infty }G(t,t')=0. \end{aligned}$$

(33)

Within the fixed-point ansatz we also assume that each realization of the single-species noise $\{\eta (t)\}$ approaches a time-independent value asymptotically, which is then a Gaussian variable with zero mean and variance

$$\begin{aligned} \left\langle \eta ^2\right\rangle = q. \end{aligned}$$

(34)

Fixed points of Eq. 28 then fulfill the condition

$$\begin{aligned} x(ux -\gamma \chi x + \sqrt{q}z - \bar{f})=0 \end{aligned}$$

(35)

where $z\equiv \eta /\sqrt{q}$ is a standard Gaussian variable. The above algebraic equation has an "extinct" solution $x(z)=0$ for all realizations of the random variable $z$ and "non-extinct" solution

$$\begin{aligned} x(z)=\frac{\bar{f} - \sqrt{q}z}{u-\gamma \chi }\Theta \left[ \bar{f} - \sqrt{q}z\right] \, (\!{>}\!0), \end{aligned}$$

(36)

with the step function ($\Theta [x] =1\,\text{ for }\, x>0\,\text{ and }\, \Theta [x]=0\,\text{ for }\, x\le 0$). Whenever the non-extinct solution exists, the extinct solution is unstable, and finally the following self-consistent equations of the variables $\{q, \chi , \bar{f}\}$ ("order parameters") can then be derived for the two external parameters: productivity $u$ and the level of symmetry $\gamma$

$$\begin{aligned}&\left( u-\gamma \chi \right) =\sqrt{q}\int _{-\infty }^\Delta {\mathrm{D}}z (z+\Delta ) \end{aligned}$$

(37)

$$\begin{aligned}&\left( u-\gamma \chi \right) ^2 = \int _{-\infty }^\Delta {\mathrm{D}}z (z+\Delta )^2\end{aligned}$$

(38)

$$\begin{aligned}&\left( u-\gamma \chi \right) \chi =\int _{-\infty }^\Delta {\mathrm{D}}z\end{aligned}$$

(39)

$$\begin{aligned}&\Delta = \frac{\bar{f}}{\sqrt{q}} \end{aligned}$$

(40)

where ${\mathrm{D}}z\equiv({\mathrm{d}}z/\sqrt{2\pi })\exp (-z^2/2)$ denotes the standard Guassian measure. In the case of symmetric interactions ($\gamma =1$) the above equations are same as the result obtained by the different analysis for the symmetric random community model. The set of integral equations Eqs. 37–39 is, in general, not analytically solvable except for special values of parameters $u$ and $\gamma$ and is solved numerically, which is much easier than direct simulations of REs.

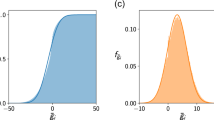
If we define the survival function $\alpha _{u,\gamma }(x)$ in the same way as $\alpha _u(x)$ in the symmetric random community model which is the probability that population of an arbitrary species takes a value larger than $x$, it is found to equal the probability that a standard Gaussian variable takes smaller value than $z(x)=\Delta -(u-\gamma \chi )x/\sqrt{q}$ given by Eq. 36 as

$$\begin{aligned} \alpha _{u,\gamma }(x)&= \frac{1}{\sqrt{2\pi }}\int _{-\infty }^{z(x)}{\mathrm{e}}^{-\frac{t'^2}{2}}{\mathrm{d}}t'\nonumber \\&= \frac{1}{2}+\frac{1}{\sqrt{2\pi }}\int _0^{z(x)}{\mathrm{e}}^{-\frac{t'^2}{2}}{\mathrm{d}}t'\nonumber \\&= \frac{1}{2}+\frac{1}{2}\text{ erf }(z(x)/\sqrt{2})\nonumber \\&= \frac{1}{2}\left[ 1+\text{ erf }\left( \frac{\Delta - \frac{u-\gamma \chi }{\sqrt{q}}x}{\sqrt{2}} \right) \right] \end{aligned}$$

(41)

and the diversity is given by

$$\begin{aligned} \alpha _{u,\gamma }(0)=\int _{-\infty }^\Delta {\mathrm{D}}z \end{aligned}$$

(42)

which is the same as $\alpha _u(0)$ of the symmetric random community model if $\gamma$ is set to $1$.

Table 1 Relations between the level of symmetry and the characteristics of the random community model

Fig. 1

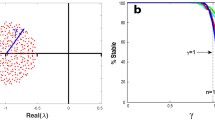
Phase diagram of the random community model. The horizontal axis denotes the level of symmetry $\gamma$ of the inter-species interactions and the vertical axis denotes the strength of the intraspecific competition $u$. A–C corresponds to the fully antisymmetric case (Chawanya and Tokita 2002), the stable–unstable transition point obtained by the linear stability analysis (May 1972) and the so-called spin glass transition point (Mezard et al. 1987), respectively