Introduction

For many years, a lot of effort has been put to find a way of quantitative prediction of the elasticity of polymer liquids from measurements of non-Newtonian viscosity during the shear flow. The elasticity of polymer melts and solutions in shear flows manifests itself through the existence of two non-zero normal stress differences, first of all of the primary normal stress difference. Though the shear viscosity and the first normal stress coefficient are different material functions, it does not mean that they are quite independent of each other. This is a result of the fact that both functions can be formally treated as different moments of the relaxation spectrum of a polymer liquid (Malkin 2006). Moreover, the appearance of non-zero normal stress differences is accompanied by some viscosity lowering with a rise of the shear intensity. It is also true in the case of highly elastic Boger fluids, which are generally treated as fluids with a constant (Newtonian) viscosity but really show a very weak pseudoplastic behavior (e.g. James 2009). On the other hand, purely Newtonian, low molecular liquids demonstrate no elastic properties. However, there exist also many non-polymeric liquid systems (e.g. different suspensions) with strong pseudoplasticity but negligible elasticity. For typical polymeric fluids, both features are well balanced that give rise to the looking for methods of elasticity determination based on the shape of viscosity or flow curves, which can be experimentally determined much easier than the normal stress differences.

At least several expressions making possible the calculation of the primary normal stress difference (normal stress coefficient) from the viscosity function were presented in the literature. They can be divided into two general groups. The first one contains integral models, while the second one can be referred to as differential models.

One of the oldest integral models was derived by Malkin (1971). It makes use of the above-mentioned fact that viscous and elastic properties of polymers result from the same relaxation time spectrum. This statement for relative small shear rates leads to the expression

$$ {N}_1\left(\dot{\gamma}\right)=\frac{4}{\pi }{\dot{\gamma}}^2{\displaystyle {\int}_0^{\infty}\frac{\eta \left(\dot{\gamma}\mathit{\hbox{'}}\right)}{{\dot{\gamma}}^2-\dot{\gamma}\;{\mathit{\hbox{'}}}^2}d}\dot{\gamma}\mathit{\hbox{'}} $$
(1)

where N 1 is the first normal stress difference, η is the viscosity and \( \dot{\gamma} \) is the shear rate.

The next expression of similar type was proposed by Abdel-Khalik et al. (1974). It is derived from the Goddard-Miller constitutive equation (Goddard and Miller 1966) with the use of Kramers-Kronig relations and has the form

$$ {N}_1\left(\dot{\gamma}\right)=\frac{4K}{\pi }{\dot{\gamma}}^2{\displaystyle {\int}_0^{\infty}\frac{\eta \left(\dot{\gamma}\right)-\eta \left(\dot{\gamma}^{\prime}\right)}{\dot{\gamma}{\prime}^2-{\dot{\gamma}}^2}d\dot{\gamma}^{\prime }} $$
(2)

where K is the empirical constant; K = 2 for solutions and K = 3 for melts.

The last well-known equation of integral type was derived by Gleissle (1980) from his two empirical “mirror relations” comparing the viscosity and elasticity in transient and steady shear flows. For this reason, it is sometimes referred to as the “third mirror relation”

$$ {N}_1\left(\dot{\gamma}\right)=2{\dot{\gamma}}^2{\displaystyle {\int}_{\dot{\gamma}/k}^{\infty }{\left(\dot{\gamma}\prime \right)}^{-1}\frac{\partial \eta \left(\dot{\gamma}^{\prime}\right)}{\partial \dot{\gamma}^{\prime }}d\dot{\gamma}^{\prime }} $$
(3)

where (2 < k < 3) is the empirical constant.

It should be noted that practical calculations with the use of integral models are not simple due to the specific structure of Eqs. (1-3). For this reason, such models are rather seldom applied for calculations in contrast to various differential models discussed below, which are much more simple.

The existing differential models represent the primary normal stress difference as a function of viscosity or its shear rate derivatives. They contain expressions resulting not only from the steady shear flow but also from the oscillatory shear flow.

The first expression of this type was derived by Wagner (1977), with the use of his own, well-known constitutive equation (Wagner 1976), and has the form

$$ {N}_1\left(\dot{\gamma}\right)=\frac{1}{m}{\dot{\gamma}}^2\frac{d\eta \left(\dot{\gamma}\right)}{d\left|\dot{\gamma}\right|} $$
(4)

where the constant m is connected to the Wagner damping function for a given polymer.

The next model proposed recently by Sharma and McKinley (2012) has a form

$$ {N}_1\left(\dot{\gamma}\right)=2\eta \dot{\gamma}{\left\{1-{\left[\frac{\eta_c}{\eta}\right]}^2\right\}}^{0,5}{\left[\frac{\eta_c}{\eta}\right]}^{-1,4} $$
(5)

It is based on three empirical rules connecting the material functions in steady and oscillatory shear flows of polymer liquids, i.e.

the Laun rule (Laun 1986)

$$ {N}_1\left(\dot{\gamma}\right)\mathbf{\Big|}{}_{\omega =\dot{\gamma}}=2G^{\prime}\left(\omega \right){\left\{1+{\left[\frac{G\prime \left(\omega \right)}{G{\prime\prime} \left(\omega \right)}\right]}^2\right\}}^{0,7} $$
(6)

where G '(ω) and G ''(ω) are the storage and loss moduli as functions of the frequency ω

and the two Cox-Merz rules (Cox and Merz 1958)

$$ \left|{\eta}^{*}\left(\omega \right)\right|\kern0.5em =\eta \left(\overset{\cdotp }{\gamma}\right)\Big|{}_{\omega =\overset{\cdotp }{\gamma }} $$
(7a)
$$ \left|{\eta}^{\prime}\left(\omega \right)\right|\kern0.5em ={\eta}_{\mathrm{c}}\left(\dot{\gamma}\right)=\frac{d\tau }{d\dot{\gamma}}\left|{}_{\omega =\dot{\gamma}}\right. $$
(7b)

where \( {\eta}_{\mathrm{c}}\left(\dot{\gamma}\right) \) is the consistency (tangent viscosity), \( \eta \left(\dot{\gamma}\right) \) is the apparent (secant) viscosity, η ∗(ω) and η ′(ω) are the complex viscosity and the real part of complex viscosity and τ is the shear stress.

Equation (7a) is widely known and applied, while Eq. (7b) is somewhat forgotten.

Another empirical formula for calculation of the first normal stress difference from the data of oscillatory measurements was also proposed by Al-Hadithi et al. (1992).

There are also several works which compare various formulas for prediction of the first normal stress difference from viscosity measurements (Stastna and De Kee 1982) or propose new methods for calculation of the melt elasticity from viscometric data based on the Wagner model (Youngwook and Yongsok 2012). The interesting general method for calculation of the primary normal stress coefficient with the use of the theory of linear operators was also presented (Friedrich and Heymann 1988).

The aim of this paper is to present a new model for calculation of the primary normal stress difference from a generalized viscosity function. Moreover, the proposed model along with other differential models discussed above is further transformed into the shear stress-dependent and simultaneously temperature-invariant form. It enables a simple determination of the elasticity of polymer liquids from their flow curve.

Calculation of the first normal stress difference from generalized viscosity curve

For further considerations, it is convenient to introduce the definition of the generalized viscosity function of the power-law type in the following form:

$$ {\eta}^v=f\left({\dot{\gamma}}^v\right) $$
(8)

where ν is any real number, and the case ν = 1 corresponds to the ordinary viscosity curve.

The analysis of experimental results on the shear viscosity and the first normal stress difference for various polymer liquids leads to the conclusion that these results can be very well correlated by means of the following empirical equation:

$$ {N}_1\left(\dot{\gamma}\right)=12{\dot{\gamma}}^2\sqrt{-\frac{d\left({\eta}^2\right)}{d\left({\dot{\gamma}}^2\right)}}\kern0.5em {\left[2+\frac{d\mathit{\ln}\left({\eta}^2\right)}{d\mathit{\ln}\left({\dot{\gamma}}^2\right)}\right]}^{-4} $$
(9)

It is based on the generalized viscosity function corresponding to ν = 2 in Eq. (8) and the results of dimensional analysis presented later. Such form reflects the theoretical fact that the viscosity as an even function should be dependent only on even powers of the shear rate. The calculated values of N 1 are very sensitive to the changes in values of corresponding derivatives of the viscosity function. Hence, the practical use of Eq. (9) for calculations requires, as a rule, the smoothing of experimental data by means of an adequate viscosity equation in generalized form and non-linear regression. In this case, calculations were performed using the own four-parameter viscosity equation discussed in details elsewhere (Steller 2013; Steller 2015)

$$ \frac{\eta }{\eta_0}={\left[1+\beta {\left(\lambda \dot{\gamma}\right)}^2+{\left(\lambda \dot{\gamma}\right)}^4\right]}^{\frac{n-1}{4}} $$
(10)

where η 0, λ, β and n ≤ 1 are positive material constants.

Equation (10) can be treated as an extension of the well-known three-parameter Carreau model (Carreau 1972) corresponding to β = 2. It has the properties similar to another four-parameter extension of the Carreau model, i.e. Carreau-Yasuda Eq. (11) (Yasuda et al. 1981), which, in some cases, was also used for comparison.

$$ \frac{\eta }{\eta_0}={\left[1+{\left(\lambda \dot{\gamma}\right)}^{\alpha}\right]}^{\frac{n-1}{\alpha }} $$
(11)

where η 0, λ, α and n ≤ 1 are positive material constants (for α = 2, the Carreau equation is obtained).

Both equations describe very well viscosity curves of polymers with a wide transition region between Newtonian and power-law behavior. However, Eq. (10) depends only on even powers of the shear rate in contrast to Eq. (11), which contains the fractional powers of the shear rate. For this reason, Eq. (10) seems to be theoretically more proper.

The generalized form of Eq. (10) for any value of ν can be expressed as

$$ {\eta}^v={\eta}_0^v{\left[1+\beta {\lambda}^2{x}^{\frac{2}{v}}+{\lambda}^4{x}^{\frac{4}{v}}\right]}^{\frac{\left(n-1\right)v}{4}} $$
(12)

where \( x={\dot{\gamma}}^{\nu } \) and ν = 2 in this case.

Equation (12) makes it possible to calculate the derivatives in expression (9) for known values of the four material constants, which, in turn, are estimated from experimental data \( {\eta}^2=f\left({\dot{\gamma}}^2\right) \) by means of a non-linear regression. The results are not stable in the sense that the estimated parameters depend strongly on how function (12) is expressed, e.g. as given by formula (12) or as (η/η 0)ν or as ν ln (η/η 0) This is also true for the generalized form of the Carreau-Yasuda equation. It seems that the logarithmic form is generally most appropriate, as shown below. Moreover, the results depend also on the viscosity model used for calculations.

The calculation results will be presented, taking as an example the numerical data on shear viscosity and the first normal stress difference measurements for 11.4 % polyisobutylene solution in 2,6,10,14-tetramethylpentadecane (Pristan) at 0 °C (Schultheisz and Leigh 2002).

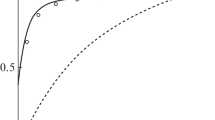
The estimated parameters of the generalized viscosity function expressed in form (12) or as (η/η 0)2 are almost the same and equal to η 0 = 382.2 Pa·s, λ = 3.168 s, β = 8.64 and n = 0.490. The logarithmic form 2 ln (η/η 0) leads to quite different estimates: η 0 = 379.9 Pa·s, λ = 1.064 s, β = 25.75 and n = 0.290. It can be easily checked that the first set of parameters gives the theoretical function \( {\eta}^2=f\left({\dot{\gamma}}^2\right) \), which overestimates strongly the experimental values in the region of high \( {\dot{\gamma}}^2>100 \); e.g. for \( {\dot{\gamma}}^2=10,000 \), the predicted value of η 2 = 410 instead of 82 resulting from the measurement. The second set of parameters obtained from the logarithmic form provides a very good fit of data shown in Fig. 1. The parameters η 0 = 411.3 Pa·s, λ = 0.744 s, α = 0704 and n = 0.136 estimated for the Carreau-Yasuda equation in the logarithmic form give also a very good data fit. The corresponding curve coincides practically with that in Fig. 1, and for this reason, it was not shown. The relative viscosity differences resulting from both models do not exceed 3 %. Similarly, the estimates η 0 = 388.6 Pa·s, λ = 2766 s, α = 1116 and n = 0.452 obtained for the other forms mentioned earlier lead to similar discrepancies as in the case of Eq. (12); e.g. for \( {\dot{\gamma}}^2=10,000 \), the predicted η2 = 320 instead of 82. It should be also noted that such behavior is observed for the least-squares method as the estimation criterion.

Fig. 1
figure 1

Comparison of experimental data (full squares) with predictions (solid line) of generalized viscosity function (12) for ν = 2

Full size image

Figure 2 presents the experimental data for the first normal stress difference compared with values predicted by Eq. (9) with the use of generalized expressions (10) and (11) for calculations of both derivatives. It can be seen that a general agreement of measured and calculated data is quite well in both cases. However, small quantitative differences in the course of the curves \( {\eta}^2=f\left({\dot{\gamma}}^2\right) \) resulting from Eqs. (10) and (11) have a visible effect on the course of corresponding normal stress curves \( {N}_1=g\left(\dot{\gamma}\right) \), which are very sensitive to the change of the viscous characteristics. The relative differences in N 1 calculated from both models may exceed 30 %; i.e. they are ca. ten times larger than the corresponding viscosity differences. A similar behavior testifying to the low stability of normal stress calculations based on the viscosity curve was also observed for other systems. It should be also noted that both the viscosity and its square are quantities calculated from the primary measurements data, i.e. the shear stress and the shear rate. The primary measurement errors are, as a rule, increased during mathematical operations such as division or exponentiation. This can be treated as an additional source of uncertainty affecting negatively the stability of normal stress calculations based on the viscosity curve. For this reason, a more efficient method for the normal stress calculations based on the flow curve was developed and is discussed below.

Fig. 2
figure 2

Comparison of experimental values (full triangles) of the first normal stress difference with theoretical values calculated from Eq. (9) with the use of generalized Eq. (10) (solid line) and generalized Eq. (11) (dotted line)

Full size image

Calculation of the first normal stress difference from the flow curve

Very interesting results are obtained if viscosity-dependent expressions (4), (5) and (9) for calculations of the first normal stress difference are transformed into the shear stress-dependent forms. It can be easily done using the general equation of the flow curve

$$ \tau =\eta \left(\dot{\gamma}\right)\dot{\gamma} $$
(13)

Denoting for convenience the local slope of the flow curve as

$$ n=\frac{dln\tau }{dln\dot{\gamma}} $$
(14)

one obtains

  • Wagner Eq. (4)

$$ {N}_1\left(\dot{\gamma}\right)=\frac{1}{m}\left|\tau \right|\left(1-n\right) $$
(15)

  • Sharma-McKinley Eq. (5)

$$ {N}_1\left(\dot{\gamma}\right)=2\left|\tau \right|\sqrt{1-{n}^2}\kern0.5em {n}^{-1.4} $$
(16)

  • Own Eq. (9)

$$ {N}_1\left(\dot{\gamma}\right)=12\left|\tau \right|\sqrt{1-n}\kern0.5em {\left(1+n\right)}^{-4} $$
(17)

It can be easily seen from expressions (15–17) that the ratio of the normal and shear stresses \( \left(\frac{N_1}{\tau}\right) \) sometimes referred to as the Weissenberg number is a unique function of the local slope (n) of the flow curve. Moreover, the ratio is most probably independent of temperature.

To check this theoretical result, the local slopes and the corresponding Weissenberg numbers were determined from experimental data for eight systems of linear polymers, i.e. polyisobutylene (PIB) solution at 0, 25 and 50 °C (Schultheisz and Leigh 2002); polydimethylsiloxane (PDMS) at 0, 25 and 50 °C (Schultheisz et al. 2003); and high-density polyethylene (HDPE) and polypropylene (PP) melts at 200 °C. The data for both melts were recalculated from quantitative material functions resulting from an integral constitutive equation, which was presented much earlier (Steller 1985).

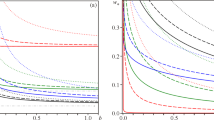
The obtained data are shown in Fig. 3, where, for convenience as an independent variable, the values of 1 − n instead of n were applied. It is clearly seen that all experimental points for various polymers and temperatures create a common master curve (despite small data scattering). It is an excellent confirmation of qualitative predictions resulting from Eqs. (15–17) independent of their adequacy.

Fig. 3
figure 3

Temperature-invariant representation of stress ratio for various linear polymers

Full size image

The temperature invariance of the stress ratio results also indirectly from other studies. In many cases, the correlation of power-law type between normal and shear stresses was observed, e.g. (Carreau et al. 1997)

$$ {N}_1=K{\left|\tau \right|}^m $$
(18)

It was found (Jomha and Reynolds 1993) that for polyethylene melt and water solution of polyacrylamide, formula (18), which can be also expressed as the stress ratio, is independent of temperature. A similar behavior was also observed in various EPDM compounds (Markovic et al. 2000).

It should be also noted that the determination of the slope of the flow curve given by Eq. (14) from the experimental data can be done as a rule without using any special function as in the case of the viscosity curve. This is due to the fact that the flow curve in the logarithmic form \( \ln \tau =f\left( \ln \dot{\gamma}\right) \) can be easily described by means of polynomial regression in contrast to the viscosity curve \( \ln \eta =g\left( \ln \dot{\gamma}\right) \), which tends to have a constant value lnη 0, if \( \ln \dot{\gamma} \) tends to −∞. To describe adequately such an asymptotic behavior, a suitable viscosity model must be used.

Figure 4 presents the comparison of theoretical values of the stress ratio provided by Eqs. (15–17) with the experimental data from Fig. 3. In Wagner Eq. (15), the mean value of m = 1/3 was assumed according to the data quoted in Wagner (1977)). It can be seen that the Wagner formula works quite well for n > 0.5, while Sharma-McKinley Eq. (16) strongly overestimates the experimental values of stress ratio. Equation (17) provides an excellent fit of data. The correlation quality is better seen on a linear graph obtained from Fig. 4 by substituting for 1 − n the values of function (17) on the x-axis. It is shown in Fig. 5.

Fig. 4
figure 4

Comparison between experimental stress ratio values and predictions of Eqs. (15, Wagner), (16, Sharma) and (17, the author)

Full size image
Fig. 5
figure 5

Correlation between experimental and theoretical stress ratio values calculated from Eq. (17, 26, 28, 29)

Full size image

Figure 6 presents for comparison the data for PIB solution from Fig. 2 described by means of Eq. (17). In this case, a smooth, monotonic curve is obtained, which fits to the experimental data very well.

Fig. 6
figure 6

Comparison of experimental values (full triangles) of the first normal stress difference with theoretical values (solid line) calculated from Eq. (17)

Full size image

For further generalization or improvement of the above results, dimensional analysis was performed. It has the goal to show that, in the general case, the stress ratio can be represented as a unique function of the local slope of the viscosity or flow curve. It makes also possible to find the admissible forms of (simple) functions which may define the first normal stress coefficient Ψ 1 expressed in Pa·s2 or the first normal stress difference N 1 expressed in pascals.

There are, in principle, two linearly independent quantities of the dimension of Pa·s2 connecting the viscosity η and the shear rate \( \dot{\gamma} \). The first one has the form of a quotient

$$ {f}_1=\frac{\eta }{\dot{\gamma}} $$
(19)

while the second one can be represented by the following expression resulting from the definition of generalized viscosity function (8):

$$ {f}_2={\left(-\frac{d\left({\eta}^{\mu}\right)}{d\left({\dot{\gamma}}^{\mu}\right)}\right)}^{\frac{1}{\mu }} $$
(20)

It contains the first derivative of generalized power-law-type viscosity function (8). From various linear combinations of Eqs. (19) and (20) raised to the same power, a new quantity can be created and then transformed into an expression with the dimension of Pa·s2 corresponding to \( {\psi}_1\left(\dot{\gamma}\right) \) or to \( {N}_1\left(\dot{\gamma}\right) \) after multiplying by \( {\dot{\gamma}}^2 \). In the most simple case, one obtains the formula

$$ \left|A\right){\scriptscriptstyle \left(\frac{\eta }{\dot{\gamma}}\right)}{\left({}^{\mu }+B{\scriptscriptstyle \frac{d\left({\eta}^{\mu}\right)}{d\left({\dot{\gamma}}^{\mu}\right)}}\right|}^{\frac{1}{\mu }}={\scriptscriptstyle \frac{\eta }{\dot{\left|\gamma \right|}}}{\left|A+B{\scriptscriptstyle \frac{dln\eta }{dln\dot{\gamma}}}\right|}^{\frac{1}{\mu }} $$
(21)

which has the dimension of Pa·s2 (A and B are dimensionless constants).

In Eq. (21), the following property of generalized viscosity function (8) was used:

$$ \frac{dln{\eta}^{\mu }}{dln{\dot{\gamma}}^{\mu }}=\frac{dln\eta }{dln\dot{\gamma}} $$
(22)

Expression (21) with different values of A, B and μ makes it possible to create various products and/or linear combinations with the dimension of Pa·s2 or pascals. Therefore, the general expression for the primary normal stress difference resulting from the dimensional analysis and expressed in terms of the viscosity curve can be formulated in the following way:

$$ {N}_1=\eta \left|\dot{\gamma}\right|{\displaystyle {\sum}_j{C}_j{\displaystyle {\prod}_i{\left|{A}_{ij}+{B}_{ij}\frac{dln\eta }{dln\dot{\gamma}}\right|}^{\nu_{i\;j}}}} $$
(23)

Using the equation of the flow curve (Eq. (13)), expression (23) can be easily transformed into the shear stress-dependent form

$$ {N}_1=\left|\tau \right|{\displaystyle {\sum}_j{C}_j{\displaystyle {\prod}_i{\left|{A}_{ij}+{B}_{ij}\left(n-1\right)\right|}^{\nu_{i\;j}}}} $$
(24)

where the local slope of the flow curve given by formula (14) varies in the range 0 < n ≤ 1.

In the Newtonian flow region, i.e. for n = 1, Eq. (24) must fulfil the condition N 1 = 0, which determines the choice of constants A, B and C. Assuming for simplicity j = 1, A 11 = 0, B 11 = 1 and ν 11 > 0, Eq. (24) can be rearranged to the form satisfying the above condition

$$ \frac{N_1}{\left|\tau \right|}={C}_1{\left(1-n\right)}^{\nu_{11}}{\displaystyle {\prod}_{i>1}{\left|{A}_{i1}+{B}_{i1}\left(n-1\right)\right|}^{\nu_{i1}}} $$
(25)

It can be easily seen that Eqs. (15–17) have exactly the form of expression (25). In Eq. (16), the identity 1 − n 2 = (1 − n)(1 + n) should only be taken into account.

Equations of type (24) comprising the sums of two or more terms may have a much more complicated structure, which also fulfil the condition N 1 = 0 for n = 1. Some examples of such functions describing correctly the stress ratio will be given below (Eqs. (28) and (29)).

Based on the results of dimensional analysis and, in particular, on the use of simple functions of power-law type suggested by formula (25), the equations of Wagner and Sharma-McKinley can be modified to provide a very good agreement of predicted and measured values of the stress ratio. The characteristic terms in Wagner and Sharma equations are (1 − n) and (1 − n 2)0.5, respectively. Using the trial-and-error method supported by the non-linear regression, it was found that the simplest extension of the Wagner equation corresponding to formula (25), which quantitatively describes the data from Fig. 3, has the form

$$ \frac{N_1}{\left|\tau \right|}=14\left(1-n\right){\left(1+6n\right)}^{-1} $$
(26)

The approximation exactness of Eq. (26) is shown in Fig. 7 (similar to Fig. 5).

Fig. 7
figure 7

Correlation between experimental and theoretical stress ratio values calculated from Eq. (17, 26, 28, 29)

Full size image

It should be noted that the term 14(1 + 6n)−1 in Eq. (26) can formally be treated as the local value of the inverse of the damping constant m in Wagner formula (15). Assuming n = 0.5 as the mean interval value, one obtains 3.5 as the inverse of the mean m value. The graph for the Wagner equation in Fig. 4 was constructed, assuming 1 / m = 3 for n > 0.5.

In the case of the Sharma-McKinley equation, the best fit to experimental data provides the following modification:

$$ \frac{N_1}{\left|\tau \right|}=12\sqrt{1-{n}^2}{\left(1+n\right)}^{-4.5} $$
(27)

It is the same equation as Eq. (17) proposed in this work but written in another form.

It should be also noted that all numbers (except 1) appearing in Eqs. (26) and (17) or (27) were rounded to provide the simplest forms of these equations. However, the rounding errors are less than 2–3 % and have no practical meaning.

There are also possible other more complicated formulas, which very well describe the data from Fig. 3 and are generally consistent with the results of dimensional analysis. Two examples of such expressions are given below:

$$ \frac{N_1}{\left|\tau \right|}=11\left(1-{n}^{0.2}\right){n}^{-0.3} $$
(28)

The corresponding chart is shown in Fig. 8.

$$ \frac{N_1}{\left|\tau \right|}=\frac{5}{3}\mathit{\ln}{\left(\frac{n^2-n+{\scriptscriptstyle \frac{5}{3}}}{{\scriptscriptstyle \frac{5}{3}}n}\right)}^2 $$
(29)
Fig. 8
figure 8

Correlation between experimental and theoretical stress ratio values calculated from Eq. (17, 26, 28, 29)

Full size image

It is interesting to note that logarithmic expression (29) has only one constant (5/3) appearing in three different places. The plot corresponding to function (29) is presented in Fig. 9.

Fig. 9
figure 9

Correlation between experimental and theoretical stress ratio values calculated from Eq. (17, 26, 28, 29)

Full size image

It should be also noted that Eqs. (26) and (17) or (27) predict the finite stress ratio values for the limiting case n = 0. They are quite similar and equal to 14 and 12, respectively. On the other hand, functions (28) and (29) increase unlimitedly if n tends to zero. The true behavior of the stress ratio in such case is not quite clear from the theoretical point of view. It seems that the assumption of the limited value of the stress ratio is more proper, considering that the damping constant in Wagner Eq. (15) should have, most probably, a non-zero, positive value (m > 0). In such case, Eqs. (28) and (29) must be treated as two adequate regression formulas with no special theoretical meaning.

It is also noteworthy that all equations proposed for determination of the first normal stress difference from the viscosity curve or the flow curve are also valid for the oscillatory shear flow, if the Cox-Merz rule given by expression (7a) holds. In the oscillatory shear flow, the following relation is always valid:

$$ \left|{G}^{*}\left(\omega \right)\right|=\left|{\eta}^{*}\left(\omega \right)\right|\omega $$
(30)

It can be easily seen, if Eq. (7a) is fulfilled than Eq. (30) and the equation of the flow curve (Eq. (13)) become equivalent, i.e. \( \eta \left(\dot{\gamma}\right) \) may be replaced by |η ∗(ω)| and \( \tau \left(\dot{\gamma}\right) \) by |G ∗(ω)|.

Conclusions

A comprehensive analysis of existing and newly proposed semiempirical or empirical expressions for calculation of the first normal stress difference from the data of viscosity measurements has been performed. It was shown that most useful results can be obtained by representing the ratio of normal and shear stresses as a function of the local slope of the flow curve. Such representation is unique and simultaneously temperature invariant. The proposed expressions describe very well the experimental data only for a limited number of 8 of various linear polymers in the form of melts and solutions at different temperatures, which were used as examples in this work. For this reason, a further experimental verification of obtained results is necessary for a larger number of polymer systems. Such verification should comprise not only linear polymers but also branched polymers and polymers with a much more complicated molecular structure, which differ in the average molecular weight and molecular weight distribution. It makes possible to ascertain if the proposed expressions are generally valid or are valid only for some groups of polymer melts or solutions.