Abstract
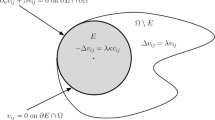
This paper focuses on the study of a linear eigenvalue problem with indefinite weight and Robin type boundary conditions. We investigate the minimization of the positive principal eigenvalue under the constraint that the absolute value of the weight is bounded and the total weight is a fixed negative constant. Biologically, this minimization problem is motivated by the question of determining the optimal spatial arrangement of favorable and unfavorable regions for a species to survive. For rectangular domains with Neumann boundary condition, it is known that there exists a threshold value such that if the total weight is below this threshold value then the optimal favorable region is like a section of a disk at one of the four corners; otherwise, the optimal favorable region is a strip attached to the shorter side of the rectangle. Here, we investigate the same problem with mixed Robin-Neumann type boundary conditions and study how this boundary condition affects the optimal spatial arrangement.
Similar content being viewed by others
References
Afrouzi, G.A.: Boundedness and monotonicity of principal eigenvalues for boundary value problems with indefinite weight functions. Int. J. Math. Math. Sci. 30(1), 25–29 (2002)
Afrouzi, G.A., Brown, K.J.: On principal eigenvalues for boundary value problems with indefinite weight and Robin boundary conditions. Proc. Am. Math. Soc. 127(1), 125–130 (1999)
Arnoldi, W.E.: The principle of minimized iteration in the solution of the matrix eigenvalue problem. Q. Appl. Math. 9, 17–29 (1951)
Belgacem, F.: Elliptic Boundary Value Problems with Indefinite Weights: Variational Formulations of the Principal Eigenvalue and Applications. Pitman Research Notes in Mathematics, vol. 368. Longman, Harlow (1997)
Bôcher, M.: The smallest characteristic numbers in a certain exceptional case. Bull. Am. Math. Soc. 21(1), 6–9 (1914)
Cantrell, R.S., Cosner, C.: Diffusive logistic equations with indefinite weights: population models in disrupted environments. Proc. R. Soc. Edinb. A 112(3–4), 293–318 (1989)
Cantrell, R.S., Cosner, C.: Diffusive logistic equations with indefinite weights: population models in disrupted environments, II. SIAM J. Math. Anal. 22(4), 1043–1064 (1991)
Cantrell, R.S., Cosner, C.: The effects of spatial heterogeneity in population dynamics. J. Math. Biol. 29(4), 315–338 (1991)
Cantrell, R.S., Cosner, C.: Spatial Ecology via Reaction-Diffusion Equations. Wiley Series in Mathematical and Computational Biology. Wiley, Chichester (2003)
Conca, C., Mahadevan, R., Sanz, L.: Shape derivative for a two-phase eigenvalue problem and optimal configurations in a ball. In: CANUM 2008, ESAIM Proc., vol. 27, pp. 311–321. EDP Sci., Les Ulis (2009)
Cox, S.: The two phase drum with the deepest bass note. Jpn. J. Ind. Appl. Math. 8, 345–355 (1991)
Cox, S., McLaughlin, J.: Extremal eigenvalue problems for composite membranes i and ii. Appl. Math. Optim. 22, 153–167 (1990)
Fleming, W.H.: A selection-migration model in population genetics. J. Math. Biol. 2(3), 219–233 (1975)
Grisvard, P.: Elliptic Problems in Nonsmooth Domains. Monographs and Studies in Mathematics, vol. 24. Pitman, Boston (1985)
He, L., Kao, C.-Y., Osher, S.: Incorporating topological derivatives into shape derivatives based level set methods. J. Comput. Phys. 225, 891–909 (2007)
Hess, P., Kato, T.: On some linear and nonlinear eigenvalue problems with an indefinite weight function. Commun. Partial Differ. Equ. 5(10), 999–1030 (1980)
Kao, C.Y., Su, S.: An efficient rearrangement algorithm for shape optimization on eigenvalue problems. In: IMA Workshop on Numerical Solutions of Partial Differential Equations: Fast Solution Techniques (2010)
Kao, C.-Y., Lou, Y., Yanagida, E.: Principal eigenvalue for an elliptic problem with indefinite weight on cylindrical domains. Math. Biosci. Eng. 5(2), 315–335 (2008)
Krein, M.G.: On certain problems on the maximum and minimum of characteristic values and on the Lyapunov zones of stability. Transl. Am. Math. Soc. 1(2), 163–187 (1955)
Lou, Y., Yanagida, E.: Minimization of the principal eigenvalue for an elliptic boundary value problem with indefinite weight, and applications to population dynamics. Jpn. J. Ind. Appl. Math. 23(3), 275–292 (2006)
Osher, J., Santosa, F.: Level set methods for optimization problems involving geometry and constraints i. Frequencies of a two-density inhomogeneous drum. J. Comput. Phys. 171, 272–288 (2001)
Saut, J.-C., Scheurer, B.: Remarks on a non-linear equation arising in population genetics. Commun. Partial Differ. Equ. 3(10), 907–931 (1978)
Skellam, J.G.: Random dispersal in theoretical populations. Biometrika 38, 196–218 (1951)
Sokołowski, J., Żochowski, A.: On the topological derivative in shape optimization. SIAM J. Control Optim. 37(4), 1251–1272 (1999)
Sokołowski, J., Zolésio, J.-P.: Introduction to Shape Optimization. Springer Series in Computational Mathematics, vol. 16. Springer, Berlin (1992). Shape sensitivity analysis
Su, S.: Numerical approaches on shape optimization of elliptic eigenvalue problems and shape study of human brains. Ph.D. thesis, The Ohio State University (2010)
Wayne, A.: Inequalities and inversions of order. Scr. Math. 12(2), 164–169 (1946)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hintermüller, M., Kao, CY. & Laurain, A. Principal Eigenvalue Minimization for an Elliptic Problem with Indefinite Weight and Robin Boundary Conditions. Appl Math Optim 65, 111–146 (2012). https://doi.org/10.1007/s00245-011-9153-x
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00245-011-9153-x