Modeling the Effect of Helical Fiber Structure on Wood Fiber Composite Elastic Properties

Abstract

The effect of the helical wood fiber structure on in-plane composite properties has been analyzed. The used analytical concentric cylinder model is valid for an arbitrary number of phases with monoclinic material properties in a global coordinate system. The wood fiber was modeled as a three concentric cylinder assembly with lumen in the middle followed by the S3, S2 and S1 layers. Due to its helical structure the fiber tends to rotate upon loading in axial direction. In most studies on the mechanical behavior of wood fiber composites this extension-twist coupling is overlooked since it is assumed that the fiber will be restricted from rotation within the composite. Therefore, two extreme cases, first modeling fiber then modeling composite were examined: (i) free rotation and (ii) no rotation of the cylinder assembly. It was found that longitudinal fiber modulus depending on the microfibril angle in S2 layer is very sensitive with respect to restrictions for fiber rotation. In-plane Poisson’s ratio was also shown to be greatly influenced. The results were compared to a model representing the fiber by its cell wall and using classical laminate theory to model the fiber. It was found that longitudinal fiber modulus correlates quite well with results obtained with the concentric cylinder model, whereas Poisson’s ratio gave unsatisfactory matching. Finally using typical thermoset resin properties the longitudinal modulus and Poisson’s ratio of an aligned softwood fiber composite with varying fiber content were calculated for various microfibril angles in the S2 layer.

Appendices

Appendix A

Stiffness transformation equations

The cell wall layer in the symmetry axes (L,T,r) is an unidirectional composite described as an orthotropic material with the stiffness matrix

$$ \left[ Q \right] = \left[ {\begin{array}{*{20}{c}} {{Q_{11}}} \hfill & {{Q_{12}}} \hfill & {{Q_{13}}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {{Q_{12}}} \hfill & {{Q_{22}}} \hfill & {{Q_{23}}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {{Q_{13}}} \hfill & {{Q_{23}}} \hfill & {{Q_{33}}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {{Q_{44}}} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {{Q_{55}}} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {{Q_{66}}} \hfill \\ \end{array} } \right] $$

(A1)

The stiffness matrix of this material in the global (z, φ, r)-system is given by (1). The stress components in the global system can be expressed through stresses in the local (L,T,r)-system using the well known tensor transformation expressions with rotation around the r-axis

$$ {\left[ \sigma \right]_{z,\varphi, r}} = {\left[ \alpha \right]^T}{\left[ \sigma \right]_{L,T,r}}\left[ \alpha \right] $$

(A2)

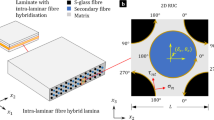
${\left[ \sigma \right]_{z,\varphi, r}}$ and ${\left[ \sigma \right]_{L,T,r}}$ is the stress component matrix in the global and local coordinates respectively, $\left[ \alpha \right]$ is the matrix of orientation cosines with elements defined as ${\alpha_{ik}} = \cos \left( {x_i^\prime, {x_k}} \right)$ for i,k = 1,2,3, where $x_i^\prime$is the coordinate axis in the local system and ${x_k}$is the axis in the global system. It can be shown that using notation $m = \cos \theta$, $n = \sin \theta$, see Fig. 1, we have the following expression

$$ \left[ \alpha \right] = \left[ {\begin{array}{*{20}{c}} m \hfill & n \hfill & 0 \hfill \\ { - n} \hfill & m \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right] $$

(A3)

Using (A3) in (A2) we obtain the following transformation matrix in vector form

$$ \left\{ {\begin{array}{*{20}{c}} {{\sigma_z}} \hfill \\ {{\sigma_\varphi }} \hfill \\ {{\sigma_r}} \hfill \\ {{\sigma_{\varphi r}}} \hfill \\ {{\sigma_{zr}}} \hfill \\ {{\sigma_{z\varphi }}} \hfill \\ \end{array} } \right\} = {\left[ {{T_{3D}}} \right]^{ - 1}}\left\{ {\begin{array}{*{20}{c}} {{\sigma_L}} \hfill \\ {{\sigma_T}} \hfill \\ {{\sigma_r}} \hfill \\ {{\sigma_{Tr}}} \hfill \\ {{\sigma_{Lr}}} \hfill \\ {{\sigma_{LT}}} \hfill \\ \end{array} } \right\}\;\;{\text{where}}\;\;{\left[ {{T_{3D}}} \right]^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {m^2} \hfill & {n^2} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - 2mn} \hfill \\ {n^2} \hfill & {m^2} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {2mn} \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & m \hfill & n \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & { - n} \hfill & m \hfill & 0 \hfill \\ {mn} \hfill & { - mn} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {{m^2} - {n^2}} \hfill \\ \end{array} } \right] $$

(A4)

Stiffness transformation expressions relating material stiffness matrix in the global (z, φ, r)-system with the stiffness in the local (L,T,r)-system can be obtained using a formal chain of rearrangements

$$ {\left\{ \sigma \right\}_{z,\varphi, r}} = {\left[ {{T_{3D}}} \right]^{ - 1}}{\left\{ \sigma \right\}_{L,T,r}} = {\left[ {{T_{3D}}} \right]^{ - 1}}\left[ Q \right]{\left\{ \varepsilon \right\}_{L,T,r}} = {\left[ {{T_{3D}}} \right]^{ - 1}}\left[ Q \right]{\left( {{{\left[ {{T_{3D}}} \right]}^{ - 1}}} \right)^T}{\left\{ \varepsilon \right\}_{z,\varphi, r}} $$

(A5)

The strain transformation in the last step in (A5) is slightly different because we are transforming engineering and not tensorial strains. Since (A5) establishes a relationship between stresses and strains in the global system, the matrix product linking them is the stiffness matrix of the material in these coordinates

$$ \left[ {\bar Q} \right] = {\left[ {{T_{3D}}} \right]^{ - 1}}\left[ Q \right]{\left( {{{\left[ {{T_{3D}}} \right]}^{ - 1}}} \right)^T} $$

(A6)

Appendix B

Strain –displacement relationships and stress equilibrium equations

The relationships between strain and displacement components in a cylindrical system of coordinates are

$$ {\varepsilon_z} = \frac{{\partial w}}{{\partial z}};{\varepsilon_r} = \frac{{\partial u}}{{\partial r}};{\varepsilon_\varphi } = \frac{u}{r} + \frac{1}{r}\frac{{\partial v}}{{\partial \varphi }};{\gamma_{\varphi r}} = \frac{{\partial v}}{{\partial r}} - \frac{v}{r} + \frac{1}{r}\frac{{\partial u}}{{\partial \varphi }};{\gamma_{zr}} = \frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial r}};{\gamma_{z\varphi }} = \frac{{\partial v}}{{\partial z}} + \frac{1}{r}\frac{{\partial w}}{{\partial \varphi }} $$

(B1)

In the following we consider loading cases where stress and strain components are z and φ independent, ε_z = ε₀ and the tangential tractions on the internal boundary r = r ₀ and also on the external boundary r = r _N of the sub-cylinder assembly are zero. The expressions for displacements and strains become

$$ w = {\varepsilon_0}z;\;\;u = {u_0}(r);\;\;v = {D_1}rz + {D_2}r $$

(B2)

$$ {\varepsilon_r} = \frac{{d{u_0}}}{dr};\;\;{\varepsilon_\varphi } = \frac{{{u_0}(r)}}{r};\;\;{\gamma_{\varphi r}} = {\gamma_{zr}} = 0;\;\;{\gamma_{z\varphi }} = {D_1}r $$

(B3)

The fiber in the composite (and even without the composite) is considered as infinitely long which means that there are no end effects and hence physical characteristics like strains and stresses cannot depend on the z-coordinate. Under such condition the stress equilibrium equations are

$$ \frac{{\partial {\sigma_r}}}{{\partial r}} + \frac{{{\sigma_r} - {\sigma_\varphi }}}{r} + \frac{1}{r}\frac{{\partial {\sigma_{\varphi r}}}}{{\partial \varphi }} = 0;\quad \frac{1}{r}\frac{{\partial {\sigma_\varphi }}}{{\partial \varphi }} + \frac{{\partial {\sigma_{\varphi r}}}}{{\partial r}} + 2\frac{{{\sigma_{\varphi r}}}}{r} = 0;\quad \frac{{\partial {\sigma_{zr}}}}{{\partial r}} + \frac{{{\sigma_{zr}}}}{r} + \frac{1}{r}\frac{{\partial {\sigma_{z\varphi }}}}{{\partial \varphi }} = 0 $$

(B4)

The applied load in this study is independent on the φ-coordinate. Hence, we can expect that stresses will not have this dependence either since there is no prioritised direction and even if the fiber is rotating, the response can not be φ-dependent. Under this assumption (B4) turns into

$$ \frac{{\partial {\sigma_r}}}{{\partial r}} + \frac{{{\sigma_r} - {\sigma_\varphi }}}{r} = 0;\;\;\frac{{\partial {\sigma_{\varphi r}}}}{{\partial r}} + 2\frac{{{\sigma_{\varphi r}}}}{r} = 0;\;\;\frac{{\partial {\sigma_{zr}}}}{{\partial r}} + \frac{{{\sigma_{zr}}}}{r} = 0 $$

(B5)

The conditions of zero tangential tractions on the internal boundary and on the external boundary of the sub-cylinder assembly give (in any sub-cylinder) ${\sigma_{zr}} \equiv {\sigma_{\varphi r}} \equiv 0$.

Appendix C

Solution for problem with r-dependent stress-strain state

Using the constitutive Eq. (1) in the first Eq. (B5) leads to

$$ {\bar Q_{23}}\frac{{d{\varepsilon_\varphi }}}{dr} + {\bar Q_{33}}\frac{{d{\varepsilon_r}}}{dr} + \frac{1}{r}\left[ {\left( {{{\bar Q}_{23}} - {{\bar Q}_{22}}} \right){\varepsilon_\varphi } + \left( {{{\bar Q}_{33}} - {{\bar Q}_{23}}} \right){\varepsilon_r}} \right] = \frac{1}{r}\left( {{{\bar Q}_{12}} - {{\bar Q}_{13}}} \right){\varepsilon_0} + \left( {{{\bar Q}_{26}} - 2{{\bar Q}_{36}}} \right){D_1} $$

(C1)

Substitute expressions from (B3) in (C1)

$$ \frac{{d{u_0}}}{{d{r^2}}} + \frac{1}{r}\frac{{d{u_0}}}{dr} - \frac{{{\alpha^2}}}{r^2}{u_0} = \frac{{{{\bar Q}_{12}} - {{\bar Q}_{13}}}}{{{{\bar Q}_{33}}}}\frac{{{\varepsilon_0}}}{r}\frac{{{{\bar Q}_{26}} - 2{{\bar Q}_{36}}}}{{{{\bar Q}_{33}}}}{D_1}\;\;{\text{where}}\;\;{\alpha^2} = \frac{{{{\bar Q}_{22}}}}{{{{\bar Q}_{33}}}} $$

(C2)

The general solution of Eq. (C2) is

$$ {u_0} = {A_1}{r^\alpha } + {A_2}{r^{ - \alpha }} + {\varepsilon_0}{a_1}r + {D_1}{a_2}{r^2} $$

(C3)

where

$$ \begin{array}{*{20}{c}} {{a_1} = \frac{{{{\bar Q}_{12}} - {{\bar Q}_{13}}}}{{{{\bar Q}_{33}}\left( {1 - {\alpha^2}} \right)}}} \hfill & {{a_2} = \frac{{{{\bar Q}_{26}} - 2{{\bar Q}_{36}}}}{{{{\bar Q}_{33}}\left( {4 - {\alpha^2}} \right)}}} \hfill \\ \end{array} $$

(C4)

For isotropic or transversely isotropic materials ${a_1} = {a_2} = 0$. Now strains may be calculated using (B3)

$$ {\varepsilon_r} = {A_1}\alpha {r^{\alpha - 1}} - {A_2}\alpha {r^{ - \alpha - 1}} + {\varepsilon_0}{a_1} + {D_1}2{a_2}r $$

(C5)

$$ {\varepsilon_\varphi } = {A_1}{r^{\alpha - 1}} + {A_2}{r^{ - \alpha - 1}} + {\varepsilon_0}{a_1} + {D_1}{a_2}r $$

(C6)

$$ {\gamma_{z\varphi }} = {D_1}r $$

(C7)

Expressions for stresses can be obtained using the constitutive Eq. (1)

$$ {\sigma_r} = {A_1}{\beta_1}{r^{\alpha - 1}} + {A_2}{\beta_2}{r^{ - \alpha - 1}} + {\varepsilon_0}{\beta_3} + {D_1}{\beta_4}r $$

(C8)

$$ {\sigma_\varphi } = {A_1}{\gamma_1}{r^{\alpha - 1}} + {A_2}{\gamma_2}{r^{ - \alpha - 1}} + {\varepsilon_0}{\gamma_3} + {D_1}{\gamma_4}r $$

(C9)

$$ {\sigma_z} = {A_1}{f_1}{r^{\alpha - 1}} + {A_2}{f_2}{r^{ - \alpha - 1}} + {\varepsilon_0}{f_3} + {D_1}{f_4}r $$

(C10)

$$ {\sigma_{z\varphi }} = {A_1}{g_1}{r^{\alpha - 1}} + {A_2}{g_2}{r^{ - \alpha - 1}} + {\varepsilon_0}{g_3} + {D_1}{g_4}r $$

(C11)

where

$$ {\beta_1} = {\bar Q_{23}} + \alpha {\bar Q_{33}},\;\,{\beta_2} = {\bar Q_{23}} - \alpha {\bar Q_{33}},\;\,{\beta_3} = {\bar Q_{13}} + \left( {{{\bar Q}_{23}} + {{\bar Q}_{33}}} \right){a_1},\;\,{\beta_4} = {\bar Q_{36}} + \left( {{{\bar Q}_{23}} + 2{{\bar Q}_{33}}} \right){a_2} $$

(C12)

$$ {\gamma_1} = {\bar Q_{22}} + \alpha {\bar Q_{23}}\;\;{\gamma_2} = {\bar Q_{22}} - \alpha {\bar Q_{23}}\;\;{\gamma_3} = {\bar Q_{12}} + \left( {{{\bar Q}_{22}} + {{\bar Q}_{23}}} \right){a_1}\;\;{\gamma_4} = {\bar Q_{26}} + \left( {{{\bar Q}_{22}} + 2{{\bar Q}_{23}}} \right){a_2} $$

(C13)

$$ {f_1} = {\bar Q_{12}} + \alpha {\bar Q_{13}}\;\;{f_2} = {\bar Q_{12}} - \alpha {\bar Q_{13}}\;\;{f_3} = {\bar Q_{11}} + \left( {{{\bar Q}_{12}} + {{\bar Q}_{13}}} \right){a_1}\;\;{f_4} = {\bar Q_{16}} + \left( {{{\bar Q}_{12}} + 2{{\bar Q}_{13}}} \right){a_2} $$

(C14)

$$ {g_1} = {\bar Q_{26}} + \alpha {\bar Q_{36}}\;\;{g_2} = {\bar Q_{26}} - \alpha {\bar Q_{36}}\;\;{g_3} = {\bar Q_{16}} + \left( {{{\bar Q}_{26}} + {{\bar Q}_{36}}} \right){a_1}\;\;{g_4} = {\bar Q_{66}} + \left( {{{\bar Q}_{26}} + 2{{\bar Q}_{36}}} \right){a_2} $$

(C15)