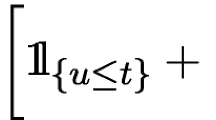Skip to main content
SpringerLink
Log in

A central limit theorem for convex sets

  • Published:
Inventiones mathematicae Aims and scope

Abstract

We show that there exists a sequence \(\varepsilon_n\searrow0\) for which the following holds: Let K⊂ℝn be a compact, convex set with a non-empty interior. Let X be a random vector that is distributed uniformly in K. Then there exist a unit vector θ in ℝn, t0∈ℝ and σ>0 such that

$$\sup_{A\subset\mathbb{R}}\left|\textit{Prob}\,\{\langle X,\theta\rangle\in A\}-\frac{1}{\sqrt{2\pi\sigma}}\int_Ae^{-\frac{(t - t_0)^2}{2\sigma^2}} dt\right|\leq\varepsilon_n,\qquad{(\ast)}$$

where the supremum runs over all measurable sets A⊂ℝ, and where 〈·,·〉 denotes the usual scalar product in ℝn. Furthermore, under the additional assumptions that the expectation of X is zero and that the covariance matrix of X is the identity matrix, we may assert that most unit vectors θ satisfy (*), with t0=0 and σ=1. Corresponding principles also hold for multi-dimensional marginal distributions of convex sets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Anttila, M., Ball, K., Perissinaki, I.: The central limit problem for convex bodies. Trans. Am. Math. Soc. 355(12), 4723–4735 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  2. Ball, K.: Logarithmically concave functions and sections of convex sets in ℝn. Stud. Math. 88(1), 69–84 (1988)

    MATH  Google Scholar 

  3. Bastero, J., Bernués, J.: Asymptotic behavior of averages of k-dimensional marginals of measures on ℝn. Preprint. Available at http://www.unizar.es/galdeano/preprints/2005/preprint34.pdf

  4. Bobkov, S.G.: On concentration of distributions of random weighted sums. Ann. Probab. 31(1), 195–215 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  5. Bobkov, S.G., Koldobsky, A.: On the central limit property of convex bodies. In: Geometric Aspects of Functional Analysis, Israel Seminar (2001–02). Lect. Notes Math., vol. 1807, pp. 44–52. Springer, Berlin (2003)

  6. Borell, C.: Convex measures on locally convex spaces. Ark. Mat. 12, 239–252 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  7. Brehm, U., Voigt, J.: Asymptotics of cross sections for convex bodies. Beitr. Algebra Geom. 41(2), 437–454 (2000)

    MATH  MathSciNet  Google Scholar 

  8. Brehm, U., Hinow, P., Vogt, H., Voigt, J.: Moment inequalities and central limit properties of isotropic convex bodies. Math. Z. 240(1), 37–51 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  9. Dasgupta, S., Gupta, A.: An elementary proof of a theorem of Johnson and Lindenstrauss. Random Struct. Algorithms 22(1), 60–65 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  10. Davidovič, J.S., Korenbljum, B.I., Hacet, B.I.: A certain property of logarithmically concave functions. Dokl., Akad. Nauk Azerb. 185, 1215–1218 (1969) (Russian). English translation in Sov. Math. Dokl. 10, 477–480 (1969)

  11. Diaconis, P., Freedman, D.: Asymptotics of graphical projection pursuit. Ann. Stat. 12(3), 793–815 (1984)

    MATH  MathSciNet  Google Scholar 

  12. Diaconis, P., Freedman, D.: A dozen de Finetti-style results in search of a theory. Ann. Inst. Henri Poincaré, Probab. Stat. 23(2), 397–423 (1987)

    MathSciNet  Google Scholar 

  13. Feller, W.: An Introduction to Probability Theory and its Applications, Volume II. John Wiley & Sons, Inc., New York, London, Sydney, (1971)

  14. Fradelizi, M.: Sections of convex bodies through their centroid. Arch. Math. 69(6), 515–522 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  15. Giannopoulos, A.A., Milman, V.D.: Euclidean structure in finite dimensional normed spaces. In: Handbook of the Geometry of Banach Spaces, Vol. I, pp. 707–779. North-Holland, Amsterdam (2001)

  16. Gordon, Y.: Gaussian processes and almost spherical sections of convex bodies. Ann. Probab. 16(1), 180–188 (1988)

    MATH  MathSciNet  Google Scholar 

  17. Gordon, Y.: On Milman’s inequality and random subspaces which escape through a mesh in ℝn. In: Geometric Aspects of Functional Analysis, Israel Seminar (1986–87). Lect. Notes Math., vol. 1317, pp. 84–106. Springer, Berlin (1988)

  18. Gromov, M.: Dimension, nonlinear spectra and width. In: Geometric Aspects of Functional Analysis, Israel Seminar (1986–87). Lect. Notes Math., vol. 1317, pp. 132–184. Springer, Berlin (1988)

  19. Grünbaum, B.: Partitions of mass-distributions and of convex bodies by hyperplanes. Pac. J. Math. 10, 1257–1261 (1960)

    MATH  Google Scholar 

  20. Hensley, D.: Slicing convex bodies – bounds for slice area in terms of the body’s covariance. Proc. Am. Math. Soc. 79(4), 619–625 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  21. Johnson, W.B., Lindenstrauss, J.: Extensions of Lipschitz mappings into a Hilbert space. In: Conference in Modern Analysis and Probability (New Haven, Conn., 1982). Contemp. Math. vol. 26, pp. 189–206. Am. Math. Soc. Providence, RI (1984)

  22. Klartag, B., Milman, V.D.: Geometry of log-concave functions and measures. Geom. Dedicata 112, 169–182 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  23. Klartag, B.: Uniform almost sub-gaussian estimates for linear functionals on convex sets. To appear in Algebra Anal. (St. Petersb. Math. J.)

  24. Koldobsky, A., Lifshits, M.: Average volume of sections of star bodies. In: Geometric Aspects of Functional Analysis, Israel Seminar (1996–00). Lect. Notes Math., vol. 1745, pp. 119–146. Springer, Berlin (2000)

  25. Ledoux, M.: Spectral gap, logarithmic Sobolev constant, and geometric bounds. Appears in: Eigenvalues of Laplacians and Other Geometric Operators. Surveys in Differential Geometry, vol. 9, pp. 219–240. Somerville, MA (2004)

  26. Leindler, L.: On a certain converse of Hölder’s inequality. Linear operators and approximation. Proc. Conf., Oberwolfach, (1971). Int. Ser. Numer. Math., vol. 20, pp. 182–184. Birkhäuser, Basel (1972)

  27. Lekkerkerker, C.G.: A property of Logarithmic concave functions I+II. Indag. Math., New Ser. 15, 505–521 (1953) (also known as Nederl. Akad. Wetensch. Proc. Ser. A. 56)

  28. Lindenstrauss, J.: Almost spherical sections; their existence and their applications. Jahresber. Dtsch. Math.-Ver. 39–61 (1992)

  29. Lovász, L., Vempala, S.: The geometry of logconcave functions and sampling algorithms. Random Struct. Algorithms (published online)

  30. Meckes, E.S., Meckes, M.W.: The central limit problem for random vectors with symmetries. Preprint.

  31. Milman, E.: On gaussian marginals of uniformly convex bodies. Preprint. Available at http://arxiv.org/abs/math.FA/0604595

  32. Milman, V.D.: A new proof of A. Dvoretzky’s theorem on cross-sections of convex bodies. Funkts. Anal. Prilozh. 5(4), 28–37 (1971) (Russian) English translation in Funct. Anal. Appl. 5, 288–295 (1971)

    Google Scholar 

  33. Milman, V.D.: Dvoretzky’s theorem – thirty years later. Geom. Funct. Anal. 2(4), 455–479 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  34. Milman, V.D., Pajor, A.: Isotropic position and inertia ellipsoids and zonoids of the unit ball of a normed n-dimensional space. In: Geometric Aspects of Functional Analysis, Israel Seminar (1987–88). Lect. Notes Math., vol. 1376, pp. 64–104. Springer, Berlin (1989)

  35. Milman, V.D., Schechtman, G.: Asymptotic Theory of Finite-Dimensional Normed Spaces. Lect. Notes Math., vol. 1200. Springer, Berlin (1986)

    MATH  Google Scholar 

  36. Naor, A., Romik, D.: Projecting the surface measure of the sphere of ℓ p n. Ann. Inst. Henri Poincaré, Probab. Stat. 39(2), 241–261 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  37. Paouris, G.: Concentration of mass and central limit properties of isotropic convex bodies. Proc. Am. Math. Soc. 133, 565–575 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  38. Paouris, G.: On the ψ2-behaviour of linear functionals on isotropic convex bodies. Stud. Math. 168(3), 285–299 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  39. Paouris, G.: Concentration of mass on isotropic convex bodies. C. R. Math. Acad. Sci., Paris 342(3), 179–182 (2006)

    MATH  MathSciNet  Google Scholar 

  40. Paouris, G.: Concentration of mass in convex bodies. Geom. Funct. Anal. 16(5), 1021–1049 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  41. Pisier, G.: The volume of convex bodies and Banach space geometry. In: Cambridge Tracts in Mathematics, vol. 94. Cambridge University Press, Cambridge (1989)

  42. Prékopa, A.: Logarithmic concave measures with application to stochastic programming. Acta Sci. Math. 32, 301–316 (1971)

    MATH  Google Scholar 

  43. Prékopa, A.: On logarithmic concave measures and functions. Acta Sci. Math. 34, 335–343 (1973)

    MATH  Google Scholar 

  44. Romik, D.: Randomized Central Limit Theorems – Probabilisitic and Geometric Aspects. PhD dissertation. Tel-Aviv University (2001)

  45. Schechtman, G.: A remark concerning the dependence on ε in Dvoretzky’s theorem. In: Geometric Aspects of Functional Analysis, Israel Seminar (1987–88). Lect. Notes Math., vol. 1376, pp. 274–277. Springer, Berlin (1989)

  46. Schechtman, G.: Two observations regarding embedding subsets of Euclidean spaces in normed spaces. Geom. Funct. Anal. 200, 125–135 (2006)

    MATH  MathSciNet  Google Scholar 

  47. Schoenberg, I.J.: On Pólya frequency functions. I. The totally positive functions and their Laplace transforms. J. Anal. Math. 1, 331–374 (1951)

    Google Scholar 

  48. Sodin, S.: Tail-sensitive gaussian asymptotics for marginals of concentrated measures in high dimension. To appear in: Geometric Aspects of Functional Analysis, Israel Seminar. Lect. Notes Math. Available at http://arxiv.org/abs/math.MG/0501382

  49. Stein, E.M., Weiss, G.: Introduction to Fourier analysis on Euclidean spaces. Princeton Mathematical Series, no. 32. Princeton University Press, Princeton, NJ (1971)

  50. Stroock, D.W.: Probability Theory, an Analytic View. Cambridge University Press, Cambridge (1993)

    MATH  Google Scholar 

  51. Sudakov, V.N.: Typical distributions of linear functionals in finite-dimensional spaces of high-dimension. Dokl., Akad. Nauk Azerb. 243(6), 1402–1405 (1978) (Russian) English translation in Sov. Math. Dokl. 19, 1578–1582 (1978)

  52. von Weizsäcker, H.: Sudakov’s typical marginals, random linear functionals and a conditional central limit theorem. Probab. Theory Relat. Fields 107(3), 313–324 (1997)

    Article  MATH  Google Scholar 

  53. Wojtaszczyk, J.O.: The square negative correlation property for generalized orlicz balls. To appear in: Geometric Aspects of Functional Analysis, Israel Seminar. Lect. Notes Math.

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Princeton University, Princeton, NJ, 08544, USA

    B. Klartag

Authors
  1. B. Klartag
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to B. Klartag.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Klartag, B. A central limit theorem for convex sets. Invent. math. 168, 91–131 (2007). https://doi.org/10.1007/s00222-006-0028-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00222-006-0028-8

Keywords

Search

Navigation