FormalPara Key Points

To inform decision making in the ritlecitinib (an inhibitor of JAK3/TEC family kinases) program, where dose-ranging and confirmatory evidence of efficacy were generated in a single clinical trial, longitudinal exposure–response (ER) modeling was conducted to evaluate ritlecitinib efficacy in patients with alopecia areata, based on Severity of Alopecia Tool score data using a continuous bounded outcome (CBO) modeling approach.

The CBO modeling and simulation addressed contextualization of the ritlecitinib ER relationship and loading dose effect to guide dose selection, understanding of variability in efficacy due to covariates, and the impact of temporary treatment interruption on ritlecitinib efficacy.

This CBO modeling approach can be applied to many indications where efficacy is measured on a bounded scale to enable decision making in the accelerated drug development paradigm.

1 Introduction

Model-informed drug development (MIDD) is a powerful approach that uses quantitative modeling and simulation tools to support drug development and decision making. Since the MIDD concept was introduced in the 2004 Critical Path Initiative by the Food and Drug Administration (FDA) [1], application of MIDD has been expanded to include various stages of drug development, and the role of MIDD approaches has been increasingly recognized to help reduce the time and cost of drug development [2]. Especially in drug development programs with compressed timelines, the role of MIDD becomes critical for contextualizing existing and accruing new information, filling in knowledge gaps, and facilitating decision making.

Ritlecitinib is an orally bioavailable, small molecule drug that irreversibly inhibits Janus kinase 3 (JAK3) and tyrosine kinase expressed in hepatocellular carcinoma (TEC) family kinases [3]. Treatment with ritlecitinib is predicted to inhibit the inflammatory pathways mediated by interleukin (IL)-7, IL-15, and IL-21, which have been implicated in the pathogenic pathways of alopecia areata (AA) [4]. The proof of concept for ritlecitinib in the treatment of AA has been demonstrated in a phase 2a study (NCT02974868) [5]. Without a separate dose-ranging phase 2b study, the development program moved to a combined phase 2b/3 study that served both as a dose-ranging and single pivotal study. Therefore, understanding of dose/exposure–response (ER) relationships, dose and regimen optimization, and demonstration of long-term treatment benefit were all evaluated within a single trial.

Here, an example of MIDD is provided, where modeling and simulation helped facilitate decision making in an accelerated drug development program. A longitudinal ER analysis was conducted to evaluate the efficacy of ritlecitinib in patients with AA, using the absolute Severity of Alopecia Tool (SALT) score data from all phase 2 and 3 studies (B7931005, B7981015, and B7981032). The SALT score is measured on a bounded scale (0–100) and therefore presents a technical challenge in model development due to the highly skewed distribution of the data, including a significant proportion of boundary data points [6]. This paper discusses an application of pharmacometric methodology to describe the continuous bounded outcome (CBO) data of SALT scores in the ritlecitinib program and utilization of CBO modeling and simulation for drug development decision making.

2 Methods

2.1 Study Design

This analysis was conducted on pooled data from three clinical studies (B7931005, B7981015, and B7981032). B7931005 was a phase 2a study to investigate ritlecitinib and brepocitinib in adults with AA with 50% or greater scalp hair loss (NCT02974868). The study consisted of three periods: a 24-week double-blind treatment period, an up to 48-week single-blind extension (SBE) period, and a 24-week extension period. Only the initial 24-week period and SBE period of ritlecitinib and placebo data were included in the analysis. In the first period, ritlecitinib 200 mg once daily (QD) for 4 weeks followed by ritlecitinib 50 mg QD for 20 weeks and matching placebo were administered. The SBE period started after a 4-week drug holiday. In the SBE period, responders with a ≥ 30% change from baseline (CFB) received placebo until they met the re-treatment criterion (% CFB at week 24 − % CFB post week 24 > 30%) and then were re-treated with ritlecitinib 200 mg QD for 4 weeks, followed by 50 mg QD. Non-responders received another course of ritlecitinib 200 mg QD for 4 weeks, followed by 50 mg QD for 20 weeks.

B7981015 was a phase 2b/3 study to investigate the efficacy and safety of ritlecitinib in adults and adolescents with AA (≥ 12 years) with 50% or greater scalp hair loss (NCT03732807). The treatment period comprised a 24-week placebo-controlled period followed by a 24-week extension phase. Eligible participants were randomized in a 2:2:2:2:1:1:1 manner to the following treatments: (1) ritlecitinib 200 mg QD for 4 weeks, followed by ritlecitinib 50 mg QD for 44 weeks; (2) ritlecitinib 200 mg QD for 4 weeks, followed by ritlecitinib 30 mg QD for 44 weeks; (3) ritlecitinib 50 mg QD for 48 weeks; (4) ritlecitinib 30 mg QD for 48 weeks; (5) ritlecitinib 10 mg QD for 48 weeks; (6) placebo for 24 weeks → ritlecitinib 200 mg QD for 4 weeks, followed by ritlecitinib 50 mg QD for 20 weeks; and (7) placebo for 24 weeks → ritlecitinib 50 mg QD for 24 weeks.

B7981032 was a phase 3 long-term study to evaluate the safety and efficacy of ritlecitinib in adults and adolescents with AA (≥ 12 years) with 25% or greater scalp hair loss (NCT04006457). All eligible participants enrolled in study B7981032 after participation in either B7931005 or B7981015 received ritlecitinib 50 mg QD. All de novo participants received ritlecitinib 200 mg QD for 4 weeks, followed by ritlecitinib 50 mg QD. Since the B7981032 study was not completed at the time of this analysis, the only available datacut at the time of modeling analysis was included in the analysis dataset.

All the studies were conducted in accordance with the Declaration of Helsinki and the principles of Good Clinical Practice. The final protocols were approved by the institutional review boards.

2.2 Study Assessment

Sparse pharmacokinetics (PK) samples were collected in all studies. The exposure metric was derived from empirical Bayes estimates (EBEs) of the final population PK model [7]. Average drug concentration (Cavg) during the time interval between previous SALT record and the current SALT record was calculated based on the patient’s dosing diary, to be used as the exposure metric for ER analysis.

SALT is a quantitative assessment of AA severity that captures percentage hair loss and was consistently collected as an efficacy endpoint in all studies [8]. The SALT score assessment schedule for each study is available in Supplementary Table S1 (see the electronic supplementary material). The score ranges from 0 to 100, where 100 represents complete hair loss and 0 represents no hair loss.

2.3 ER Analysis

The pharmacometric methodology of CBO analysis proposed by Hutmacher et al. was adapted and modified [9]. The non-boundary data were first scaled between 0 and 1, and a transformation family of Aranda-Ordaz functions was applied to help normalize the skewed distribution of CBO data as follows:

$$\begin{aligned} z & = \frac{{\left( {100 - y} \right) - 0}}{100 - 0}, z \in \left( {0,1} \right) \\ x & = h\left( {y,\alpha } \right) = \log \left[ {\frac{{\left( {1 - z} \right)^{ - \alpha } - 1}}{\alpha }} \right], \alpha \ne 0, \\ \end{aligned}$$
(1)

where \(y\) is the observation in the SALT scale and \(x\) is the observation in the transformed scale. The transformation factor α was estimated during model fitting.

A general nonlinear mixed-effects model was then constructed based on the transformed response:

$$x\left| {\eta = h\left( {y,\alpha } \right)} \right|\eta = \mu \left( \eta \right) + \sigma \cdot \varepsilon ,$$
(2)

where x|η represents x conditioning on a vector of subject-specific random effects η, μ(η) is a conditional mean, σ is the residual error magnitude, and ε is the residual random error, which is assumed to be normally distributed with mean 0 and variance 1. The conditional mean μ(η) was modeled as:

$$\mu \left( \eta \right) = f_{b} \left( \eta \right) - f_{{{\text{placebo}}}} \left( t \right) - f_{{{\text{drug}}}} \left( t \right),$$
(3)

where \({f}_{b}\) is the baseline as a function of fixed effects (BASE) and random effects (η) [BASE + η], \({f}_{{\text{placebo}}}(t)\) is the placebo effect function, and \({f}_{{\text{drug}}}(t)\) is the drug effect function.

The placebo effect model was developed first, and then the drug effect model was added to the selected placebo effect model. For both placebo and drug effect functions, an indirect response model was considered using a latent variable approach to handle the delayed onset and offset of the response [10]:

$$\begin{aligned} f_{{{\text{placebo}}}} \left( t \right) & = {\text{PBO}}\left( t \right) - \frac{{k_{{{\text{in}}1}} }}{{k_{{{\text{out}}1}} }}, f_{{{\text{drug}}}} \left( t \right) = E\left( t \right) - \frac{{k_{{{\text{in}}2}} }}{{k_{{{\text{out}}2}} }} \\ \frac{{{\text{dPBO}}\left( t \right)}}{{{\text{d}}t}} & = k_{{{\text{in}}1}} \cdot \left[ {1 + I_{{{\text{PBO}}}} \cdot P_{{{\text{max}}}} } \right] - k_{{{\text{out}}1}} \cdot {\text{PBO}}\left( t \right) \\ \frac{{{\text{d}}E\left( t \right)}}{{{\text{d}}t}} & = k_{{{\text{in}}2}} \cdot \left[ {1 + \frac{{E_{{{\text{max}}}} \cdot C_{{{\text{avg}}}} \left( t \right)}}{{{\text{EC}}_{50} + C_{{{\text{avg}}}} \left( t \right)}}} \right] - k_{{{\text{out}}2}} \cdot E\left( t \right) \\ {\text{PBO}}\left( {t = 0} \right) & = \frac{{k_{{{\text{in}}1}} }}{{k_{{{\text{out}}1}} }}, E\left( {t = 0} \right) = \frac{{k_{{{\text{in}}2}} }}{{k_{{{\text{out}}2}} }}, \\ \end{aligned}$$
(4)

where \({\text{PBO}}(t)\) and \(E\left(t\right)\) are latent variables, \({I}_{{\text{PBO}}}\) is an indicator variable that equals 1 if treatment was given and equals 0 otherwise, \({P}_{{\text{max}}}\) is the maximum placebo effect, \({E}_{{\text{max}}}\) is the maximum effect, \({k}_{{\text{in}}}\) and \({k}_{{\text{out}}}\) are rate constants determining a delay between placebo or drug treatment and response, and \({{\text{EC}}}_{50}\) represents the Cavg yielding half of \({E}_{{\text{max}}}\). \({k}_{{\text{in}}}\) and \({k}_{{\text{out}}}\) were parameterized as \(\frac{{\text{ln}}2}{{t}_{1/2}}\), such that the rate constant of \({k}_{{\text{in}}}\) and \({k}_{{\text{out}}}\) can be viewed in the unit of time (\({t}_{1/2}\) was estimated instead of \({k}_{{\text{in}}}\) or \({k}_{{\text{out}}}\)).

Data on the boundaries, 0 or 100, were treated as censored data when constructing the likelihood. The interpretation of censoring is similar to that in PK and pharmacodynamic (PD) assays in that if a more sensitive way of measurement were available, values of 0 or 100 would not have been observed. The likelihoods of 0 observations being less than the minimum observable non-zero value and 100 observations being greater than the maximum observable non-hundred value were estimated, such that the likelihood for all the data is maximized in the model development.

Inter-individual variability (IIV) was incorporated in BASE, \({E}_{{\text{max}}}\), and \({k}_{{\text{in}}2}\)/\({k}_{{\text{out}}2}\) using a multiplicative exponential error model (\({P}_{i}={P}_{{\text{pop}}}\bullet {\text{exp}}({\eta }_{i})\) for ith individual) and \({P}_{{\text{max}}}\) with an additive model (\({P}_{i}={P}_{{\text{pop}}}+{\eta }_{i}\)) to allow both disease worsening and improving.

The covariates tested were effects of sex, weight, age, race, region, disease severity (alopecia totalis [AT]/alopecia universalis [AU] status), and prior treatment on BASE; sex, weight, age, race, region, disease severity, prior treatment, AA duration since first diagnosis (DURF), duration of current AA episode (DURC), and baseline SALT score on \({E}_{{\text{max}}}\); and age, weight, region, disease severity, prior treatment, DURF, and DURC on \({k}_{{\text{in}}2}\)/\({k}_{{\text{out}}2}\). Stepwise covariate analysis was performed using both forward addition (p < 0.05) and backward elimination (p < 0.001).

Model adequacy was evaluated through changes in objective function value (OFV), visual inspection of diagnostic plots, precision of the parameter estimates, and decreases in IIV and residual variability. The final model was further evaluated for its predictive performance by visual predictive check (VPC).

ER analyses were performed using NONMEM version 7.5.0. Exploratory analyses, diagnostic plots, post-processing of NONMEM output, and simulations were performed with R version 4.0.3. Perl-speaks-NONMEM (PsN) version 5.2.6 was used for performing sampling importance resampling (SIR). The NONMEM analyses were conducted using the Laplace estimation method with interaction and ADVAN13 with TOL = 6. The stochastic approximation expectation maximization (SAEM) method with importance sampling (IMP) was used for the estimation algorithm.

2.4 Clinical Trial Simulation to Understand Full Dose-Response Based on Limited Dose Range Data

To better understand translation of the established ER relationship in the transformed scale into the original SALT scale, clinical trial simulation was performed for various QD doses. One thousand datasets of longitudinal SALT scores for 130 participants, an average sample of the single arms of the B7981015 study (n = 129–132), were simulated for placebo, 30-, 50-, 100-, 200-, 400-, and 600-mg ritlecitinib QD dosage regimens. The demography of the 130 participants was assumed to be identical to that of the 50-mg arm of study B7981015. For each trial simulation, PK profiles were simulated first using EBEs for the 50-mg arm from the PK model, and SALT profiles were then simulated using a parameter set randomly drawn from a multivariate normal distribution using the population estimates and corresponding variance–covariance matrix of the estimates from the final CBO model. The SALT scores were simulated based on the transformed scale first and then back-transformed into the original SALT scale. Both PK concentrations and SALT scores including residual variability were simulated every week up to week 48, and placebo-adjusted responder rates for SALT ≤ 20 at week 24 and week 48 were collected for each simulated trial. The median and 95% prediction interval (PI) of the placebo-adjusted responder rates from 1000 simulated trials were summarized for each dosage regimen.

2.5 Clinical Trial Simulation to Understand Loading Dose Effect

The purpose of this simulation was to delineate the loading dose effect on clinical onset of response as well as overall outcome. The simulation scheme was identical to that of the previous simulation except the explored dosing regimens. One thousand datasets of longitudinal SALT scores for 130 participants were simulated for placebo, 30 mg QD, 50 mg QD, and 200 mg QD for 4 weeks, followed by 30 mg QD and 200 mg QD for 4 weeks, followed by 50-mg QD dosage regimens. The SALT score was simulated for every week up to week 48 to correctly capture the onset of response. In study B7981015, the clinical onset was defined as the time when the responder rate for SALT ≤ 20 separated from placebo based on 95% confidence interval (CIs). Therefore, simulation results were summarized based on the placebo-adjusted SALT ≤ 20 responder rate, to evaluate when the lower bound of the 95% CI for placebo-adjusted responder rate became > 0. Since clinical onset based on this definition would be influenced by sample size, clinical trial simulation was conducted using the same sample size for the single arm of B7981015 (n = 130).

2.6 Clinical Trial Simulation to Evaluate Treatment Interruption Effect

Simulation was conducted to assess the impact of treatment interruption on loss of efficacy, SALT ≤ 20, after patients achieve a stable response. The study participants for the simulation were assumed to be identical to participants in study B7981015 (n = 715), and longitudinal SALT scores for each individual were simulated based on EBEs of final model parameters. In this simulation, all the participants were treated with 50 mg QD until week 96 to ensure the SALT response had reached a plateau, and SALT scores were simulated for every week up to week 144 (48 weeks after treatment withdrawal) to capture any changes of SALT score after treatment interruption. For responders, defined as participants achieving SALT ≤ 20 at week 96, time to lose SALT ≤ 20 response was collected and the proportions of responders losing SALT ≤ 20 response at various treatment interruptions with durations of 4, 6, 8, 10, 12, 14, 16, 24, 36, and 48 weeks were summarized.

3 Results

3.1 Observed Data Summary

The final analysis dataset included 11,857 observations from 1268 patients. The baseline characteristics are summarized in Table 1. Continuous covariates are further summarized by disease severity. The distribution of continuous covariates was relatively similar between patients with non-AT/AU (the “non-AT/AU group”) and patients with AT/AU (the “AT/AU group”) except the baseline SALT score and disease duration for the current episode. The AT/AU group had baseline SALT scores of 100 by definition of disease classification, whereas the non-AT/AU group had baseline scores < 100. The AT/AU group also had a relatively longer duration of disease for the current episode compared with the non-AT/AU group.

Table 1 Summary of baseline characteristics in the analysis data
Full size table

3.2 Final ER Model

The final placebo model included three transit compartments in addition to the initial indirect response model in Eq. 4 to describe the delayed response. The entire model development history is available in Supplementary Table S2 (see the electronic supplementary material). Separate \({k}_{{\text{in}}1}\) and \({k}_{{\text{out}}1}\) estimation was not supported; hence, \({k}_{{\text{in}}1}\) was assumed to be the same as \({k}_{{\text{out}}1}\). Since baseline SALT scores were different between non-AT/AU and AT/AU, disease severity (non-AT/AU vs AT/AU) was incorporated as a structural covariate on BASE.

The final drug effect model was an \({E}_{{\text{max}}}/{{\text{EC}}}_{50}\) model with two transit compartments to describe the delayed response. Separate \({k}_{{\text{in}}2}\) and \({k}_{{\text{out}}2}\) estimation was not supported; hence, \({k}_{{\text{in}}2}\) was assumed to be the same as \({k}_{{\text{out}}2}\). The model run separately estimating \({k}_{{\text{in}}2}\) and \({k}_{{\text{out}}2}\) was completed without producing a covariance step, indicating that the model may be overparameterized. Study B7981032 effect on BASE was incorporated to address differences in inclusion criteria between studies (baseline SALT ≥ 50 for B7931005 and B7981015 vs baseline SALT ≥ 25 for B7981032). AT/AU effects on \({P}_{{\text{max}}}\) and \({k}_{{\text{out}}2}\) were additionally included as structural covariates to better describe AT/AU response.

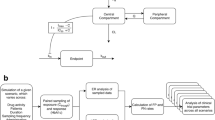
The selected base model with both placebo and drug effect includes IIV on BASE, \({P}_{{\text{max}}}\), \({E}_{{\text{max}}}\), or \({k}_{{\text{out}}2}\) parameters. After the base model selection, covariate effects on the base ER model parameters were graphically examined with inter-individual random effect on BASE, \({E}_{{\text{max}}}\), or \({k}_{{\text{out}}2}\) vs covariate plots. There were no strong correlations observed on any of the plots (Figs. S1–S3, see the electronic supplementary material). In line with this, the forward addition step of covariate analysis did not identify any important covariates. Therefore, the final base model was the selected final model. The schematic diagram of the final model is presented in Fig. 1.

Fig. 1
figure 1

Schematic diagram of longitudinal exposure–response model for SALT score. \({k}_{{\text{in}}}\) and \({k}_{{\text{out}}}\) are rate constants determining a delay between placebo or drug treatment and response, \({P}_{{\text{max}}}\) is the maximum placebo effect, \({I}_{{\text{PBO}}}\) is an indicator variable that = 1 if treatment was given and = 0 otherwise, \({E}_{{\text{max}}}\) is the maximum drug effect, \({{\text{EC}}}_{50}\) represents the PK exposure (Cavg(t)) yielding half of \({E}_{{\text{max}}}\), and SALT* represents SALT score in transformed scale. Cavg average drug concentration, PK pharmacokinetics, SALT Severity of Alopecia Tool

Full size image

Parameter estimates and SIR results of the final model are presented in Table 2. Asymptotic 95% CI and SIR 95% CI were very similar and demonstrated all the parameters were estimated with acceptable precision. Baseline values were different based on the disease severity and study, with a population mean of 1.92 (87.4% in original scale) for the non-AT/AU group in B7931005 and B7981015, 0.68 (67.3% in original scale) for the non-AT/AU group in B7981032, and 11.6 (100%) for the AT/AU group. The \({P}_{{\text{max}}}\) parameter was not precisely estimated for the non-AT/AU group and therefore was fixed to zero, whereas a small positive placebo effect was estimated for the AT/AU group. The \({P}_{{\text{max}}}\) estimate of 2.75 in the transformed scale did not induce any changes in SALT score for the AT/AU group, due to their large baseline value.

Table 2 Parameter estimates and SIR results of the final model
Full size table

The \({E}_{{\text{max}}}\) parameter estimate was 15.8 in the transformed scale for both non-AT/AU and AT/AU groups, which is translated into a complete recovery in SALT score (SALT score of 0 for non-AT/AU group and 0.33 for AT/AU group). The \({k}_{{\text{out}}2}\) estimate in half-life was smaller for the AT/AU group (3.11 weeks for AT/AU vs 7.80 weeks for non-AT/AU, which translates to mean transit time (\(\frac{\#\mathrm{ of transit}+1}{{k}_{{\text{out}}2}}\)) of 13.5 weeks vs 33.8 weeks, respectively), but the quicker onset in the AT/AU group was offset by their higher baseline, which requires a large change in SALT score to reach meaningful clinical response. The \({{\text{EC}}}_{50}\) estimate was a Cavg of 53.6 ng/mL, similar to the Cavg of 50 mg QD (52 ng/mL).

The model diagnostics are presented in Fig. 2. The transformation factor (α) was estimated to be 1.19 (Table 2), which adjusted the skewed distribution of the data to be normally distributed (Fig. 2A). The percentages of the boundary score were 5.39% for SALT = 0 and 24.9% for SALT = 100 in observed data, and 5.74% (95% CI 4.84–6.67) for SALT = 0 and 24.6% (95% CI 23.0–26.2) for SALT = 100 in the simulated data, indicating that the censored model was able to predict the percentage of boundary data adequately (Fig. 2B). Lastly, the model was developed for raw SALT score, but the VPC plot (Fig. 2C) showed generally good agreement between observed data and simulated data based on responder rate for SALT ≤ 20, which was the primary endpoint of the pivotal study.

Fig. 2
figure 2

Diagnostic plots. A Distribution of observed data excluding boundary values in original vs transformed scale. B Percentage of bounded outcomes for observed vs simulated data. C Visual predictive check of the final model in terms of responder rate for SALT ≤ 20. The black line represents the observed placebo-adjusted responder rate up to week 24 and observed responder rate after week 24, and the gray shaded region represents the 95% prediction interval from the final model for the corresponding endpoint. The dotted lines represent median prediction from the final model for the corresponding endpoint. The dashed lines represent when the non-placebo-controlled period (week 24) and B7981032 study (week 48) started. CI confidence interval, PBO placebo, SALT Severity of Alopecia Tool, wk week

Full size image

3.3 Clinical Trial Simulation to Understand Full Dose-Response Based on Limited Dose Range Data

The simulation results for the placebo-adjusted SALT ≤ 20 responder rate at various QD doses are presented in Fig. 3. Simulation was conducted for a dosage range of 30–600 mg QD to illustrate where the tested dosages in B7981015 are located on the ER curve. Based on simulation results from the ER relationship established in the CBO model, higher efficacy is expected at doses greater than 50 mg, with dosages of 400 mg QD approaching the maximum efficacy.

Fig. 3
figure 3

Placebo-adjusted responder rate for SALT ≤ 20 at week 24 and week 48 for various QD doses. Error bars represent 95% prediction intervals. QD once a day, SALT Severity of Alopecia Tool

Full size image

3.4 Clinical Trial Simulation to Understand Loading Dose Effect

The simulation results are visually presented in Fig. 4 for loading (200/30 mg or 200/50 mg QD) and non-loading (30 mg or 50 mg QD) dosage regimens. For the comparison, the PK profiles of those regimens are also presented in the top panel of Fig. 4. As expected from the small half-life of ritlecitinib (~2 h), PK exposures quickly reached the new steady state after the loading dose was switched to the maintenance dose at week 4. In contrast, the loading dose effect stayed longer in clinical efficacy, thereby resulting in greater efficacy for the loading dose regimen than the non-loading dose regimen at week 24, when the primary endpoint was measured in study B7981015. The simulation results indicated that the loading dose achieved the clinical onset of SALT ≤ 20 seven weeks faster for the 30-mg QD group (6 vs 13 weeks) and 3 weeks faster for the 50-mg QD group (6 vs 9 weeks). However, the initial quicker response was not sustained and did not translate into higher response rates long term, such that the 95% CIs of responder rates were largely overlapped between loading and non-loading dose regimens at week 48.

Fig. 4
figure 4

Evaluation of the loading dose effect on the clinical onset of efficacy when PD half-life is long. Top figures represent the PK profile of loading vs non-loading dosing regimens as geometric mean Caverage, and middle figures represent the efficacy profile of loading vs non-loading regimens as median placebo-adjusted responder rate with 95% confidence intervals. Bottom figures represent the efficacy profile of loading vs non-loading regimens for the initial 24 weeks. Caverage average drug concentration, PD pharmacodynamic, PK pharmacokinetics, POP population, wk week

Full size image

3.5 Clinical Trial Simulation to Evaluate Treatment Interruption Effect

The analysis data included limited information from the SBE period of study B7931005 that could demonstrate SALT score change after treatment withdrawal and re-treatment. Randomly selected individual model fits for the SBE period data of study B7931005 are presented in Fig. 5A, demonstrating that the final model well described all the initial response to treatment, treatment withdrawal, and re-treatment data.

Fig. 5
figure 5

Randomly selected individual model fit to support treatment interruption simulation. A Individual model fit for study B7931005 where both drug onset and offset information is available. B Example of predicted individual SALT score profiles after treatment interruption. The black circles are observations, and the green lines are model predictions. The red lines represent the week 96 time point when treatment interruption starts. QD once a day, SALT Severity of Alopecia Tool, wk week

Full size image

Based on this finding, SALT score profiles after treatment withdrawal were predicted using EBEs of the final model for all B7981015 study patients, as seen in the example profiles of Fig. 5B. The proportion of responders losing SALT ≤ 20 response after treatment withdrawal was further summarized according to the duration of treatment interruption (Table 3). Results indicated that the risk of losing SALT ≤ 20 response is very low (i.e., < 10%) with treatment interruption of ≤ 6 weeks, and 70% of patients are predicted to lose SALT ≤ 20 response with 48 weeks of treatment interruption.

Table 3 Predicted proportion of responders losing SALT ≤ 20 response for various dose interruption durations
Full size table

4 Discussion

The analysis in this paper characterized the longitudinal ER relationship of ritlecitinib efficacy in patients with AA using CBO modeling analysis. The description of CBO modeling strategy and how the established model informed decision making in the accelerated drug development program are discussed below.

4.1 Application of Pharmacometrics Methodology to Describe CBO Data

Bounded scales are commonly used to assess disease status and in turn used as clinical efficacy endpoints in clinical trials. Examples of such scales are the Psoriasis Area and Severity Index (0–72) [11], Disability Assessment for Dementia (0–100) [12], and Functional Assessment Questionnaire (0–30) [13]. Several pharmacometric modeling methodologies have been proposed to handle CBO data [9, 14,15,16]. In the current analysis, a censoring approach with transformation of non-boundary data proposed by Hutmacher et al. [9] was utilized due to its flexibility in handling boundary values, which consist of almost 30% of the analysis data. The developed model adequately adjusted the skewed distribution of the data and well described the longitudinal SALT score profile of ritlecitinib as well as the frequency of the boundary data.

The developed CBO model also utilized a latent variable indirect response modeling approach. The indirect response model is a widely used semi-mechanistic framework to link PD responses to PK exposure when there is a delay between PK exposure and PD responses. However, if the PD endpoint is a categorical or bounded outcome variable, the PD responses cannot be used as a raw scale for a dependent variable of PKPD modeling. To be applicable for such cases, the latent variable approach was developed, which links PD responses with drug exposure through an unobservable latent variable in the indirect response model framework [17]. In this modeling, the drug effect is assumed to be driven by a fluctuation of unobservable latent variable. Ritlecitinib irreversibly inhibits JAK3/TEC family kinases [3], and the improvement in SALT score is the gradual outcome of their modulation on the downstream signaling pathways. Therefore, the latent variable can be considered as a summation of all of ritlecitinib’s downstream effects, which eventually affect hair follicles to exhibit scalp hair growth.

The Cavg during the time interval between previous SALT score and the current SALT score was used as the PK exposure metric driving efficacy in the current analysis. The individual post-hoc concentration estimates could not be used due to the impractical long run time (> 150 h), and the summary measure of PK exposure was considered instead to complete the analysis in time. The Cavg has been widely used as a predictive PK exposure metric of PD response, unless the PD effect is acute (e.g., maximum concentration [Cmax] is the key driver for drug-induced QT prolongation) or sustained inhibition of the target determines the PD effect (minimum concentration is the key driver of efficacy for antibiotic drugs) [18]. Given that ritlecitinib irreversibly inhibits JAK3/TEC family kinases [3] and the improvement in SALT score is the gradual outcome of their modulation on the downstream signaling pathways, it is reasonable to assume that the efficacy is not sensitive to the short-term fluctuation in exposure such as Cmax and is rather influenced by average exposure over a period of time (i.e., Cavg) [19]. The selected PK exposure metric, Cavg during the time interval of the adjacent two SALT scores, has an advantage over steady-state Cavg calculated solely based on dose and clearance, which is often considered as the first choice of exposure metric in ER analyses. This metric can account for PK exposure fluctuation due to, e.g., treatment interruptions, and therefore can be considered as an acceptable surrogate for concentration when technical challenge is expected with using concentration for ER analyses.

4.2 Utilization of CBO Analysis for Drug Development Decision Making

Understanding of the ER relationship based on CBO analysis justified the single pivotal trial strategy. The CBO analysis results showed the EC50 estimate was 53.6 ng/mL, similar to the Cavg of 50 mg QD, suggesting that the tested dose range is in the ascending part of the entire dose-response relationship. By establishing EC50 estimates based on a totality of information from all the patient studies, the analysis demonstrated ritlecitinib exposure-dependent efficacy increase, which provides a causal confirmation of treatment effect of ritlecitinib in patients with AA. The causal evidence of effectiveness supports utilization of a single pivotal trial, in addition to empiric confirmation of treatment effect at a stringent α level of 0.00125 in study B7981015 [20, 21].

The CBO analysis guided dose selection by contextualizing study findings. The loading dose of 200 mg was evaluated in study B7981015 based on the hypothesis that maximal inhibition of the immunomodulatory pathways at initiation of treatment can accelerate clinical response, which can be maintained by subsequent lower maintenance doses. The loading dose is usually considered when the PK half-life of a drug is long and there is a need to accelerate the time to reach the target drug concentration. In inflammatory diseases, a loading dose was considered to address high inflammatory load in the active initial phase even though translation of high exposure into better clinical outcome has not been clearly established [22]. The CBO model-based evaluation based on study data indicates that the loading dose effect was on accelerating the onset of efficacy, with no long-term benefit, due to a combination of long PD half-life and ascending region of dose-response for the tested dose range. Both loading and non-loading dose regimens eventually reached their maintenance dose–level efficacy, which is in line with pharmacological first principles of a concentration-driven pharmacological response. Given that AA is not a life-threatening disease and need for both loading and maintenance doses creates complexity in prescribing, dispensing, and administration, contextualization of a loading dose using a CBO model aided selection of a non-loading dose regimen, 50 mg QD, as the proposed registrational dose.

The disease severity was the only important covariate identified in the current analysis, with no other covariates that could explain the variability in the efficacy. The DURC has been hypothesized to influence the treatment response, where patients whose current AA episode has lasted > 10 years are less likely to respond to treatment [23]. However, no obvious trend was observed in the DURC and the efficacy parameters. The study inclusion criteria for B7981015 and B7981032 restricted the duration for the current episode of hair loss to ≤ 10 years, which may have contributed to the above observation. Overall, ritlecitinib efficacy was lower in patients with AT/AU than in patients without AT/AU, consistent with what was reported in multiple other studies [24, 25]. The model explained this efficacy difference with large baseline difference between the non-AT/AU and AT/AU groups (1.92 vs 11.6) in the transformed scale, which cannot be captured in the SALT scale (87.4% vs 100%). The drug effect is additive to the baseline based on the transformed scale in the model, and therefore, the same PK exposure is expected to result in different efficacy between the non-AT/AU and AT/AU groups according to their baseline values. The maximum possible score on the SALT scale is limited to 100. However, there may be a pathophysiological mechanism in patients with AT/AU that is not adequately reflected in the SALT scale, which could drive the lower efficacy in the AT/AU group.

The CBO model-based simulation further informed the impact of treatment interruption on the loss of efficacy in the absence of a dedicated treatment withdrawal study. The results indicated that temporary treatment interruption for ≤ 6 weeks is not expected to result in a loss of SALT≤ 20 response in the majority of patients. However, treatment interruptions of a longer period may lead to significant loss of regrown scalp hair, as represented by almost 70% of SALT ≤ 20 responders losing SALT ≤ 20 response by 48 weeks after treatment withdrawal. Given challenges in a formal randomized treatment withdrawal study due to patients’ psychological burden with new hair loss, the model-based simulation was considered as an alternative approach to provide a quantitative assessment of the impact of treatment interruption on treatment outcome.

5 Conclusion

The longitudinal ER relationship of ritlecitinib was successfully characterized using a CBO modeling approach. The developed CBO model was utilized to contextualize phase 3 study findings, support the single pivotal trial strategy, and guide dose selection in the ritlecitinib program. The concept of CBO modeling based on raw score and subsequent simulations can be applied to any indication where efficacy is measured on a bounded scale to facilitate decision making in the accelerated drug development paradigm.

Clinical Trial Registration Numbers NCT02974868, NCT03732807, and NCT04006457.