Statistical inference for discretely sampled stochastic functional differential equations with small noise

Abstract

Estimating parameters of drift and diffusion coefficients for multidimensional stochastic delay equations with small noise are considered. The delay structure is written as an integral form with respect to a delay measure. Our contrast function is based on a local-Gauss approximation to the transition probability density of the process. We show consistency and asymptotic normality of the minimum-contrast estimator when a small dispersion coefficient $\varepsilon \rightarrow 0$ and sample size $n\rightarrow \infty$ simultaneously.

1 Introduction

Let $(\Omega ,{\mathscr {F}},\{{\mathscr {F}}_t\},P)$ be a stochastic basis satisfying the usual conditions. We consider a family of d-dimensional stochastic functional differential equations (SFDEs): for $\varepsilon \in (0,1]$ and $\delta >0$,

$$\begin{aligned} \left\{ \begin{array}{l} \textrm{d}X_t^\varepsilon =b\big (X_t^\varepsilon ,H(X_{t-\cdot }^\varepsilon ),\theta _0\big )\,\textrm{d}t+\varepsilon \sigma \big (X_t^\varepsilon ,H(X_{t-\cdot }^\varepsilon ),\beta _0\big )\,\textrm{d}W_t, \quad t\in [0,1];\\ X_t^\varepsilon =\phi ^\varepsilon (t), \quad t\in [-\delta , 0); \\ X_0^\varepsilon =\phi ^\varepsilon (0)=x_0^\varepsilon ,{\quad x_0\in {\mathbb {R}}^d;} \end{array} \right. \end{aligned}$$

(1.1)

where $\theta _0=(\alpha _0,\beta _0)\in \mathring{\Theta }$ with $\Theta =\overline{\Theta }_{\alpha }\times \overline{\Theta }_{\beta }$ for open bounded convex subsets $\Theta _{\alpha }$ and $\Theta _{\beta }$ of ${\mathbb {R}}^p$ and ${\mathbb {R}}^q$, respectively; $b=(b_1,\dots ,b_d):{\mathbb {R}}^d\times {\mathbb {R}}^d\times \Theta \rightarrow {\mathbb {R}}^d$ and $\sigma =(\sigma _{ij})_{d\times r}:{\mathbb {R}}^d\times {\mathbb {R}}^d\times \overline{\Theta }_{\beta }\rightarrow {\mathbb {R}}^{d}\otimes {\mathbb {R}}^r$ are known functions; $W_t=(W_t^1, \dots , W_t^r)$ is an r-dimensional Wiener process. Moreover, $\phi ^\varepsilon (t)$ is an ${\mathscr {F}}_0$ measurable ${\mathbb {R}}^d$-valued random variable for each $t \in [-\delta ,0]$ and $\varepsilon \in (0,1]$. Letting C(A; B) be the space of continuous functions from A to B, we also define a functional $H:C([0,\delta ];{\mathbb {R}}^d)\rightarrow {\mathbb {R}}^d$ as follows: for a continuous function $F_{t-\cdot }: u\mapsto F_{t-u}$ in $u\in [0,\delta ]$,

$$\begin{aligned} H(F_{t-\cdot })=\int _0^{\delta }F_{t-u}\,\mu (\textrm{d}u), \end{aligned}$$

where $\mu$ is a finite measure on $[0,\delta ]$. We call the Eq. (1.1) stochastic functional delay equations (SFDEs) since the functional H provides a delay structure in the SDE. Especially, when the measure $\mu$ is a Dirac measure, the SDE is just called a stochastic delay differential equation (SDDE).

We assume that the process $\{X_t^\varepsilon \}$ is observed at regularly spaced time points $\{t_k=k/n\,|\,k=0,\dots ,n\}\cup \{-i/n\,|\,i=1,\dots ,\lfloor n\delta \rfloor \}$ with the floor function $\lfloor \cdot \rfloor$. Our goal is to construct an estimator of $\theta _0$ from discrete observations $\{X_{t_k}^\varepsilon \}\cup \{X_{-i/n}^\varepsilon \}$, and to investigate the asymptotic behavior when $\varepsilon \rightarrow 0$ as well as $n\rightarrow \infty$.

There are many applications of (deterministic) delay differential equations (DDEs) in biology, epidemiology, physics, finance and insurance. For example, Mackey and Glass (1977) consider a homogeneous population of mature circulating cells (white blood cell, red blood cell, or platelet). Hu and Wang (2002) take account of the dynamics of controlled mechanical systems, among others. Due to those, their corresponding stochastic versions (SDDEs) of those differential equations also has been well investigated. Volterra (1959) considers predator–prey models; Guttrop and Kulperger (1984) take the effect of random elements into account, and they change Volterra’s model from DDEs to SDDEs; Fu (2019) considers a stochastic SIR model with delay for an epidemic model, and also, De la Sen and Ibeas (2021) consider SE(Is)(Ih)AR model as a COVID-19 model. From a theoretical point of view, Mohammed (1984), and Arriojas (1997) have generalized those models to SFDEs. Furthermore, the delay structure can appear in finance and insurance applications, e.g., Wang (2023) and their references, where the drift coefficient can include the diffusion parameter $\beta$; e.g., Example 1 in Wang (2023). Therefore our general setting in SFDE (1.1), where $\theta$ includes $\beta$ makes sense in applications.

Turnning our attention to statistical inference for SDDEs and SFDEs, there have been many works so far. Gushchin and Küchler (1999) and Küchler and Kutoyants (2000) study the asymptotic behavior of the maximum likelihood type estimators; Küchler and Sørensen (2013) consider the pseudo-likelihood estimator for SDDEs; Küchler and Vasiliev (2005) propose a sequential procedure with a given accuracy in the $L_2$ sense. Moreover, Reiss (2004, 2005) investigate nonparametric inference for affine SDDEs; Ren and Wu (2019) consider least squares estimates for path-dependent McKean-Vlasov SDEs from discrete observations.

Although all of those are studied in the ergodic context, we are interested in the small noise case, $\epsilon \rightarrow 0$, which is useful to justify the validity of the estimators since, in most applications of SFDEs, the ergodicity is often not expected. There are several initiative works by Kutoyants (1988, 1994) as for the small nose SFDEs from continuous observations, and the statistical problem should be separated according to parameters. For example, the parameters $\theta$ in (1.1) can usually be regular, but if the delay functional H includes unknown parameters, which are non-regular, the estimation problem becomes non-standard; see Kutoyants (1988). Therefore, we consider the former case only and suppose that the functional H is known in this paper.

In this paper, we consider a local-Gauss type contrast function and show the asymptotic normality of the minimum contrast estimators.

The paper is organized as follows. In Sect. 2, we make notation and assumptions and state our main results in Sect. 3. In Sect. 4, we provide some numerical studies to support our results. All the mathematical proofs are put in Sect. 5.

2 Notation and assumptions

2.1 Notation

• (N1) $X_t^0$ is the solution of the ordinary differential equations under the true value of the drift parameter for $t\in [0,1]$: $X_0^0=\phi (0)=x_0$ and

  $$\begin{aligned} \left\{ \begin{array}{ll} \textrm{d}X_t^0 = b\left( X_t^0,H(X_{t-\cdot }^0),\theta _0\right) \,\textrm{d}t, &{} t\in [0,1];\\ X_t^0 = \phi (t), &{} t\in [-\delta ,0), \end{array} \right. \end{aligned}$$

  where $\phi \in C([-\delta , 0];{\mathbb {R}}^d)$ and $x_0$ is constant. As for the existence and uniqueness of the solution, see the proof of Theorem 3.7 and Remark 3.8 by Smith (2011).

• (N2) For matrix A, the (i, j)th element is written by $A^{ij}$, and that

  $$\begin{aligned} |A|^2=\textrm{tr}\left( AA^\top \right) , \end{aligned}$$

  where $A^\top$ is the transpose of A and $\textrm{tr}\left( AA^\top \right)$ is the trace of $AA^\top$.

• (N3) For multi-index $m=(m_1,\dots ,m_k)$, a derivative operator in $z\in {\mathbb {R}}^k$ is given by

  $$\begin{aligned} \partial _z^m:=\partial _{z_1}^{m_1}\cdots \partial _{z_k}^{m_k},\qquad \partial _{z_i}^{m_i}:=\left( \partial /\partial _{z_i}\right) ^{m_i}. \end{aligned}$$

• (N4) Let $C^{j,k,l}({\mathbb {R}}^d\times {\mathbb {R}}^d\times \Theta ;{\mathbb {R}}^N)$ be the space of all functions f satisfying that $f(x,y,\theta )$ is a ${\mathbb {R}}^N$-valued function on ${\mathbb {R}}^d\times {\mathbb {R}}^d\times \Theta$ which j, k and l times continuously differentiable with respect to x, y and $\theta$, respectively.

• (N5) $C_{\uparrow }^{j,k,l}({\mathbb {R}}^d\times {\mathbb {R}}^d\times \Theta ;{\mathbb {R}}^N)$ is a class of $C^{j,k,l}({\mathbb {R}}^d\times {\mathbb {R}}^d\times \Theta ;{\mathbb {R}}^N)$ satisfying that

  $$\begin{aligned} \sup _{\theta \in \Theta }|\partial ^\mu _\theta \partial ^\nu _y\partial ^\xi _x f(x,y,\theta )|\le C(1+|x|+|y|)^\lambda , \end{aligned}$$

  for universal positive constants C and $\lambda$, where for $M=\textrm{dim}(\Theta )$, $\mu =(\mu _1,\dots ,\mu _M)$, $\nu =(\nu _1,\dots ,\nu _d)$ and $\xi =(\xi _1,\dots ,\xi _d)$ are multi-indices with $0\le \sum _{i=1}^M\mu _i\le l$, $0\le \sum _{i=1}^d\nu _i\le k$ and $0\le \sum _{i=1}^d\xi _i\le j$, respectively.

• (N6) Denote by $G({{\gamma }})$ the set of all permutations on $\{1,\dots ,{{\gamma }}\}$.

• (N7) For elements $\left\{ b^i\right\}$ and $\left\{ [\sigma \sigma ^\top ]^{ij}\right\}$, we denote by

  $$\begin{aligned} b^i_{t,H}(\theta ):=b^i\left( X_t^\varepsilon ,H\left( X_{t-\cdot }^\varepsilon \right) ,\theta \right) ,\quad [\sigma \sigma ^\top ]_{t,H}^{ij}(\beta ):=[\sigma \sigma ^\top ]^{ij}\left( X_t^\varepsilon ,H\left( X_{t-\cdot }^\varepsilon \right) ,\beta \right) . \end{aligned}$$

• (N8) Denote by $\Delta _kX^\varepsilon := X_{t_k}^\varepsilon -X_{t_{k-1}}^\varepsilon$ and

  $$\begin{aligned} B\left( X_t^0, \theta _0, \theta \right) := b\left( X_t^0,H\left( X_{t-\cdot }^0\right) ,\theta _0\right) -b\left( X_t^0,H\left( X_{t-\cdot }^0\right) ,\theta \right) . \end{aligned}$$

2.2 Assumptions

We make the following assumptions:

• (A1) There exists a constant $K>0$ such that

  $$\begin{aligned} |b(x,y,\theta )-b({\tilde{x}},{\tilde{y}},\theta )|+|\sigma (x,y,{\beta })-\sigma ({\tilde{x}},{\tilde{y}},{\beta })|&\le K\left( |x-{\tilde{x}}|+|y-{\tilde{y}}|\right) ,\\ |b(x,y,\theta )|+|\sigma (x,y,{\beta })|&\le K\left( 1+|x|+|y|\right) , \end{aligned}$$

  for each $x,{\tilde{x}},y,{\tilde{y}}\in {\mathbb {R}}^d$, $\theta \in \Theta$ and $\beta \in \overline{\Theta }_{\beta }$.

• (A2) For any ${{\gamma }}\ge 1$,

  $$\begin{aligned} \sup _{\varepsilon \in (0,1]}E\left[ \sup _{t\in [-\delta ,0]}|\phi ^\varepsilon (t)|^{{\gamma }} \right] <\infty , \end{aligned}$$

  and there exists a constant $K_1,K_2>0$ such that

  $$\begin{aligned} E\left[ |\phi ^\varepsilon (t)-\phi ^\varepsilon (s)|^{{\gamma }} \right] \le K_1|t-s|^{{\gamma }} + K_2\varepsilon ^{{\gamma }} |t-s|^{{{\gamma }}/2}. \end{aligned}$$

  Moreover, as $\varepsilon \rightarrow 0$,

  $$\begin{aligned} E\left[ \sup _{-\delta \le t\le 0}|\phi ^{\varepsilon }(t)-\phi (t)|^{{\gamma }} \right] =O(\varepsilon ^{{\gamma }} ). \end{aligned}$$

• (A3) $b\left( \cdot ,\cdot ,\cdot \right) \in C_{\uparrow }^{2,1,3}\left( {\mathbb {R}}^d\times {\mathbb {R}}^d\times \Theta ;{\mathbb {R}}^d\right)$, $\sigma (\cdot ,\cdot ,\cdot )\in C_{\uparrow }^{2,1,3}\left( {\mathbb {R}}^d\times {\mathbb {R}}^d\times \overline{\Theta }_{\beta };{\mathbb {R}}^d\otimes {\mathbb {R}}^r\right)$.

• (A4) The matrix $[\sigma \sigma ^\top ]\left( x,y,\beta \right)$ is positive definite for each $x,y\in {\mathbb {R}}^d$ and $\beta \in \overline{\Theta }_{\beta }$, and that

  $$\begin{aligned} \inf _{x,y\in {\mathbb {R}}^d,\beta \in \overline{\Theta }_{\beta }}\det [\sigma \sigma ^\top ]\left( x,y,\beta \right) >0. \end{aligned}$$

  Moreover, $[\sigma \sigma ^\top ]^{-1}(\cdot ,\cdot ,\cdot )\in C_{\uparrow }^{1,1,3}\left( {\mathbb {R}}^d\times {\mathbb {R}}^d\times \overline{\Theta }_{\beta };{\mathbb {R}}^d\otimes {\mathbb {R}}^d\right)$.

• (A5) If $\theta \ne \theta _0$ then $b(X_t^0,H(X_{t-\cdot }^0),\theta )\ne b(X_t^0,H(X_{t-\cdot }^0),\theta _0)$; If $\beta \ne \beta _0$ then $[\sigma \sigma ^\top ](X_t^0,H(X_{t-\cdot }^0),\beta )\ne [\sigma \sigma ^\top ](X_t^0,H(X_{t-\cdot }^0),\beta _0)$, for at least one value of t, respectively.

• (A6) The matrix

  $$\begin{aligned} I(\theta _0)= \left( \begin{array}{cc} \left( I_b^{ij}(\theta _0)\right) _{1\le i,j\le p} &{} 0\\ 0 &{} \left( I_\sigma ^{ij}(\theta _0)\right) _{1\le i,j\le q}\\ \end{array} \right) , \end{aligned}$$

  is positive definite, where

  $$\begin{aligned} I_b^{ij}(\theta _0)&=\int _0^1\bigg (\frac{\partial }{\partial \alpha _i}b\left( X_{s}^0,H\left( X_{s-\cdot }^0\right) ,\theta _0\right) \bigg )^{\top }[\sigma \sigma ^\top ]^{-1}\left( X_s^0,H\left( X_{s-\cdot }^0\right) ,\beta _0\right) \\&\quad \bigg (\frac{\partial }{\partial \alpha _j}b\left( X_{s}^0,H\left( X_{s-\cdot }^0\right) ,\theta _0\right) \bigg )\,\textrm{d}s,\\ I_\sigma ^{ij}(\theta _0)&=\frac{1}{2}\int _0^1\textrm{tr}\Bigg [\bigg (\frac{\partial }{\partial \beta _i}[\sigma \sigma ^{\top }]\bigg )[\sigma \sigma ^\top ]^{-1}\bigg (\frac{\partial }{\partial \beta _j} [\sigma \sigma ^\top ]\bigg )[\sigma \sigma ^\top ]^{-1}\left( X_s^0,H\left( X_{s-\cdot }^0\right) ,\beta _0\right) \Bigg ]\,\textrm{d}s. \end{aligned}$$

Remark 1

Although the assumption (A4) seems a bit restrictive, it is the same assumption as [A3’] in Gloter and Sørensen (2009).

3 Main theorems

For estimation of $\theta \in \Theta$ in (1.1), we consider the following local-Gauss type contrast function:

$$\begin{aligned} U_{n,\varepsilon }(\theta )=\sum _{k=1}^{n}\left\{ \log \det \Xi _{k-1}(\beta )+\frac{n}{\varepsilon ^2}P_k^\top (\theta )\Xi _{k-1}^{-1}(\beta )P_k(\theta )\right\} , \end{aligned}$$

where

$$\begin{aligned} P_k(\theta )=\Delta _k X^{{\epsilon }}-\frac{1}{n}b\left( X_{t_{k-1}}^{{\epsilon }},H_n(X_{t_{k-1}-\cdot }^{{\epsilon }}), \theta \right) ,\quad \Xi _{k-1}(\beta )=[\sigma \sigma ^{\top }]\left( X_{t_{k-1}}^{{\epsilon }}, H_n(X_{t_{k-1}-\cdot }^{{\epsilon }}),\beta \right) , \\ H_n(X_{t_{k-1}-\cdot }^{{\epsilon }})=\sum _{i=1}^{\lfloor n\delta \rfloor }\left\{ X_{t_{k-1}-(i-1)/n}^{{\epsilon }}~\mu \big ([(i-1)/n, i/n{]}\big )\right\} +X_{t_{k-1}-\delta _n}^{{\epsilon }}~\mu \big ([\delta _n, \delta ]\big ), \end{aligned}$$

and $\delta _n:= \lfloor n\delta \rfloor /n$.

Definition 1

A minimum contrast estimator $\widehat{\theta }_{n,\varepsilon }=(\widehat{\alpha }_{n,\varepsilon },\widehat{\beta }_{n,\varepsilon })$ is defined as

$$\begin{aligned} U_{n,\varepsilon }(\widehat{\theta }_{n,\varepsilon })=\inf _{\theta \in \Theta }U_{n,\varepsilon }(\theta ). \end{aligned}$$

The consistency of our estimator $\widehat{\theta }_{n,\varepsilon }$ is given as follows.

Theorem 1

Suppose the assumptions (A1)–(A5). Then we have

$$\begin{aligned} \widehat{\theta }_{n,\varepsilon } \xrightarrow {P}\theta _0, \end{aligned}$$

if $(\sqrt{n}\varepsilon )^{-1}\rightarrow 0$ as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$.

The next theorem gives the asymptotic normal distribution of $\widehat{\theta }_{n,\varepsilon }$.

Theorem 2

Suppose the assumptions (A1)–(A6). Then we have

$$\begin{aligned} \left( \begin{array}{rr} \varepsilon ^{-1}(\widehat{\alpha }_{n,\varepsilon }-\alpha _0) \\ \sqrt{n}(\widehat{\beta }_{n,\varepsilon }-\beta _0) \\ \end{array} \right) \xrightarrow {d} N\left( 0,I^{-1}(\theta _0)\right) , \end{aligned}$$

if $(\sqrt{n}\varepsilon )^{-1}\rightarrow 0$ as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$.

4 Simulations

We consider the following 2 -dimensional SFDE:

$$\begin{aligned} \left\{ \begin{aligned} \textrm{d}X_t^{(1)}=\alpha _1H(X_{t-\cdot }^{(2)})\,\textrm{d}t+\varepsilon \beta _1\sqrt{1+\left( H(X_{t-\cdot }^{(2)})\right) ^2}\,\textrm{d}W_t^1,\\ \textrm{d}X_t^{(2)}=\alpha _2H(X_{t-\cdot }^{(1)})\,\textrm{d}t+\varepsilon \beta _2\sqrt{1+\left( H(X_{t-\cdot }^{(1)})\right) ^2}\,\textrm{d}W_t^2, \end{aligned} \right. \end{aligned}$$

for $t\in [0,1]$,

$$\begin{aligned} \left\{ \begin{aligned} \textrm{d}X_t^{(1)}=5X_t^{(2)}\,\textrm{d}t+7\varepsilon \sqrt{1+\left( X_t^{(2)}\right) ^2}\,\textrm{d}W_t^1,\\ \textrm{d}X_t^{(2)}=6X_t^{(1)}\,\textrm{d}t+8\varepsilon \sqrt{1+\left( X_t^{(1)}\right) ^2}\,\textrm{d}W_t^2, \end{aligned} \right. \end{aligned}$$

for $t\in [-\delta ,0]$, where $\delta =1/10$, $\left( X_{-\delta }^{(1)},X_{-\delta }^{(2)}\right) =(1,2)$ and $H(X_{t-\cdot })=X_{t-\delta }$. In this example, the estimator is given explicitly as follows:

$$\begin{aligned} \widehat{\theta }_{n,\varepsilon }=(\widehat{\alpha }_{n,\varepsilon },\widehat{\beta }_{n,\varepsilon }) =(\widehat{\alpha }_{n,\varepsilon ,1},\widehat{\alpha }_{n,\varepsilon ,2},\widehat{\beta }_{n,\varepsilon ,1}, \widehat{\beta }_{n,\varepsilon ,2}), \end{aligned}$$

where

$$\begin{aligned} \widehat{\alpha }_{n,\varepsilon ,1}= & {} \frac{n\displaystyle \sum _{k=1}^{n}\frac{H_n(X_{t_{k-1}-\cdot }^{(2)})}{1+\left( H_n(X_{t_{k-1}-\cdot }^{(2)})\right) ^2}}{\displaystyle \sum _{k=1}^{n} \frac{\left( H_n(X_{t_{k-1}-\cdot }^{(2)})\right) ^2}{1+\left( H_n(X_{t_{k-1}-\cdot }^{(2)})\right) ^2}}, \quad \widehat{\alpha }_{n,\varepsilon ,2} = \frac{n\displaystyle \sum _{k=1}^{n}\frac{H_n(X_{t_{k-1}-\cdot }^{(1)})}{1+\left( H_n(X_{t_{k-1}-\cdot }^{(1)})\right) ^2}}{\displaystyle \sum _{k=1}^{n} \frac{\left( H_n(X_{t_{k-1}-\cdot }^{(1)})\right) ^2}{1+\left( H_n(X_{t_{k-1}-\cdot }^{(1)})\right) ^2}}, \\ \widehat{\beta }_{n,\varepsilon ,1}= & {} \varepsilon ^{-1}\displaystyle \sqrt{\sum _{k=1}^{n}\frac{\left( \Delta _{t_{k-1}}X^{(1)} -\frac{\widehat{\alpha }_{n,\varepsilon ,1}}{n}H_n(X_{t_{k-1}-\cdot }^{(2)})\right) ^2}{1+\left( H_n(X_{t_{k-1}-\cdot }^{(2)})\right) ^2}}, \\ \widehat{\beta }_{n,\varepsilon ,2}= & {} \varepsilon ^{-1}\displaystyle \sqrt{\sum _{k=1}^{n}\frac{\left( \Delta _{t_{k-1}}X^{(2)} -\frac{\widehat{\alpha }_{n,\varepsilon ,1}}{n}H_n(X_{t_{k-1}-\cdot }^{(1)})\right) ^2}{1+\left( H_n(X_{t_{k-1}-\cdot }^{(1)})\right) ^2}}, \end{aligned}$$

and $H_n(X_{t-\cdot })=X_{t-\delta _n}$.

In the experiments, we generate discrete samples $\{X_{t_{k}}\}_{k=1}^n$ and $\{X_{-i/n}\}_{i=1}^{n\delta _n}$ by the Euler-Maruyama method (see Backwar (2006)). We show means and standard deviations of estimators through 1000 times replications according to several values of $(n,\varepsilon )$ in Tables 1, 2 and 3, which illustrate the consistency of our estimator.

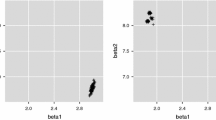
We also show the results of normal Q-Q plot in the ideal case where $(n,\varepsilon ) = (10000, 0.01)$ in Figs. 1, 2, 3 and 4, which illustrate the asymptotic normality of each marginal of $\widehat{\theta }_{n,\varepsilon }$. Moreover, Fig. 5 shows that the distribution of the bilinear form of the estimator follows the $\chi ^2(4)$-distribution, which illustrates the (joint) asymptotic normality of $\widehat{\theta }_{n,\varepsilon }$.

Table 1 Mean and standard deviation of the estimator $\widehat{\theta }_{n,\varepsilon }$ through 1000 experiments as $\varepsilon =0.1$

Table 2 Mean and standard deviation of the estimator $\widehat{\theta }_{n,\varepsilon }$ through 1000 experiments as $\varepsilon =0.03$

Table 3 Mean and standard deviation of the estimator $\widehat{\theta }_{n,\varepsilon }$ through 1000 experiments as $\varepsilon =0.01$

Fig. 1

Normal Q-Q plot as $\theta =(1.0, 2.0, 3.0, 4.0), \varepsilon =0.01, n=10,000$ for 1000 iterated samples of $\varepsilon ^{-1}\sqrt{I_{b}^{11}(\theta _0)}(\widehat{\alpha }_{n,\varepsilon ,1}-\alpha _1)$

Fig. 2

Normal Q-Q plot as $\theta =(1.0, 2.0, 3.0, 4.0), \varepsilon =0.01, n=10,000$ for 1000 iterated samples of $\varepsilon ^{-1}\sqrt{I_{b}^{22}(\theta _0)}(\widehat{\alpha }_{n,\varepsilon ,2}-\alpha _2)$

Fig. 3

Normal Q-Q plot as $\theta =(1.0, 2.0, 3.0, 4.0), \varepsilon =0.01, n=10,000$ for 1000 iterated samples of $\sqrt{n}\sqrt{I_{\sigma }^{11}(\theta _0)}(\widehat{\beta }_{n,\varepsilon ,1}-\beta _1)$

Fig. 4

Normal Q-Q plot as $\theta =(1.0, 2.0, 3.0, 4.0), \varepsilon =0.01, n=10,000$ for 1000 iterated samples of $\sqrt{n}\sqrt{I_{\sigma }^{22}(\theta _0)}(\widehat{\beta }_{n,\varepsilon ,2}-\beta _2)$

Fig. 5

Chi square(4) Q-Q plot as $\theta =(1.0, 2.0, 3.0, 4.0), \varepsilon =0.01, n=10,000$ for 1000 iterated samples of $\big (\varepsilon ^{-1}(\widehat{\alpha }_{n,\varepsilon }-\alpha ), \sqrt{n}(\widehat{\beta }_{n,\varepsilon ,}-\beta )\big )^{\top }I(\theta _0)\big (\varepsilon ^{-1}(\widehat{\alpha }_{n,\varepsilon }-\alpha ), \sqrt{n}(\widehat{\beta }_{n,\varepsilon ,}-\beta )\big )$

5 Proofs

We first establish some preliminary lemmas. The idea of the proof of Lemma 1 is due to that of Lemma 2.2.1 by Nualart (2006).

First, we will give a result for the existence of a strong solution for (1.1). Although different conditions for more general types of diffusions are seen in, e.g., Liptser and Shiryayev (2001), Theorem 4.6, we will concentrate on a more specific case, where the conditions become simpler for practical use.

Lemma 1

Suppose that (A1) and (A2) hold true. Then there exists a strong solution $\left\{ X_t^\varepsilon \right\}$ for $\varepsilon \in (0,1]$. Moreover, for ${{\gamma }}\ge 2$, it holds true:

$$\begin{aligned} E\left[ \sup _{-\delta \le t\le 1}\left| X_t^\varepsilon \right| ^{{\gamma }} \right] <\infty . \end{aligned}$$

Proof

Let

$$\begin{aligned} X_t^0= {\left\{ \begin{array}{ll} x_0,\quad t\in [0,1];\\ \phi ^\varepsilon (t),\quad t\in [-\delta ,0); \end{array}\right. } \end{aligned}$$

and for $n\ge 0$,

$$\begin{aligned} X_t^{n+1}= {\left\{ \begin{array}{ll} x_0^\varepsilon +\int _{0}^{t}b\left( X_s^n,H(X_{s-\cdot }^n),\theta _0\right) \,\textrm{d}s+\varepsilon \int _0^t\sigma \left( X_s^n,H(X_{s-\cdot }^n),\beta _0\right) \,\textrm{d}W_s,\quad t\in [0,1];\\ \phi ^\varepsilon (t),\quad t\in [-\delta ,0]. \end{array}\right. } \end{aligned}$$

First, we show that there exists a strong solution $\left\{ X_t^\varepsilon \right\}$. From Lemma 2.2.1 of Nualart (2006), it suffices to show that

$$\begin{aligned} E\left[ \sup _{-\delta \le t\le 1}\left| X_t^{n}\right| ^{{\gamma }} \right] <\infty , \end{aligned}$$

(5.1)

and

$$\begin{aligned} \sum _{n=0}^{\infty }E\left[ \sup _{-\delta \le t\le 1}\left| X_{t}^{n+1}-X_{t}^{n}\right| ^{{\gamma }} \right] <\infty , \end{aligned}$$

(5.2)

for any ${{\gamma }}\ge 2$. By a recursive argument, we can show that the inequality (5.1) holds. By using the Burkholder-Davis-Gundy inequality and (A1),

$$\begin{aligned} E\left[ \sup _{-\delta \le t\le 1}\left| X_t^{n+1}\right| ^{{\gamma }} \right]&\le E\left[ \sup _{-\delta \le t \le 0}\left| X_t^{n+1}\right| ^{{\gamma }} \right] +E\left[ \sup _{0\le t\le 1}\left| X_t^{n+1}\right| ^{{\gamma }} \right] \\&\le C_{{\gamma }}\Bigg \{E\left[ \sup _{-\delta \le t\le 0}\left| \phi ^\varepsilon (t)\right| ^{{\gamma }} \right] +E\left[ \left| x_0^\varepsilon \right| ^{{\gamma }} \right] +E\bigg [\int _0^1\Big |b\left( X_{s}^n,H(X_{s-\cdot }^n),\theta _0\right) \Big |^{{\gamma }} \,\textrm{d}s\bigg ]\\&\quad +\varepsilon ^{{\gamma }} E\Bigg [\bigg |\int _0^1\sigma \left( X_{s}^n,H(X_{s-\cdot }^n),\theta _0\right) \,\textrm{d}W_s\bigg |^{{\gamma }} \Bigg ]\Bigg \}\\&\le C_{{\gamma }}\Bigg \{E\left[ \sup _{-\delta \le t\le 0}\left| \phi ^\varepsilon (t)\right| ^{{\gamma }} \right] +E\left[ \big |x_0^\varepsilon \big |^{{\gamma }} \right] \\&\quad +K^{{\gamma }} C'_{{\gamma }}\int _0^1\left( 1+E\big [|X_s^n|^{{\gamma }} \big ]+\left( \mu \left( \left[ 0,\delta \right] \right) \right) ^{{\gamma }} E\left[ \sup _{0\le u\le \delta }\left| X_{s-u}^n\right| ^{{\gamma }} \right] \right) \,\textrm{d}s\Bigg \}\\&\le C_{{\gamma }}\Bigg \{E\left[ \sup _{-\delta \le t\le 0}\left| \phi ^\varepsilon (t)\right| ^{{\gamma }} \right] +E\left[ \big |x_0^\varepsilon \big |^{{\gamma }} \right] \\&\quad +K^{{\gamma }} C'_{{\gamma }}\left( 1+\sup _{0\le s\le 1}E\left[ |X_s^n|^{{\gamma }} \right] +\left( \mu \left( \left[ 0,\delta \right] \right) \right) ^{{\gamma }} \sup _{0\le s\le 1}E\left[ \sup _{0\le u\le \delta }\left| X_{s-u}^n\right| ^{{\gamma }} \right] \right) \Bigg \}\\&\le C_{{\gamma }}\Bigg \{E\left[ \sup _{-\delta \le t\le 0}\left| \phi ^\varepsilon (t)\right| ^{{\gamma }} \right] +E\left[ \big |x_0^\varepsilon \big |^{{\gamma }} \right] \\&\quad +K^{{\gamma }} C'_{{\gamma }}\left( 1+\sup _{0\le s\le 1}E\left[ \left| X_s^n\right| ^{{\gamma }} \right] +\left( \mu \left( \left[ 0,\delta \right] \right) \right) ^{{\gamma }} E\left[ \sup _{-\delta \le s\le 1}\left| X_{s}^n\right| ^{{\gamma }} \right] \right) \Bigg \}, \end{aligned}$$

where $C_{{\gamma }}$ and $C'_{{\gamma }}$ are constants depending only on ${{\gamma }}$. For (5.2), by applying the Burkholder-Davis-Gundy inequality and (A1) again, we have

$$\begin{aligned} E\left[ \sup _{-\delta \le t\le 1}\left| X_{t}^{n+1}-X_{t}^{n}\right| ^{{\gamma }} \right]&\le C_{{\gamma }}\left\{ 1+\left( \mu \left( \left[ 0,\delta \right] \right) \right) ^{{\gamma }} \right\} \int _0^1E\left[ \sup _{0\le u\le \delta }\left| X_{s-u}^n-X_{s-u}^{n-1}\right| ^{{\gamma }} \right] \,\textrm{d}s\\&\le \frac{1}{n!}\left[ C_{{\gamma }}\left\{ 1+\left( \mu \left( \left[ 0,\delta \right] \right) \right) ^{{\gamma }} \right\} \right] ^{n+1}E\left[ \sup _{-\delta \le t\le 1}|X_t^1|^{{\gamma }} \right] . \end{aligned}$$

Consequently, we have the inequality (5.2) by (5.1).

Finally, we shall prove that the solution of (1.1) is unique. We assume that ${\tilde{X}}_t^\varepsilon$ is the solution of (1.1). Then, it follows by (A1) that

$$\begin{aligned} E\left[ \sup _{-\delta \le u \le 0}\left| X_{t-u}^\varepsilon -{\tilde{X}}_{t-u}^\varepsilon \right| ^2\right] \le 8K^2\Bigg \{\int _0^tE\left[ \sup _{-\delta \le u \le 0}\left| X_{s-u}^\varepsilon -{\tilde{X}}_{s-u}^\varepsilon \right| ^2\right] \,\textrm{d}s\\ +\mu \left( \left[ 0,\delta \right] \right) \int _0^tE\left[ \sup _{-\delta \le u \le 0}\left| X_{s-u}^\varepsilon -{\tilde{X}}_{s-u}^\varepsilon \right| ^2\right] \,\textrm{d}s\Bigg \}. \end{aligned}$$

Hence, it follows from Gronwall’s inequality that

$$\begin{aligned} E\left[ \sup _{-\delta \le u \le 0}\left| X_{t-u}^\varepsilon -{\tilde{X}}_{t-u}^\varepsilon \right| ^2\right] =0. \end{aligned}$$

The proof is completed. $\square$

For Lemma 2, we shall use the notations:

• (N9) Denote by $Y_t^{n,\varepsilon }:=X_{\lfloor nt \rfloor /t}^\varepsilon$ and $Y_{t-\cdot }^{n,\varepsilon }:=X_{\lfloor nt \rfloor /t-\cdot }^\varepsilon$ for the stochastic process $X^\varepsilon$ defined by (1.1).

• (N10) For $X_{t-\cdot }^\varepsilon \in C\left( [0,\delta ];{\mathbb {R}}^d\right)$, denote by $\left\| X_{t-\cdot }^\varepsilon \right\| _\infty :=\sup _{0\le u \le \delta }\left| X_{t-u}^\varepsilon \right| .$

In Lemma 2, the proof ideas follow Long et al. (2013)

Lemma 2

Suppose that (A1) and (A2) hold true. Then, it follows for ${{\gamma }}\ge 1$,

$$\begin{aligned} E\left[ \sup _{0\le t\le 1}\left| Y_{t}^{n,\varepsilon }-X_{t}^{0}\right| ^{{\gamma }} \right]&=O\left( \varepsilon ^{{\gamma }} \right) +O\left( 1/n^{{\gamma }} \right) ; \\ E\left[ \sup _{0\le t\le 1}\left\| Y_{t-\cdot }^{n,\varepsilon }-X_{t-\cdot }^{0}\right\| _{\infty }^{{\gamma }} \right]&=O\left( \varepsilon ^{{\gamma }} \right) +O\left( 1/n^{{\gamma }} \right) \end{aligned}$$

as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$.

Proof

Since it is easy to see that

$$\begin{aligned} \left| Y_{t}^{n,\varepsilon }-X_t^0\right| ^{{\gamma }} \le \left\| Y_{t-\cdot }^{n,\varepsilon }-X_{t-\cdot }^0\right\| _{\infty }^{{\gamma }} \quad a.s., \end{aligned}$$

it suffices to show that $E\left[ \sup _{0\le t\le 1}\left\| Y_{t-\cdot }^{n,\varepsilon }-X_{t-\cdot }^{0}\right\| _{\infty }^{{\gamma }} \right] =O\left( \varepsilon ^{{\gamma }} \right) +O\left( 1/n^{{\gamma }} \right)$   as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$. We shall prove only the case where $\delta \ge 1$ because the proof for $\delta \le 1$ is almost the same. It follows from (A1) and the Burkholder-Davis-Gundy inequality that

$$\begin{aligned} E\left[ \sup _{0\le t\le 1}\left\| X_{t-\cdot }^\varepsilon -X_{t-\cdot }^{0}\right\| _{\infty }^{{\gamma }} \right]&\le E\left[ \sup _{0\le t\le 1}\sup _{0\le s\le t}\big \Vert X_{t-\cdot }^\varepsilon -X_{t-\cdot }^{0}\big \Vert _{\infty }^{{\gamma }} \right] \\&\quad +E\left[ \sup _{0\le t\le 1}\sup _{t\le s\le \delta }\big \Vert X_{t-\cdot }^\varepsilon -X_{t-\cdot }^{0}\big \Vert _\infty ^{{\gamma }} \right] \\&\le 2^{{\gamma }} E\Biggl [\sup _{0\le t \le 1}\bigg |\int _{0}^{t}b\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\theta _{0}\big )-b\big (X_{s}^{0},H(X_{s-\cdot }^0),\theta _{0}\big )\,\textrm{d}s\bigg |^{{\gamma }} \Biggr ]\\&\quad +2^{{\gamma }} \varepsilon ^{{\gamma }} E\Biggl [\sup _{0\le t \le 1}\bigg |\int _{0}^{t}\sigma \big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _{0}\big )\,\textrm{d}W_s\bigg |^{{\gamma }} \Biggr ]\\&\quad +E\left[ \sup _{0\le t\le 1}\sup _{t\le s\le \delta }\bigl |\phi ^\varepsilon (t-s)-\phi (t-s)\bigr |^{{\gamma }} \right] \\&\le 2^{{\gamma }} K^{{\gamma }} E\left[ \sup _{0\le t \le 1}\int _{0}^{t}\big |X_{s}^\varepsilon -X_{s}^{0}\big |^{{\gamma }} +\big |H(X_{s-\cdot }^\varepsilon )-H(X_{s-\cdot }^0)\big |^{{\gamma }} \,\textrm{d}s\right] \\&\quad +\varepsilon ^{{\gamma }} C_{{\gamma }} E\left[ \int _0^1\Big |\sigma _{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _{0}\big )\Big |^{{{\gamma }}/2}\,\textrm{d}s\right] \\&\quad +E\left[ \sup _{-\delta \le t\le 0}\bigl |\phi ^\varepsilon (t)-\phi (t)\bigr |^{{\gamma }} \right] \\&\le 2^{{\gamma }} K^{{\gamma }} \left( 1+\mu \left( [0,\delta ]\right) ^{{\gamma }} \right) E\left[ \int _{0}^{1}\sup _{0\le v\le s}\Vert X_{v-\cdot }^\varepsilon -X_{v-\cdot }^0\big \Vert _\infty ^{{\gamma }} \,\textrm{d}s\right] \\&\quad + \varepsilon ^{{\gamma }} C_{{\gamma }}\Big (1+E\left[ \sup _{0\le s \le 1}\big |X_{s}^{{\varepsilon }}\big |^{{{\gamma }}/2}\right] +\mu ([0,\delta ])^{{{\gamma }}/2}E\left[ \sup _{0\le s \le 1}\big \Vert X_{s-\cdot }^0\big \Vert _{\infty }^{{{\gamma }}/2}\right] \Big )\\&\quad +E\left[ \sup _{-\delta \le t\le 0}\bigl |\phi ^\varepsilon (t)-\phi (t)\bigr |^{{\gamma }} \right] , \end{aligned}$$

where $C_{{\gamma }}$ is a constant depending only on p. It holds from Gronwall’s inequality and (A2) that

$$\begin{aligned} E\left[ \sup _{0\le t\le 1}\left\| X_{t-\cdot }^\varepsilon -X_{t-\cdot }^{0}\right\| _{\infty }^{{\gamma }} \right]&\le \Biggl \{ \varepsilon ^{{\gamma }} C_{{\gamma }}\bigg (1+E\left[ \sup _{0\le s \le 1}\big |X_{s}^{{\varepsilon }}\big |^{{{\gamma }}/2}\right] +\mu ([0,\delta ])^{{{\gamma }}/2}E\left[ \sup _{0\le s \le 1}\big \Vert X_{s-\cdot }^0\big \Vert _{\infty }^{{{\gamma }}/2}\right] \bigg )\\&\quad +E\left[ \sup _{-\delta \le t\le 0}\bigl |\phi ^\varepsilon (t)-\phi (t)\bigr |^{{\gamma }} \right] \Biggr \} e^{2^{{\gamma }} K^{{\gamma }} \left( 1+\mu \left( [0,\delta ]\right) ^{{\gamma }} \right) }\\&=O(\varepsilon ^{{\gamma }} ), \end{aligned}$$

as $\varepsilon \rightarrow 0$. From the continuity of $X_t^0$, the proof is completed. $\square$

Remark 2

It is satisfied from the proof of Lemma 2 and (A2) that $\sup _{\varepsilon \in (0,1]} E\left[ \sup _{-\delta \le t\le 1}\left| X_t^\varepsilon \right| ^{{\gamma }} \right] <\infty$ for ${{\gamma }}\ge 1$.

Lemma 3

Suppose the conditions (A1) and (A2). Then the following (i) and (ii) hold as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$: for any ${{\gamma }}\ge 1$,

• (i) $\displaystyle E\left[ \sup _{t\in [0,1]}\left| H\left( Y_{t-\cdot }^{n,\varepsilon }\right) -H\left( X_{t-\cdot }^0\right) \right| ^{{\gamma }} \right] =O\left( \varepsilon ^{{\gamma }} \right) +O\left( 1/n^{{\gamma }} \right) .$

• (ii) $\displaystyle E\left[ \sup _{t\in [0,1]}\left| H_n\left( Y_{t-\cdot }^{n,\varepsilon }\right) -H\left( X_{t-\cdot }^0\right) \right| ^{{\gamma }} \right] =O\left( \varepsilon ^{{\gamma }} \right) +O\left( 1/n^{{\gamma }} \right) .$

Proof

• (i) From Lemma 2,

  $$\begin{aligned} E\left[ \sup _{t\in [0,1]}\left| H\left( Y_{t-\cdot }^{n,\varepsilon }\right) -H\left( X_{t-\cdot }^0\right) \right| ^{{\gamma }} \right]&\le \mu \left( [0,\delta ]\right) E\left[ \sup _{t\in [0,1]}\left\| Y_{t-\cdot }^{n,\varepsilon }-X_{t-\cdot }^{0}\right\| _{\infty }^{{\gamma }} \right] \\&= O\left( \varepsilon ^{{\gamma }} \right) +O\left( 1/n^{{\gamma }} \right) , \end{aligned}$$

  as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$.

• (ii) From Lemma 2 and the continuity of $X^0_t$, we have

  $$\begin{aligned} E\left[ \sup _{t\in [0,1]}\left| H_n\left( Y_{t-\cdot }^{n,\epsilon }\right) -H\left( X_{t-\cdot }^0\right) \right| ^{{{\gamma }}}\right]&\le \int _{0}^{\delta }E\left[ \sup _{t\in [0,1]}\left| Y_{t-\lfloor ns \rfloor /n}^{n,\epsilon }-X_{t-s}^0\right| ^{{{\gamma }}}\right] \,\mu (\textrm{d}s)\\&\le 2^{{{\gamma }}-1}\int _{0}^{\delta }\Bigg \{E\left[ \sup _{t\in [0,1]}\left| Y_{t-\lfloor ns \rfloor /n}^{n,\epsilon }-X_{\lfloor nt \rfloor /n-\lfloor ns \rfloor /n}^0\right| ^{{\gamma }} \right] \\&\quad +E\left[ \sup _{t\in [0,1]}\left| X_{\lfloor nt \rfloor /n-\lfloor ns \rfloor /n}^0-X_{t-s}^0\right| ^{{\gamma }} \right] \Bigg \}\,\mu (\textrm{d}s)\\&= O\left( \epsilon ^{{\gamma }} \right) +O\left( 1/n^{{\gamma }} \right) , \end{aligned}$$

  as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$.

$\square$

Lemma 4

Suppose the conditions (A1) and (A2). Then, it holds that

$$\begin{aligned} E\left[ \left| H(X_{t-\cdot }^{{\varepsilon }})-H_n(X_{t-\cdot }^{{\varepsilon }})\right| ^{{\gamma }} \right] =O\left( n^{-{{\gamma }}}\right) +O\left( \varepsilon ^{{\gamma }} n^{-{{\gamma }}/2}\right) , \end{aligned}$$

for ${{\gamma }}\ge 1$.

Proof

From (A1) and (A2), we find that

$$\begin{aligned} E\left[ \left| H\left( X_{t-\cdot }^{{\varepsilon }}\right) -H_n\left( X_{t-\cdot }^{{\varepsilon }}\right) \right| ^{{\gamma }} \right]&\le \int _{0}^{\delta }E\left[ \left| X_{t-s}^{{\varepsilon }}-X_{t-\lfloor ns \rfloor /n}^{{\varepsilon }}\right| ^{{\gamma }} \right] \,\mu (\textrm{d}s)\\&=O\left( n^{-{{\gamma }}}\right) +O\left( \varepsilon ^{{\gamma }} n^{-{{\gamma }}/2}\right) . \end{aligned}$$

$\square$

For the following Lemmas, we shall use the notations:

• (N11) let $R_{k-1}^{{\varepsilon }}$ denote a function $(0,1]\rightarrow {\mathbb {R}}$ for which there exist some constants $C_1$and $C_2$ such that

  $$\begin{aligned} \left| R_{k-1}^{{\varepsilon }}(a)\right| \le a{C_1}\left( 1+\Vert X_{t_{k-1}-\cdot }^{{\varepsilon }}\Vert _{\infty }\right) ^{C_2}, \end{aligned}$$

  for all $a > 0$ and $\varepsilon \in (0,1]$.

Lemma 5

Suppose the conditions (A1) and (A2). for ${{\gamma }}\ge 1$ and $t_{k-1}\le t\le t_k$, it holds that

$$\begin{aligned} E\left[ \left| X_t^\varepsilon -X_{t_{k-1}}^\varepsilon \right| ^{{\gamma }} +\left| H\left( X_{t-\cdot }^\varepsilon \right) -H\bigl (X_{t_{k-1}-\cdot }^\varepsilon \bigr )\right| ^{{\gamma }} \bigg |{\mathscr {F}}_{t_{k-1}}\right]&\le \Phi _p^\varepsilon (t)+R_{k-1}^{{\varepsilon }}\left( \left( t-t_{k-1}\right) ^{{\gamma }} \right) \\&\quad +R_{k-1}^{{\varepsilon }}\left( \varepsilon ^{{\gamma }} \left( t-t_{k-1}\right) ^{{{\gamma }}/2}\right) \end{aligned}$$

where $\Phi _p^\varepsilon (\cdot )$ is a function:

$$\begin{aligned} \Phi _p^\varepsilon (t)=C_{{\gamma }}\left\{ \int _{[t_{k-1},t_k]}\left| \phi ^\varepsilon (0)-\phi ^\varepsilon (t_{k-1}-s)\right| ^{{\gamma }} \,\mu (\textrm{d}s)+\int _{[0,\delta ]}\left| \phi ^\varepsilon (t-s)-\phi ^\varepsilon (t_{k-1}-s)\right| ^{{\gamma }} \,\mu (\textrm{d}s)\right\} . \end{aligned}$$

Proof

In the same way as Lemma 6 in Kessler (1997), we have

$$\begin{aligned} E\left[ \left| X_{t}^\varepsilon -X_{t_{k-1}}^\varepsilon \right| ^{{{\gamma }}}\bigg |{\mathscr {F}}_{t_{k-1}}\right]&\le C_{{\gamma }} \int _{t_{k-1}}^{t}E\left[ \left| X_{s}^\varepsilon -X_{t_{k-1}}^\varepsilon \right| ^{{{\gamma }}}+\left| H\left( X_{s-\cdot }^\varepsilon \right) -H\big (X_{t_{k-1}-\cdot }^\varepsilon \big )\right| ^{{{\gamma }}}\bigg |{\mathscr {F}}_{t_{k-1}}\right] \,\textrm{d}s\nonumber \\&\quad +R_{k-1}^{{\varepsilon }}\Big (\big (t-t_{k-1}\big )^{{\gamma }} \Big )+R_{k-1}^{{\varepsilon }}\Big (\varepsilon ^{{\gamma }} \big (t-t_{k-1}\big )^{{{\gamma }}/2}\Big ), \end{aligned}$$

(5.3)

where $C_{{\gamma }}$ is constant depending only on p. We find that

$$\begin{aligned} E\left[ \left| H\left( X_{t-\cdot }^\varepsilon \right) -H\big (X_{t_{k-1}-\cdot }^\varepsilon \big )\right| ^{{\gamma }} \bigg |{\mathscr {F}}_{t_{k-1}}\right] \le \int _0^\delta E\left[ \left| X_{t-s}^\varepsilon -X_{t_{k-1}-s}^\varepsilon \right| ^{{\gamma }} \bigg |{\mathscr {F}}_{t_{k-1}}\right] \,\mu (\textrm{d}s). \end{aligned}$$

Next, we consider three cases:

(b1) $t_{k-1}> s$;      (b2) $t_{k-1}\le s < t$;      (b3) $t\le s$.

(b1) In the same way as (5.3), we find that

$$\begin{aligned} E\left[ \left| X_{t-s}^\varepsilon -X_{t_{k-1}-s}^\varepsilon \right| ^{{\gamma }} \bigg |{\mathscr {F}}_{t_{k-1}}\right]&\le C_{{\gamma }}\int _{t_{k-1}-s}^{t-s}E\left[ \left| X_u^\varepsilon -X_{t_{k-1}}^\varepsilon \right| ^{{{\gamma }}}|{\mathscr {F}}_{t_{k-1}}\right] \,\textrm{d}u\nonumber \\&\quad +C_{{\gamma }}\int _{t_{k-1}-s}^{t-s}E\left[ \left| H\left( X_{u-\cdot }^\varepsilon \right) -H\big (X_{t_{k-1}-\cdot }^\varepsilon \big )\right| ^{{{\gamma }}}\bigg |{\mathscr {F}}_{t_{k-1}}\right] \,\textrm{d}u\nonumber \\&\quad +R_{k-1}^{{\varepsilon }}\Big (\big (t-t_{k-1}\big )^{{\gamma }} \Big )+R_{k-1}^{{\varepsilon }}\Big (\varepsilon ^{{\gamma }} \big (t-t_{k-1}\big )^{{{\gamma }}/2}\Big ). \end{aligned}$$

(5.4)

(b2) In the same way as (5.3),

$$\begin{aligned} E\left[ \left| X_{t-s}^\varepsilon -X_{t_{k-1}-s}^\varepsilon \right| ^{{\gamma }} \bigg |{\mathscr {F}}_{t_{k-1}}\right]&= E\left[ \left| X_{t-s}^\varepsilon -\phi ^\varepsilon (t_{k-1}-s)\right| ^{{\gamma }} \bigg |{\mathscr {F}}_{t_{k-1}}\right] \nonumber \\&\le 2^{{{\gamma }}-1}\left( E\left[ \left| X_{t-s}^\varepsilon -X_0^\varepsilon \right| ^{{\gamma }} \bigg |{\mathscr {F}}_{t_{k-1}}\right] +\left| \phi ^\varepsilon (0)-\phi ^\varepsilon (t_{k-1}-s)\right| ^{{\gamma }} \right) \nonumber \\&\le {\tilde{C}}_p\int _{0}^{t-s}E\left[ \left| X_{u}^\varepsilon -X_{t_{k-1}}^\varepsilon \right| ^{{{\gamma }}}+\left| H\left( X_{u-\cdot }^\varepsilon \right) -H\big (X_{t_{k-1}-\cdot }^\varepsilon \big )\right| ^{{{\gamma }}}\bigg |{\mathscr {F}}_{t_{k-1}}\right] \,\textrm{d}u \nonumber \\&\quad +2^{{{\gamma }}-1}|\phi ^\varepsilon (0)-\phi ^\varepsilon (t_{k-1}-s)|^{{\gamma }} \nonumber \\&\quad +R_{k-1}^{{\varepsilon }}\Big (\big (t-t_{k-1}\big )^{{\gamma }} \Big )+R_{k-1}^{{\varepsilon }}\Big (\varepsilon ^{{\gamma }} \big (t-t_{k-1}\big )^{{{\gamma }}/2}\Big ), \end{aligned}$$

(5.5)

where ${\tilde{C}}_p$ is constant depending only on p.

(b3) It is easy to find that

$$\begin{aligned} E\left[ \left| X_{t-s}^\varepsilon -X_{t_{k-1}-s}^\varepsilon \right| ^{{\gamma }} \bigg |{\mathscr {F}}_{t_{k-1}}\right] =\left| \phi ^{\varepsilon }(t-s)-\phi ^{\varepsilon }(t_{k-1}-s)\right| ^{{\gamma }}. \end{aligned}$$

(5.6)

From (5.4), (5.5) and (5.6), we have

$$\begin{aligned}&E\left[ \left| H\left( X_{t-\cdot }^\varepsilon \right) -H\big (X_{t_{k-1}-\cdot }^\varepsilon \big )\right| ^{{\gamma }} \bigg |{\mathscr {F}}_{t_{k-1}}\right] \\&\le C_{{\gamma }}\bigg \{\mu \left( \left[ 0,\delta \right] \right) \int _{0}^{t}E\left[ \left| X_{u}^\varepsilon -X_{t_{k-1}}^\varepsilon \right| ^{{{\gamma }}}\bigg |{\mathscr {F}}_{t_{k-1}}\right] \,\textrm{d}u\\&\qquad +\mu \left( \left[ 0,\delta \right] \right) \int _{0}^{t}E\left[ \left| H\left( X_{u-\cdot }^\varepsilon \right) -H\big (X_{t_{k-1}-\cdot }^\varepsilon \big )\right| ^{{{\gamma }}}\bigg |{\mathscr {F}}_{t_{k-1}}\right] \,\textrm{d}u\\&\qquad +\int _{[t_{k-1},t_k]}\left| \phi ^\varepsilon (0)-\phi ^\varepsilon (t_{k-1}-s)\right| ^{{\gamma }} \,\mu \left( \textrm{d}s\right) \\&\qquad +\int _{[0,\delta ]}\left| \phi ^\varepsilon (t-s)-\phi ^\varepsilon (t_{k-1}-s)\right| ^{{\gamma }} \,\mu \left( \textrm{d}s\right) \bigg \}\\&\quad +R_{k-1}^{{\varepsilon }}\Big (\big (t-t_{k-1}\big )^{{\gamma }} \Big )+R_{k-1}^{{\varepsilon }}\Big (\varepsilon ^{{\gamma }} \big (t-t_{k-1}\big )^{{{\gamma }}/2}\Big ). \end{aligned}$$

By (A1), (5.3), and Gronwall’s inequality, we obtain the conclusion. $\square$

Remark 3

Lemma 5 is satisfied for $t_{k-1}\ge \delta$ and for $t\ge \delta$.

For Lemma 6, we use some abbreviations:

• (N12) Denote by $b^i_{t,H}=b^i\left( X_t^\varepsilon ,H\left( X_{t-\cdot }^\varepsilon \right) ,\theta _0\right)$ and

  $$\begin{aligned}{}[\sigma \sigma ^\top ]_{t,H}^{ij}=[\sigma \sigma ^\top ]^{ij}\left( X_t^\varepsilon ,H\left( X_{t-\cdot }^\varepsilon \right) ,\beta _0\right) \end{aligned}$$

  for $\left\{ b^i\right\}$ and $\left\{ [\sigma \sigma ^{\top }]^{ij}\right\}$.

Lemma 6

Suppose the condition (A1). Then the following (i)-(iv) hold true:

• (i)
  $$\begin{aligned} E\left[ P_{k}^{i_{1}}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right] =\frac{1}{n}\left( b^{i_{1}}_{t_{k-1},H}-b^{i_{1}}_{t_{k-1},H_n}\right) +\int _{t_{k-1}}^{t_k}\Phi _1^\varepsilon (s)~ds+R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^2}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n\sqrt{n}}\right) . \end{aligned}$$
• (ii)
  $$\begin{aligned} E\left[ P_{k}^{i_{1}}P_{k}^{i_{2}}\left( \theta _{0}\right) \Big |{\mathscr {F}}_{t_{k-1}}\right]&= \frac{\varepsilon ^{2}}{n}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{1}i_{2}}+\frac{1}{n^2}\left( b_{t_{k-1},H}^{i_1}-b_{t_{k-1},H_n}^{i_1}\right) \left( b_{t_{k-1},H}^{i_2}-b_{t_{k-1},H_n}^{i_2}\right) \\&\quad +\int _{t_{k-1}}^{t_k}\left\{ \Phi _2^\varepsilon (s)+\varepsilon ^2\Phi _1^\varepsilon (s)\right\} \,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n}\right) \int _{t_{k-1}}^{t_k}\Phi _1^\varepsilon (s)\,\textrm{d}s+R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\Phi _1^\varepsilon (u)\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^3}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n^2\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^2}{n^2}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^3}{n\sqrt{n}}\right) . \end{aligned}$$
• (iii)
  $$\begin{aligned} E\left[ P_{k}^{i_{1}}P_{k}^{i_{2}}P_{k}^{i_{3}}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right]&= \frac{1}{n^3}\left( b_{t_{k-1},H}^{i_1}-b_{t_{k-1},H_n}^{i_1}\right) \left( b_{t_{k-1},H}^{i_2}-b_{t_{k-1},H_n}^{i_2}\right) \left( b_{t_{k-1},H}^{i_3}-b_{t_{k-1},H_n}^{i_3}\right) \\&\quad +\frac{\varepsilon ^2}{2n^2}\sum _{{\tilde{\sigma }}\in G(3)}[\sigma \sigma ^\top ]^{i_{{\tilde{\sigma }}(1)}i_{{\tilde{\sigma }}(2)}}\left( b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(3)}}-b_{t_{k-1},H_n}^{i_{{\tilde{\sigma }}(3)}}\right) \\&\quad +\int _{t_{k-1}}^{t_k}\left\{ \Phi _3^\varepsilon (s)+\varepsilon ^2\Phi _2^\varepsilon (s)\right\} \,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n}\right) \int _{t_{k-1}}^{t_k}\{\Phi _2^\varepsilon (s)+\varepsilon ^2\Phi _1^\varepsilon (s)\}\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^2}\right) b_{t_{k-1},H_n}^{i_{{\tilde{\sigma }}(2)}}\int _{t_{k-1}}^{t_k}\Phi _1^\varepsilon (s)\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\{\Phi _2^\varepsilon (u)+\varepsilon ^2\Phi _1^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n}\right) \int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^s\Phi _1^\varepsilon (u)\,\textrm{d}u\,\textrm{d}s\\&\quad +\sum _{{\tilde{\sigma }}\in G(3)}b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(1)}}b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(2)}}\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\int _{t_{k-1}}^{u}\Phi _1^\varepsilon (v)\,\textrm{d}v\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^4}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n^3\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^2}{n^3}\right) \\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^3}{n^2\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^4}{n^2}\right) . \end{aligned}$$
• (iv)
  $$\begin{aligned} E\left[ P_{k}^{i_{1}}P_{k}^{i_{2}}P_{k}^{i_{3}}P_{k}^{i_{4}}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right]&= \frac{\varepsilon ^4}{n^2}\Bigg ([\sigma \sigma ^\top ]_{t_{k-1},H}^{i_1i_2}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_3i_4}+[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_1i_3}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_2i_4}\\&\qquad +[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_1i_4}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_2i_3}\Bigg )\\&\quad +\frac{1}{n^4}\left( b_{t_{k-1},H}^{i_1}-b_{t_{k-1},H_n}^{i_1}\right) \left( b_{t_{k-1},H}^{i_2}-b_{t_{k-1},H_n}^{i_2}\right) \times \\&\qquad \left( b_{t_{k-1},H}^{i_3}-b_{t_{k-1},H_n}^{i_3}\right) \left( b_{t_{k-1},H}^{i_4}-b_{t_{k-1},H_n}^{i_4}\right) \\&\quad +\frac{\varepsilon ^2}{4n^3}\sum _{{\tilde{\sigma }}\in G(4)}[\sigma \sigma ^{\top }]^{i_{{\tilde{\sigma }}(1)}i_{{\tilde{\sigma }}(2)}}\left( b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(3)}}-b_{t_{k-1},H_n}^{i_{{\tilde{\sigma }}(3)}}\right) \\&\qquad \left( b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(4)}}-b_{t_{k-1},H_n}^{i_{{\tilde{\sigma }}(4)}}\right) \\&\quad +\int _{t_{k-1}}^{t_k}\left\{ \Phi _4^\varepsilon (s)+\varepsilon ^2\Phi _3^\varepsilon (s)\right\} \,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n}\right) \int _{t_{k-1}}^{t_k}\{\Phi _3^\varepsilon (u)+\varepsilon ^2\Phi _2^\varepsilon (s)\}\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^2}\right) \int _{t_{k-1}}^{t_k}\{\Phi _2^\varepsilon (s)+\varepsilon ^2\Phi _1^\varepsilon (s)\}\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{s}\{\Phi _3^\varepsilon (u)+\varepsilon ^2\Phi _2^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n}\right) \int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\{\Phi _2^\varepsilon (u)+\varepsilon ^2\Phi _1^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(\varepsilon ^2)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\{\Phi _2^\varepsilon (u)+\varepsilon ^2\Phi _1^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\int _{t_{k-1}}^{u}\left\{ \Phi _2^\varepsilon (v)+\varepsilon ^2\Phi _1^\varepsilon (v)\right\} \,\textrm{d}v\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^s\int _{t_{k-1}}^u\int _{t_{k-1}}^v\Phi _1^\varepsilon (w)\,\textrm{d}w\,\textrm{d}v\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^5}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n^4\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^2}{n^4}\right) \\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^3}{n^3\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^4}{n^3}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^5}{n^2\sqrt{n}}\right) . \end{aligned}$$

Proof

(i) It is satisfied from the Lipschitz condition on b in (A1) that

$$\begin{aligned} E\left[ \left( \Delta _kX^\varepsilon \right) ^{i_{1}}-\frac{1}{n}b_{t_{k-1},H}^{i_{1}}\bigg |{\mathscr {F}}_{t_{k-1}}\right]&= E\left[ \int _{t_{k-1}}^{t_{k}}\left( b_{s,H}^{i_{1}}-b_{t_{k-1},H}^{i_{1}}\right) \,\textrm{d}s \bigg |{\mathscr {F}}_{t_{k-1}}\right] \\&\le E\left[ \int _{t_{k-1}}^{t_{k}}\left| b_{s,H}^{i_{1}}-b_{t_{k-1},H}^{i_{1}}\right| \,\textrm{d}s \bigg |{\mathscr {F}}_{t_{k-1}}\right] \\&\le E\left[ \int _{t_{k-1}}^{t_{k}}\left\{ \left| X_{s}^\varepsilon -X_{t_{k-1}}^\varepsilon \right| +\left| H\left( X_{s-\cdot }^\varepsilon \right) -H\big (X_{t_{k-1}-\cdot }^\varepsilon \big )\right| \right\} \,\textrm{d}s \bigg |{\mathscr {F}}_{t_{k-1}} \right] .\\ \end{aligned}$$

From Lemma 5, the proof of (i) is completed. (ii) We find that

$$\begin{aligned} E\left[ \prod _{j=1}^2\left( \Delta _kX^\varepsilon \right) ^{i_j}\Bigg |{\mathscr {F}}_{t_{k-1}}\right]&= E\left[ \int _{t_{k-1}}^{t_{k}}\left\{ \sum _{{\tilde{\sigma }}\in G(2)}\left( \Delta _sX^\varepsilon \right) ^{i_{{\tilde{\sigma }}(1)}}b_{s,H}^{i_{{\tilde{\sigma }}(2)}}+\varepsilon ^{2}[\sigma \sigma ^\top ]_{s,H}^{i_{1}i_{2}}\right\} \,\textrm{d}s\Bigg |{\mathscr {F}}_{t_{k-1}}\right] \\&= \sum _{{\tilde{\sigma }}\in G(2)}E\left[ \int _{t_{k-1}}^{t_{k}}\left( \Delta _sX^\varepsilon \right) ^{i_{{\tilde{\sigma }}(1)}}\left( b_{s,H}-b_{t_{k-1},H}\right) ^{i_{{\tilde{\sigma }}(2)}}\,\textrm{d}s\Bigg |{\mathscr {F}}_{t_{k-1}}\right] \\&\quad +\sum _{{\tilde{\sigma }}\in G(2)}E\left[ \int _{t_{k-1}}^{t_{k}}\left( \Delta _sX^\varepsilon \right) ^{i_{{\tilde{\sigma }}(1)}}\,\textrm{d}s\Bigg |{\mathscr {F}}_{t_{k-1}}\right] b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(2)}}\\&\quad +\varepsilon ^{2}E\left[ \int _{t_{k-1}}^{t_{k}}\left\{ [\sigma \sigma ^\top ]_{s,H}^{i_{1}i_{2}}-[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{1}i_{2}}\right\} \,\textrm{d}s\Bigg |{\mathscr {F}}_{t_{k-1}}\right] \\&\quad +\varepsilon ^{2}n^{-1}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{1}i_{2}}. \end{aligned}$$

It follows from the Lipschitz condition on b in (A1) that

$$\begin{aligned} E\left[ \int _{t_{k-1}}^{t_{k}}\left( \Delta _sX^\varepsilon \right) ^{i_{1}}\{b_{s,H}^{i_{2}}-b_{t_{k-1},H}^{i_{2}}\}\,\textrm{d}s\bigg |{\mathscr {F}}_{t_{k-1}}\right]&\le 2K\int _{t_{k-1}}^{t_{k}}E\left[ \left| X_{s}^\varepsilon -X_{t_{k-1}}^\varepsilon \right| ^{2}\bigg |{\mathscr {F}}_{t_{k-1}}\right] \,\textrm{d}s\\&\quad +2K\int _{t_{k-1}}^{t_{k}}E\left[ \left| H\left( X_{s-\cdot }^\varepsilon \right) -H\big (X_{t_{k-1}-\cdot }^\varepsilon \big )\right| ^{2}\bigg |{\mathscr {F}}_{t_{k-1}}\right] \,\textrm{d}s. \end{aligned}$$

From Lemma 5, we have

$$\begin{aligned}&E\left[ \int _{t_{k-1}}^{t_{k}}\left( \Delta _sX^\varepsilon \right) ^{i_{1}}\left\{ b_{s,H}^{i_{2}}-b_{t_{k-1},H}^{i_{2}}\right\} \,\textrm{d}s\bigg |{\mathscr {F}}_{t_{k-1}}\right] = \int _{t_{k-1}}^{t_k}\Phi _2^\varepsilon (s)\, \textrm{d}s\nonumber \\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^3}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^2}{n^2}\right) . \end{aligned}$$

(5.7)

From the same argument of (5.7), it holds that

$$\begin{aligned} \varepsilon ^{2}E\left[ \int _{t_{k-1}}^{t_{k}}\left\{ [\sigma \sigma ^\top ]_{s,H}^{i_{1}i_{2}}-[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{1}i_{2}}\right\} \,\textrm{d}s\bigg |{\mathscr {F}}_{t_{k-1}}\right]&= \varepsilon ^2\int _{t_{k-1}}^{t_k}\Phi _1^\varepsilon (s)\,\textrm{d}s\nonumber \\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^{2}}{n^2}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^3}{n\sqrt{n}}\right) . \end{aligned}$$

(5.8)

It is satisfied from the proof of (i) that

$$\begin{aligned} E\left[ \left( \Delta _sX^\varepsilon \right) ^{i_{1}}\Big |{\mathscr {F}}_{t_{k-1}}\right]&=(s-t_{k-1})b_{t_{k-1},H}^{i_{1}}+\int _{t_{k-1}}^s\Phi _1^\varepsilon (u)\,\textrm{d}u\\&\quad +R_{k-1}^{{\varepsilon }}\left( \left( s-t_{k-1}\right) ^{2}\right) +R_{k-1}^{{\varepsilon }}\left( \varepsilon \left( s-t_{k-1}\right) ^{3/2}\right) . \end{aligned}$$

Therefore,

$$\begin{aligned} E\left[ \int _{t_{k-1}}^{t_{k}}\left( \Delta _sX^\varepsilon \right) ^{i_{1}}\,\textrm{d}s\bigg |{\mathscr {F}}_{t_{k-1}}\right] b_{t_{k-1},H}^{i_{2}}&= \frac{1}{2n^{2}}b_{t_{k-1},H}^{i_{1}}b_{t_{k-1},H}^{i_{2}}+b_{t_{k-1},H}^{i_{2}}\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\Phi _1^\varepsilon (u)\,\textrm{d}u\,\textrm{d}s\nonumber \\&\quad +R_{k-1}^{{\varepsilon }}\left( n^{-3}\right) +R_{k-1}^{{\varepsilon }}\left( \varepsilon n^{-5/2}\right) . \end{aligned}$$

(5.9)

It follows from (5.7–5.9) that

$$\begin{aligned} E\left[ \prod _{j=1}^2\left( \Delta _kX^\varepsilon \right) ^{i_j}\Bigg |{\mathscr {F}}_{t_{k-1}}\right]&= \frac{\varepsilon ^{2}}{n}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{1}i_{2}}+ \frac{1}{n^{2}}b_{t_{k-1},H}^{i_{1}}b_{t_{k-1},H}^{i_{2}}+\int _{t_{k-1}}^{t_k}\left\{ \Phi _2^\varepsilon (s)+\varepsilon ^2\Phi _1^\varepsilon (s)\right\} \,\textrm{d}s\\&\quad +\left\{ b_{t_{k-1},H}^{i_{1}}+b_{t_{k-1},H}^{i_{2}}\right\} \int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\Phi _1^\varepsilon (u)\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^3}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n^2\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^2}{n^2}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^{3}}{n\sqrt{n}}\right) . \end{aligned}$$

Therefore,

$$\begin{aligned} E\left[ P_{k}^{i_{1}}P_{k}^{i_{2}}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right]&= E\left[ \left( \Delta _kX^\varepsilon \right) ^{i_{1}}\left( \Delta _kX^\varepsilon \right) ^{i_{2}}\Big |{\mathscr {F}}_{t_{k-1}}\right] \\&\quad -\sum _{{\tilde{\sigma }}\in G(2)}E\left[ \left( \Delta _kX^\varepsilon \right) ^{i_{{\tilde{\sigma }}(1)}}\Big |{\mathscr {F}}_{t_{k-1}}\right] \frac{1}{n}b_{t_{k-1},H_n}^{i_{{\tilde{\sigma }}(2)}}+\frac{1}{n^{2}}b_{t_{k-1},H_n}^{i_{1}}b_{t_{k-1},H_n}^{i_{2}}\\&= \frac{\varepsilon ^{2}}{n}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{1}i_{2}}+ \frac{1}{n^{2}}b_{t_{k-1},H}^{i_{1}}b_{t_{k-1},H}^{i_{2}}+\int _{t_{k-1}}^{t_k}\left\{ 4\Phi _2^\varepsilon (s)+\varepsilon ^2\Phi _1^\varepsilon (s)\right\} \,\textrm{d}s\\&\quad +\left( b_{t_{k-1},H}^{i_{1}}+b_{t_{k-1},H}^{i_{2}}\right) \int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\Phi _1^\varepsilon (u)\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^3}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n^2\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^2}{n^2}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^{3}}{n\sqrt{n}}\right) \\&\quad -\sum _{{\tilde{\sigma }}\in G(2)}\frac{1}{n}b_{t_{k-1},H_n}^{i_{{\tilde{\sigma }}(2)}}\bigg \{\frac{1}{n}b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(1)}}+\int _{t_{k-1}}^{t_k}\Phi _1^\varepsilon (s)\,\textrm{d}s\\&\qquad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^2}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n\sqrt{n}}\right) \bigg \}\\&\quad +\frac{1}{n^{2}}b_{t_{k-1},H_n}^{i_{1}}b_{t_{k-1},H_n}^{i_{2}}\\&= \frac{\varepsilon ^{2}}{n}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{1}i_{2}}+\frac{1}{n^2}\left( b_{t_{k-1},H}^{i_1}-b_{t_{k-1},H_n}^{i_1}\right) \left( b_{t_{k-1},H}^{i_2}-b_{t_{k-1},H_n}^{i_2}\right) \\&\quad +\int _{t_{k-1}}^{t_k}\left\{ \Phi _2^\varepsilon (s)+\varepsilon ^2\Phi _1^\varepsilon (s)\right\} \,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\Phi _1^\varepsilon (u)\,\textrm{d}u\,\textrm{d}s+R_{k-1}^{{\varepsilon }}\left( \frac{1}{n}\right) \int _{t_{k-1}}^{t_k}\Phi _1^\varepsilon (s)\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^3}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n^2\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^2}{n^2}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^{3}}{n\sqrt{n}}\right) . \end{aligned}$$

(iii) From the same argument as the proof of (ii), it holds that

$$\begin{aligned} E\left[ \prod _{j=1}^3\left( \Delta _kX^\varepsilon \right) ^{i_j}\Bigg |{\mathscr {F}}_{t_{k-1}}\right]&= \frac{\varepsilon ^2}{2n^2}\sum _{{\tilde{\sigma }}\in G(3)}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{{\tilde{\sigma }}(1)}i_{{\tilde{\sigma }}(2)}}b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(3)}}+\frac{1}{n^3}b_{t_{k-1},H}^{i_{1}}b_{t_{k-1},H}^{i_{2}}b_{t_{k-1},H}^{i_{3}}\\&\quad +\int _{t_{k-1}}^{t_k}\{\Phi _3^\varepsilon (s)+\varepsilon ^2\Phi _2^\varepsilon (s)\}\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\{\Phi _2^\varepsilon (u)+\varepsilon ^2\Phi _1^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\int _{t_{k-1}}^{u}\Phi _1^\varepsilon (v)\,\textrm{d}v\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^4}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n^3\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^2}{n^3}\right) \\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^3}{n^2\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^4}{n^2}\right) , \end{aligned}$$

and

$$\begin{aligned} E\left[ P_{k}^{i_{1}}P_{k}^{i_{2}}P_{k}^{i_{3}}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right]&= E\left[ \prod _{j=1}^3\left( \Delta _kX^\varepsilon \right) ^{i_j}\Bigg |{\mathscr {F}}_{t_{k-1}}\right] -E[(\Delta _kX^\varepsilon )^{i_{1}}(\Delta _kX^\varepsilon )^{i_{3}}|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n}b_{t_{k-1},H_n}^{i_{2}}\\&\quad -E[(\Delta _kX^\varepsilon )^{i_{2}}(\Delta _kX^\varepsilon )^{i_{3}}|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n}b_{t_{k-1},H_n}^{i_{1}}\\&\quad +E[(\Delta _kX^\varepsilon )^{i_{3}}|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n^2}b_{t_{k-1},H_n}^{i_{1}}b_{t_{k-1},H_n}^{i_2}\\&\quad -E[P_{k}^{i_1}P_{k}^{i_2}(\theta _{0})|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n}b_{t_{k-1},H_n}^{i_3}\\&= \frac{1}{n^3}\prod _{j=1}^3\left( b_{t_{k-1},H}^{i_j}-b_{t_{k-1},H_n}^{i_j}\right) \\&\quad +\frac{\varepsilon ^2}{2n^2}\sum _{{\tilde{\sigma }}\in G(3)}[\sigma \sigma ^\top ]^{i_{{\tilde{\sigma }}(1)}i_{{\tilde{\sigma }}(2)}}\left( b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(3)}}-b_{t_{k-1},H_n}^{i_{{\tilde{\sigma }}(3)}}\right) \\&\quad +\int _{t_{k-1}}^{t_k}\{\Phi _3^\varepsilon (s)+\varepsilon ^2\Phi _2^\varepsilon (s)\}\,\textrm{d}s+R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^2}\right) \int _{t_{k-1}}^{t_k}\Phi _1^\varepsilon (s)\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n}\right) \int _{t_{k-1}}^{t_k}\{\Phi _2^\varepsilon (s)+\varepsilon ^2\Phi _1^\varepsilon (s)\}\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\{\Phi _2^\varepsilon (u)+\varepsilon ^2\Phi _1^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n}\right) \int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^s\Phi _1^\varepsilon (u)\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\int _{t_{k-1}}^{u}\Phi _1^\varepsilon (v)\,\textrm{d}v\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^4}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n^3\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^2}{n^3}\right) \\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^3}{n^2\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^4}{n^2}\right) . \end{aligned}$$

(iv) It follows from the same argument as the proof of (ii) that

$$\begin{aligned} E\left[ \prod _{j=1}^4\left( \Delta _kX^\varepsilon \right) ^{i_j}\Bigg |{\mathscr {F}}_{t_{k-1}}\right]&= \frac{\varepsilon ^4}{8n^2}\sum _{{\tilde{\sigma }}\in G(4)}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{{\tilde{\sigma }}(1)}i_{{\tilde{\sigma }}(2)}}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{{\tilde{\sigma }}(3)}i_{{\tilde{\sigma }}(4)}}\\&\quad +\frac{\varepsilon ^2}{4n^3}\sum _{{\tilde{\sigma }}\in G(4)}[\sigma \sigma ^{\top }]_{t_{k-1},H}^{i_{{\tilde{\sigma }}(1)}i_{{\tilde{\sigma }}(2)}}b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(3)}}b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(4)}}+\frac{1}{n^4}\prod _{j=1}^4b_{t_{k-1},H}^{i_j}\\&\quad +\int _{t_{k-1}}^{t_k}\left\{ \Phi _4^\varepsilon (s)+\varepsilon ^2\Phi _3^\varepsilon (s)\right\} \,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\{\Phi _3^\varepsilon (u)+\varepsilon ^2\Phi _2^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(\varepsilon ^2)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\{\Phi _2^\varepsilon (u)+\varepsilon ^2\Phi _1^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\int _{t_{k-1}}^{u}\left\{ \Phi _2^\varepsilon (v)+\varepsilon ^2\Phi _1^\varepsilon (v)\right\} \,\textrm{d}v\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^s\int _{t_{k-1}}^u\int _{t_{k-1}}^v\Phi _1^\varepsilon (w)\,\textrm{d}w\,\textrm{d}v\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\Big (\frac{1}{n^5}\Big )+R_{k-1}^{{\varepsilon }}\Big (\frac{\varepsilon }{n^4\sqrt{n}}\Big )+R_{k-1}^{{\varepsilon }}\Big (\frac{\varepsilon ^2}{n^4}\Big )\\&\quad +R_{k-1}^{{\varepsilon }}\Big (\frac{\varepsilon ^3}{n^3\sqrt{n}}\Big )+R_{k-1}^{{\varepsilon }}\Big (\frac{\varepsilon ^4}{n^3}\Big )+R_{k-1}^{{\varepsilon }}\Big (\frac{\varepsilon ^5}{n^2\sqrt{n}}\Big ), \end{aligned}$$

and

$$\begin{aligned} E\left[ P_{k}^{i_{1}}P_{k}^{i_{2}}P_{k}^{i_{3}}P_{k}^{i_{4}}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right]&= E\left[ \prod _{j=1}^4\left( \Delta _kX^\varepsilon \right) ^{i_j}\Bigg |{\mathscr {F}}_{t_{k-1}}\right] \\&\quad -E[(\Delta _kX^\varepsilon )^{i_{1}}(\Delta _kX^\varepsilon )^{i_{2}}(\Delta _kX^\varepsilon )^{i_{4}}|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n}b_{t_{k-1},H_n}^{i_{3}}\\&\quad -E[(\Delta _kX^\varepsilon )^{i_{1}}(\Delta _kX^\varepsilon )^{i_{3}}(\Delta _kX^\varepsilon )^{i_{4}}|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n}b_{t_{k-1},H_n}^{i_{2}}\\&\quad -E[(\Delta _kX^\varepsilon )^{i_{2}}(\Delta _kX^\varepsilon )^{i_{3}}(\Delta _kX^\varepsilon )^{i_{4}}|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n}b_{t_{k-1},H_n}^{i_{1}}\\&\quad +E[(\Delta _kX^\varepsilon )^{i_{1}}(\Delta _kX^\varepsilon )^{i_{4}}|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n^2}b_{t_{k-1},H_n}^{i_{2}}b_{t_{k-1},H_n}^{i_{3}}\\&\quad +E[(\Delta _kX^\varepsilon )^{i_{2}}(\Delta _kX^\varepsilon )^{i_{4}}|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n^2}b_{t_{k-1},H_n}^{i_{1}}b_{t_{k-1},H_n}^{i_{3}}\\&\quad +E[(\Delta _kX^\varepsilon )^{i_{3}}(\Delta _kX^\varepsilon )^{i_{4}}|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n^2}b_{t_{k-1},H_n}^{i_{1}}b_{t_{k-1},H_n}^{i_{2}}\\&\quad -E[(\Delta _kX^\varepsilon )^{i_{4}}|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n^3}b_{t_{k-1},H_n}^{i_{1}}b_{t_{k-1},H_n}^{i_{2}}b_{t_{k-1},H_n}^{i_3}\\&\quad -E[P_{k}^{i_{1}}P_{k}^{i_{2}}P_{k}^{i_{3}}(\theta _{0})|{\mathscr {F}}_{t_{k-1}}]\frac{1}{n}b_{t_{k-1},H_n}^{i_4}\\&= \frac{\varepsilon ^4}{8n^2}\sum _{{\tilde{\sigma }}\in G(4)}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{{\tilde{\sigma }}(1)}i_{{\tilde{\sigma }}(2)}}[\sigma \sigma ^\top ]_{t_{k-1},H}^{i_{{\tilde{\sigma }}(3)}i_{{\tilde{\sigma }}(4)}}\\&\quad +\frac{1}{n^4}\prod _{j=1}^4\left( b_{t_{k-1},H}^{i_j}-b_{t_{k-1},H_n}^{i_j}\right) \\&\quad +\frac{\varepsilon ^2}{4n^3}\sum _{{\tilde{\sigma }}\in G(4)}[\sigma \sigma ^{\top }]^{i_{{\tilde{\sigma }}(1)}i_{{\tilde{\sigma }}(2)}}\left( b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(3)}}-b_{t_{k-1},H_n}^{i_{{\tilde{\sigma }}(3)}}\right) \\&\qquad \left( b_{t_{k-1},H}^{i_{{\tilde{\sigma }}(4)}}-b_{t_{k-1},H_n}^{i_{{\tilde{\sigma }}(4)}}\right) \\&\quad +\int _{t_{k-1}}^{t_k}\left\{ \Phi _4^\varepsilon (s)+\varepsilon ^2\Phi _3^\varepsilon (s)\right\} \,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n}\right) \int _{t_{k-1}}^{t_k}\{\Phi _3^\varepsilon (u)+\varepsilon ^2\Phi _2^\varepsilon (s)\}\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^2}\right) \int _{t_{k-1}}^{t_k}\{\Phi _2^\varepsilon (s)+\varepsilon ^2\Phi _1^\varepsilon (s)\}\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{s}\{\Phi _3^\varepsilon (u)+\varepsilon ^2\Phi _2^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n}\right) \int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\{\Phi _2^\varepsilon (u)+\varepsilon ^2\Phi _1^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(\varepsilon ^2)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\{\Phi _2^\varepsilon (u)+\varepsilon ^2\Phi _1^\varepsilon (u)\}\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\int _{t_{k-1}}^{u}\left\{ \Phi _2^\varepsilon (v)+\varepsilon ^2\Phi _1^\varepsilon (v)\right\} \,\textrm{d}v\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^s\int _{t_{k-1}}^u\int _{t_{k-1}}^v\Phi _1^\varepsilon (w)\,\textrm{d}w\,\textrm{d}v\,\textrm{d}u\,\textrm{d}s\\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^5}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n^4\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^2}{n^4}\right) \\&\quad +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^3}{n^3\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^4}{n^3}\right) +R_{k-1}^{{\varepsilon }}\Big (\frac{\varepsilon ^5}{n^2\sqrt{n}}\Big ). \end{aligned}$$

$\square$

We shall use the notation:

• (N13) We denote the gradient operator of $f(x,y,\theta )$ with respect to x by

  $$\begin{aligned} \triangledown _xf(x,y,\theta )=\left( \partial _{x_1}f(x,y,\theta ),\dots \partial _{x_d}f(x,y,\theta )\right) ^{\top }. \end{aligned}$$

In Lemma 7, the proof ideas follow Long et al. (2013)

Lemma 7

Let $f\in C_{\uparrow }^{1,1,1}({\mathbb {R}}^d\times {\mathbb {R}}^d\times \Theta )$ and suppose the conditions (A1)–(A3). Then the following (i) and (ii) hold true:

• (i) As $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$,

  $$\begin{aligned} \frac{1}{n}\sum _{k=1}^{n}f\left( X_{t_{k-1}}^{\varepsilon }, H_n\big (X_{t_{k-1}-\cdot }^{\varepsilon }\big ),\theta \right) \xrightarrow {P}\int _{0}^{1}f\left( X_{s}^0,H\big (X_{s-\cdot }^0\big ),\theta \right) \,\textrm{d}s, \end{aligned}$$

  uniformly in $\theta \in \Theta$.

• (ii) As $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$,

  $$\begin{aligned} \sum _{k=1}^{n}f\left( X_{t_{k-1}}^{\varepsilon },H_n\big (X_{t_{k-1}-\cdot }^{\varepsilon }\big ),\theta \right) P_k(\theta _0)\xrightarrow {P}0, \end{aligned}$$

  uniformly in $\theta \in \Theta$.

Proof

(i) From lemma 2, Lemma 3 and Taylor’s formula, we find that

$$\begin{aligned}&\sup _{\theta \in \Theta }\left| \frac{1}{n}\sum _{k=1}^{n}f\left( X_{t_{k-1}}^\varepsilon ,H_n\big (X_{t_{k-1}-\cdot }^\varepsilon \big ),\theta \right) -\int _{0}^{1}f\left( X_{s}^0,H\big (X_{s-\cdot }^0\big ),\theta \right) \,\textrm{d}s\right| \\ =&\sup _{\theta \in \Theta }\left| \int _{0}^{1}\left\{ f\left( Y_{s}^{n,\varepsilon },H_n\big (Y_{s-\cdot }^{n,\varepsilon }\big ),\theta \right) -f\left( X_{s}^0,H\big (X_{s-\cdot }^0\big ),\theta \right) \right\} \,\textrm{d}s\right| \\ \le&\sup _{\theta \in \Theta }\int _0^1\int _0^1\Big |(\triangledown _xf)^\top \left( X_s^0+u\left( Y_s^{n,\varepsilon }-X_s^0\right) ,H\big (X_{s-\cdot }^0\big )+u\left( H_n\big (Y_{s-\cdot }^{n,\varepsilon }\big )-H\big (X_{s-\cdot }^0\big )\right) ,\theta \right) \\&\quad \cdot \left( Y_s^{n,\varepsilon }-X_s^0\right) +(\triangledown _yf)^\top \left( X_s^0+u\left( Y_s^{n,\varepsilon }-X_s^0\right) ,H\big (X_{s-\cdot }^0\big )+u\left( H_n\big (Y_{s-\cdot }^{n,\varepsilon }\big )-H\big (X_{s-\cdot }^0\big )\right) ,\theta \right) \\&\quad \cdot \left( H_n\big (Y_{s-\cdot }^{n,\varepsilon }\big )-H\big (X_{s-\cdot }^0\big )\right) \Big |\,\textrm{d}u\,\textrm{d}s\\ \le&\int _0^1C\left\{ 1+\left| X_s^0\right| +\left| Y_s^{n,\varepsilon }\right| +\mu \left( \left[ 0,\delta \right] \right) \left( \left\| X_{s-\cdot }^0\right\| _\infty +\left\| Y_{s-\cdot }^{n,\varepsilon }\right\| _\infty \right) \right\} ^\lambda \Big (\left| Y_s^{n,\varepsilon }-X_s^0\right| \\&\quad +\left| H_n\big (Y_{s-\cdot }^{n,\varepsilon }\big )-H\big (Y_{s-\cdot }^{n,\varepsilon }\big )\right| +\mu \left( \left[ 0,\delta \right] \right) \left\| Y_{s-\cdot }^{n,\varepsilon }-X_{s-\cdot }^0\right\| _\infty \Big )\,\textrm{d}s\\ \le&~C\Big (1+\big (1+\mu ([0,\delta ])\big )\big (\sup _{-\delta \le s\le 1}|X_{s}^0|+\sup _{-\delta \le s\le 1}|Y_{s}^{n,\varepsilon }|\big )\Big )^\lambda \Big \{\sup _{0\le s\le 1}|Y_s^{n,\varepsilon }-X_s^0|\\&\quad +\sup _{0\le s\le 1}|H_n(Y_{s-\cdot }^{n,\varepsilon })-H(Y_{s-\cdot }^{n,\varepsilon })|+\mu ([0,\delta ])\sup _{0\le s\le 1}\Vert Y_{s-\cdot }^{n,\varepsilon }-X_{s-\cdot }^0\Vert _\infty \Big \}\\ \xrightarrow {P}&0, \end{aligned}$$

as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty .$ (ii) It is easy to see that

$$\begin{aligned}&\sum _{k=1}^{n}f(X_{t_{k-1}}^\varepsilon ,H_n(X_{t_{k-1}-\cdot }^\varepsilon ),\theta )P_k^i(\theta _0)\\ =&\sum _{k=1}^{n}f(X_{t_{k-1}}^\varepsilon ,H_n(X_{t_{k-1}-\cdot }^\varepsilon ),\theta )\int _{t_{k-1}}^{t_k}\Big (b^i\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\theta _0\big )-b^i\big (X_{t_{k-1}}^\varepsilon ,H_n(X_{t_{k-1}-\cdot }^\varepsilon ),\theta _0\big )\Big )\,\textrm{d}s\\&+\varepsilon \sum _{k=1}^{n}f(X_{t_{k-1}}^\varepsilon ,H_n(X_{t_{k-1}-\cdot }^\varepsilon ),\theta ) \int _{t_{k-1}}^{t_k}\sum _{j=1}^{r}\sigma ^{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _0\big )\,\textrm{d}W_s^j\\ =&\int _{0}^{1}f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta )\Big (b\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\theta _0\big )-b\big (Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta _0\big )\Big )\,\textrm{d}s\\&+\varepsilon \int _{0}^{1}\sum _{j=1}^{r}f(Y_{s}^{n,\varepsilon },H(Y_{s-\cdot }^{n,\varepsilon }),\theta ) \sigma ^{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _0\big )\,\textrm{d}W_s^j. \end{aligned}$$

From the Lipschitz condition on b in (A1) it holds that

$$\begin{aligned}&\sup _{\theta \in \Theta }\bigg |\int _{0}^{1}f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta )\Big (b\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\theta _0\big )-b\big (Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta _0\big )\Big )\,\textrm{d}s\bigg |\\ \le&\int _{0}^{1}\sup _{\theta \in \Theta }\Big |f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta )\Big |\cdot K\Big (\big |X_{s}^\varepsilon -Y_s^{n,\varepsilon }\big |\\&\quad +\big |H_n(Y_{s-\cdot }^{n,\varepsilon })-H(Y_{s-\cdot }^{n,\varepsilon })\big |+\mu ([0,\delta ])\big \Vert X_{s-\cdot }^\varepsilon -Y_{s-\cdot }^{n,\varepsilon }\big \Vert _\infty \Big )\,\textrm{d}s\\ \le&KC\int _{0}^{1}\big (1+|Y_{s}^{n,\varepsilon }|+\mu ([0,\delta ])\Vert Y_{s-\cdot }^{n,\varepsilon }\Vert _\infty \big )^\lambda \Big (\big |X_{s}^\varepsilon -X_s^0\big |+\big |Y_s^{n,\varepsilon }-X_s^0\big |\\&\quad +\big |H_n(Y_{s-\cdot }^{n,\varepsilon })-H(Y_{s-\cdot }^{n,\varepsilon })\big |+\mu ([0,\delta ])\big \Vert X_{s-\cdot }^\varepsilon -X_{s-\cdot }^0\big \Vert +\mu ([0,\delta ])\big \Vert Y_{s-\cdot }^{n,\varepsilon }-X_{s-\cdot }^0\big \Vert \Big )\,\textrm{d}s\\ \le&KC\Big (1+\left( 1+\mu ([0,\delta ])\right) \sup _{-\delta \le s \le 1}\big |X_{s}^\varepsilon \big |\Big )^\lambda \Big \{\sup _{0 \le s \le 1}\big |H_n(Y_{s-\cdot }^{n,\varepsilon })-H(Y_{s-\cdot }^{n,\varepsilon })\big |\\&\quad +\left( 1+\mu ([0,\delta ])\right) (\sup _{-\delta \le s \le 1}\big |X_{s}^\varepsilon -X_s^0\big |+\sup _{-\delta \le s \le 1}\big |Y_s^{n,\varepsilon }-X_s^0\big |)\Big \}, \end{aligned}$$

which converges to zero as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$ by Lemma 2 and Lemma 3. Let $\tau _m^{n,\varepsilon }=\inf \{t\ge 0;|X_t^\varepsilon |\ge m$ or $|Y_t^{n,\varepsilon }|\ge m\}$. We find that $\tau _m^{n,\varepsilon }\rightarrow \infty$  a.s. as $m\rightarrow \infty$ from Lemma 1. Next, we have that for any $\eta >0$,

$$\begin{aligned}&P\Bigg (\varepsilon \sup _{\theta \in \Theta }\bigg |\int _{0}^{1}\sum _{j=1}^{r}f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta ) \sigma ^{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _0\big )\,\textrm{d}W_s^j\bigg |{>2\eta }\Bigg )\nonumber \\ \le&P(\tau _{m}^{n,\varepsilon }<1)+P\Bigg (\varepsilon \sup _{\theta \in \Theta }\bigg |\int _{0}^{1}\sum _{j=1}^{r}f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta ) \sigma ^{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _0\big )\mathbbm {1}_{\{s\le \tau _m^{n,\varepsilon }\}}\,\textrm{d}W_s^j\bigg |{>\eta }\Bigg ). \end{aligned}$$

(5.10)

Let

$$\begin{aligned} u_{n,\varepsilon }^i(\theta )=\varepsilon \int _{0}^{1}\sum _{j=1}^{r}f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta ) \sigma ^{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _0\big )\mathbbm {1}_{\{s\le \tau _m^{n,\varepsilon }\}}\,\textrm{d}W_s^j. \end{aligned}$$

We want to prove that $u_{n,\varepsilon }^i(\theta )\rightarrow 0$ in P as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$, uniformly in $\theta \in \Theta$. Therefore, it is sufficient to check the pointwise convergence and the tightness of the sequence $\{u_{n,\varepsilon }^i(\cdot )\}$. For the pointwise convergence, by Chebyshev’s inequality, the linear growth condition on $\sigma$ in (A1) and itô’s isometry,

$$\begin{aligned} P\left( |u_{n,\varepsilon }^i(\theta )|>\eta \right)&\le \varepsilon ^2\eta ^{-2}E\Bigg [\bigg |\int _{0}^{1}\sum _{j=1}^{r}f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta ) \sigma ^{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _0\big )\mathbbm {1}_{\{s\le \tau _m^{n,\varepsilon }\}}\,\textrm{d}W_s^j\bigg |^2\Bigg ]\nonumber \\&\le \varepsilon ^2\eta ^{-2}\sum _{j=1}^{r}\int _{0}^{1}E\bigg [\Big |f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta ) \sigma ^{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _0\big )\Big |^2\mathbbm {1}_{\{s\le \tau _m^{n,\varepsilon }\}}\bigg ]\,\textrm{d}s\nonumber \\&\le \varepsilon ^2\eta ^{-2}C^2K^2r\Big (1+\big (1+\mu ([0,\delta ])\big )m\Big )^{2(\lambda +1)}. \end{aligned}$$

(5.11)

which converges to zero as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$ with fixed m. For the tightness, by using Theorem 20 in Appendix I of Ibragimov and Has’minskii (1981), it is adequate to prove the following two inequalities:

$$\begin{aligned}&E\left[ \left| u_{n,\varepsilon }^{i}(\theta )\right| ^{2l}\right] \le C, \end{aligned}$$

(5.12)

$$\begin{aligned}&E\left[ \left| u_{n,\varepsilon }^{i}(\theta _2)-u_{n,\varepsilon }^{i}(\theta _1)\right| ^{2l}\right] \le C\left| \theta _2-\theta _1\right| ^{2l}, \end{aligned}$$

(5.13)

for $\theta ,\theta _1,\theta _2\in \Theta$, where $2l>p+q$. The proof of (5.12) is analogous to moment estimates in (5.11) by replacing itô’s isometry with the Burkholder-Davis-Gundy inequality, so we omit the detail here. For (5.13), by using Taylor’s formula and the Burkholder-Davis-Gundy inequality, we get

$$\begin{aligned} E\left[ \left| u_{n,\varepsilon }^{i}(\theta _2)-u_{n,\varepsilon }^{i}(\theta _1)\right| ^{2l}\right]&\le \varepsilon ^{2l}C_lE\Bigg [\bigg (\int _{0}^{1}\sum _{j=1}^{r}\Big |\sigma ^{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _0\big )\Big |^2 \mathbbm {1}_{\{s\le \tau _m^{n,\varepsilon }\}}\times \\&\quad \Big |\big (f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta _2)-f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta _1)\big )\Big |^2\,\textrm{d}s\bigg )^l\Bigg ] \\&\le \varepsilon ^{2l}C_lE\Bigg [\bigg (\int _{0}^{1}\int _0^1\sum _{j=1}^{r}\Big |\sigma ^{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ),\beta _0\big )\Big |^2 \mathbbm {1}_{\{s\le \tau _m^{n,\varepsilon }\}}\times \\&\quad \Big |\theta _2-\theta _1\Big |^2\Big |\triangledown _{\theta }f\left( Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta _1+v(\theta _2-\theta _1)\right) \Big |^2\,\textrm{d}vds\bigg )^l\Bigg ]\\&\le \varepsilon ^{2l}C_lC^{2l}K^{2l}r^{l}\Big (1+\big (1+\mu ([0,\delta ])\big )m\Big )^{(2\lambda +2) l}\big |\theta _2-\theta _1\big |^{2l}. \end{aligned}$$

Combining (5.10) and arguments above, we have that

$$\begin{aligned} \varepsilon \sup _{\theta \in \Theta }\bigg |\int _{0}^{1}\sum _{j=1}^{r}f(Y_{s}^{n,\varepsilon },H_n(Y_{s-\cdot }^{n,\varepsilon }),\theta ) \sigma ^{ij}\big (X_{s}^\varepsilon ,H(X_{s-\cdot }^\varepsilon ,\beta _0\big )\,\textrm{d}W_s^j\bigg |, \end{aligned}$$

converges to zero in probability as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$. Therefore, the proof is complete. $\square$

In Lemma 8, the proof ideas follow Sørensen and Uchida (2003).

Lemma 8

Let $f\in C_{\uparrow }^{1,1,1}({\mathbb {R}}^d\times {\mathbb {R}}^d\times \Theta )$ and suppose the conditions (A1)–(A3). If $(\sqrt{n}\varepsilon )^{-1}\rightarrow 0$ as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$, then the following (i) and (ii) hold true:

• (i) As $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$,

  $$\begin{aligned}&\varepsilon ^{-2} \sum _{k=1}^{n} f\left( X_{t_{k-1}}^\varepsilon , H_n\big (X_{t_{k-1}-\cdot }^\varepsilon \big ), \theta \right) P_{k}^{i}(\theta _{0}) P_{k}^{j}(\theta _{0})\\&\xrightarrow {P} \int _{0}^{1} f\left( X_{s}^0, H\big (X_{s - \cdot }^0\big ), \theta \right) \left[ \sigma \sigma ^{\top }\right] ^{ij}\left( X_{s}^0, H\big (X_{s - \cdot }^0\big ),\beta _{0}\right) \,\textrm{d}s, \end{aligned}$$

  uniformly in $\theta \in \Theta .$

• (ii) As $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$,

  $$\begin{aligned}&\varepsilon ^{-2} \sum _{k=1}^{n} f\left( X_{t_{k-1}}^\varepsilon , H_n\big (X_{t_{k-1} - \cdot }^\varepsilon \big ), \theta \right) P_{k}^{i}(\theta ) P_{k}^{j}(\theta )\\ \xrightarrow {P}&\int _{0}^{1} f\left( X_{s}^0, H\big (X_{s - \cdot }^0\big ), \theta \right) \left[ \sigma \sigma ^{\top }\right] ^{ij}\left( X_{s}^0, H\big (X_{s - \cdot }^0\big ),\beta _{0}\right) \,\textrm{d}s, \end{aligned}$$

  uniformly in $\theta \in \Theta .$

Proof

(i) It holds from Lemma 6, Lemma 7(i), and the Hölder’s inequality that

$$\begin{aligned} \sum _{k=1}^{n}E&\left[ \varepsilon ^{-2} f\left( X_{t_{k-1}}, H_n\big (X_{t_{k-1}-\cdot }\big ), \theta \right) P_{k}^{i}(\theta _{0}) P_{k}^{j}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right] \\ \xrightarrow {P}&\int _{0}^{1} f\left( X_{s}^0, H\big (X_{s - \cdot }^0\big ), \theta \right) \left[ \sigma \sigma ^{\top }\right] ^{ij}\left( X_{s}^0, H\big (X_{s - \cdot }^0\big ), \beta _{0}\right) \,\textrm{d}s, \end{aligned}$$

$$\begin{aligned} \sum _{k=1}^{n}E\left[ \varepsilon ^{-4} f\left( X_{t_{k-1}}, H_n\big (X_{t_{k-1}-\cdot }\big ), \theta \right) ^2 \left( P_{k}^{i}(\theta _{0}) P_{k}^{j}(\theta _{0})\right) ^2\bigg |{\mathscr {F}}_{t_{k-1}}\right] \xrightarrow {P} 0, \end{aligned}$$

as $n \rightarrow \infty$ and $\varepsilon \rightarrow 0$. Therefore, it follows from Lemma 9 in Genon-Catalot and Jacod (1993)

$$\begin{aligned}&\varepsilon ^{-2} \sum _{k=1}^{n} f\left( X_{t_{k-1}}, H_n(X_{t_{k-1}-\cdot }), \theta \right) P_{k}^{i}(\theta _{0}) P_{k}^{j}(\theta _{0})\\ \xrightarrow {P}&\int _{0}^{1} f\left( X_{s}^0, H(X_{s - \cdot }^0), \theta \right) [\sigma \sigma ^{\top }]^{ij}\left( X_{s}^0, H(X_{s - \cdot }^0),\beta _{0}\right) \,\textrm{d}s, \end{aligned}$$

as $n \rightarrow \infty$ and $\varepsilon \rightarrow 0$. For the tightness of the sequence $\{\varepsilon ^{-2}\sum _{k=1}^{n}f\left( X_{t_{k-1}},H_n(X_{t_{k-1}}),\cdot \right) P_k^iP_k^j(\theta _0)\}$, according to Lemma 6,

$$\begin{aligned}&\sup _{n,\varepsilon }E\Bigg [\sup _{\theta }\bigg |\varepsilon ^{-2} \sum _{k=1}^n\frac{\partial }{\partial \theta }f\left( X_{t_{k-1}},H_n(X_{t_{k-1}}),\theta \right) P_{k}^{i}(\theta _{0}) P_{k}^{j}(\theta _{0})\bigg |\Bigg ]\\ \le&\sup _{n,\varepsilon }E\Bigg [\frac{\varepsilon ^{-2}}{2} \sum _{k=1}^n\sup _{\theta }\bigg |\frac{\partial }{\partial \theta }f\left( X_{t_{k-1}},H_n(X_{t_{k-1}}),\theta \right) \bigg | E\Big [\big (P_{k}^{i}(\theta _{0})\big )^2+ \big (P_{k}^{j}(\theta _{0})\big )^2\Big |{\mathscr {F}}_{t_{k-1}}\Big ]\Bigg ]\\ \le&\frac{1}{2}\sup _{n,\varepsilon }E\Bigg [\sum _{k=1}^n\sup _{\theta }\bigg |\frac{\partial }{\partial \theta }f\left( X_{t_{k-1}},H_n(X_{t_{k-1}}),\theta \right) \bigg |\times \\&\quad \bigg \{\frac{1}{n}([\sigma \sigma ^{\top }]_{t_{k-1},H}^{ii}+[\sigma \sigma ^{\top }]_{t_{k-1},H}^{jj})+\frac{1}{n^2\varepsilon ^2}\left( b_{t_{k-1},H}^{i_1}-b_{t_{k-1},H_n}^{i_1}\right) \left( b_{t_{k-1},H}^{i_2}-b_{t_{k-1},H_n}^{i_2}\right) \\&\qquad +\int _{t_{k-1}}^{t_k}\left\{ 4\varepsilon ^{-2}\Phi _2^\varepsilon (s)+\Phi _1^\varepsilon (s)\right\} ~ds\\&\qquad +R_{k-1}^{{\varepsilon }}(\varepsilon ^{-2})\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s}\Phi _1^\varepsilon (u)\,\textrm{d}u\,\textrm{d}s+R_{k-1}^{{\varepsilon }}\left( \frac{1}{n\varepsilon ^2}\right) \int _{t_{k-1}}^{t_k}\Phi _1^\varepsilon (s)\,\textrm{d}s\\&\qquad +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^3\varepsilon ^2}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon ^{-1}}{n^2\sqrt{n}}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{1}{n^2}\right) +R_{k-1}^{{\varepsilon }}\left( \frac{\varepsilon }{n\sqrt{n}}\right) \bigg \}\Bigg ] <\infty . \end{aligned}$$

(ii) Noticing that

$$\begin{aligned} P_k^iP_k^j(\theta )&=P_k^iP_k^j(\theta _0)+\frac{1}{n}P_k^i(\theta _0)B^j_{k-1}(\theta _0,\theta )+\frac{1}{n}P_k^j(\theta _0)B^i_{k-1}(\theta _0,\theta )+\frac{1}{n^2}B^i_{k-1}B^j_{k-1}(\theta _0,\theta ), \end{aligned}$$

where $B^i_{k-1}(\theta _0,\theta )=b^i\left( X_{t_{k-1}},H_n(X_{t_{k-1}-\cdot }),\theta _0\right) -b^i\left( X_{t_{k-1}},H_n(X_{t_{k-1}-\cdot }),\theta \right)$. It follows from Lemmas 7 and 8(i), under P, as $n\rightarrow \infty$ and $\varepsilon \rightarrow 0$,

$$\begin{aligned}&\varepsilon ^{-2} \sum _{k=1}^{n} f\left( X_{t_{k-1}}, H_n(X_{t_{k-1}-\cdot }), \theta \right) P_{k}^{i}P_{k}^{j}(\theta )\\&= \varepsilon ^{-2} \sum _{k=1}^{n} f\left( X_{t_{k-1}}, H_n(X_{t_{k-1}-\cdot }), \theta \right) P_k^iP_k^j(\theta _0)\\&\quad +\frac{\varepsilon ^{-2}}{n^2}\sum _{k=1}^{n} f\left( X_{t_{k-1}}, H_n(X_{t_{k-1}-\cdot }), \theta \right) B^i_{k-1}B^j_{k-1}(\theta _0,\theta )\\&\quad +\frac{1}{n\varepsilon ^2}\sum _{k=1}^{n} \bigg [f\left( X_{t_{k-1}}, H_n(X_{t_{k-1}-\cdot }), \theta \right) \times \\&\qquad \Big \{P_k^i(\theta _0)B^j_{k-1}(\theta _0,\theta )+P_k^j(\theta _0)B^i_{t_{k-1}}(\theta _0,\theta )\Big \}\bigg ]\\&\rightarrow \int _{0}^{1} f\left( X_{s}^0, H(X_{s - \cdot }^0), \theta \right) [\sigma \sigma ^{\top }]^{ij}\left( X_{s}^0, H(X_{s - \cdot }^0),\beta _{0}\right) \,\textrm{d}s, \end{aligned}$$

uniformly in $\theta \in \Theta$. $\square$

We are ready to prove Theorem 1. In Theorem 1, the proof ideas mainly follow Sørensen and Uchida (2003).

Proof of Theorem 1

Following the proof of Theorem 1 in Sørensen and Uchida (2003), the consistency follows from the two properties:

$$\begin{aligned}&\varepsilon ^{2} \{U_{n,\varepsilon }(\alpha , \beta )-U_{n,\varepsilon }(\alpha _0, \beta )\} \xrightarrow {P} \int _{0}^{1} B_s^{\top }(\theta _0, \theta ) [\sigma \sigma ^{\top }]^{-1}(X_{s}^0, H(X_{s - \cdot }^0),\beta _{0})B_s(\theta _0, \theta )\,\textrm{d}s, \end{aligned}$$

(5.14)

$$\begin{aligned}&\frac{1}{n}U_{n,\varepsilon }(\alpha ,\beta )\xrightarrow {P}\int _0^1\log \det [\sigma \sigma ^{\top }]\Bigl (X_{s}^0,H(X_{s-\cdot }^0),\beta \Bigr )\,\textrm{d}s\nonumber \\&\quad +\int _0^1\textrm{tr}\bigg [[\sigma \sigma ^{\top }]\Bigl (X_{s},H(X_{s-\cdot }),\beta \Bigr )[\sigma \sigma ^{\top }]^{-1}\Bigl (X_{s},H(X_{s-\cdot }),\beta _{0}\Bigr )\bigg ]\,\textrm{d}s, \end{aligned}$$

(5.15)

where $B_s(\theta _0, \theta )=b\left( X_s^0,H(X_{s-\cdot }^0),\theta _0\right) -b\left( X_s^0,H(X_{s-\cdot }^0),\theta \right)$, as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty ,$ uniformly in $\theta \in \Theta .$ First, we show (5.14). It is clear that

$$\begin{aligned}&\varepsilon ^{2} \{U_{n,\varepsilon }(\alpha , \beta )-U_{n,\varepsilon }(\alpha _0, \beta )\}\\&= n\sum _{k=1}^{n}\big (P_k(\theta )-P_k(\theta _0)\big )^{\top }\Xi _{k-1}^{-1}(\beta )\big (P_k(\theta )+P_k(\theta _0)\big )\\&= \sum _{k=1}^{n}\bigg [\Big (b\left( X_{t_{k-1}},H_n(X_{t_{k-1}-\cdot }),\theta _0\right) -b\left( X_{t_{k-1}},H_n(X_{t_{k-1}-\cdot }),\theta \right) \Big )^{\top }\\&\quad \Xi _{k-1}^{-1}(\beta )\bigg \{2\Big (\Delta _k X-\frac{1}{n}b\left( X_{t_{k-1}},H_n(X_{t_{k-1}-\cdot }),\theta _0\right) \Big )\\&\quad +\frac{1}{n}\Big (b\left( X_{t_{k-1}},H_n(X_{t_{k-1}-\cdot }),\theta _0\right) -b\left( X_{t_{k-1}},H_n(X_{t_{k-1}-\cdot }),\theta \right) \Big )\bigg \}\bigg ]. \end{aligned}$$

From Lemma 7,

$$\begin{aligned} \varepsilon ^{2} \{U_{n,\varepsilon }(\alpha , \beta )-U_{n,\varepsilon }(\alpha _0, \beta )\} \xrightarrow {P} \int _{0}^{1} B_s^{\top }(\theta _0, \theta ) [\sigma \sigma ^{\top }]^{-1}(X_{s}^0, H(X_{s - \cdot }^0),\beta _{0})B_s(\theta _0, \theta )\,\textrm{d}s, \end{aligned}$$

as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty ,$ uniformly in $\theta \in \Theta .$ About (5.15), from Lemma 7(i) and Lemma 8(ii), as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty ,$ it holds that

$$\begin{aligned} \frac{1}{n}U_{n,\varepsilon }(\alpha ,\beta )\xrightarrow {P}&\int _0^1\log \det [\sigma \sigma ^{\top }]\Bigl (X_{s}^0,H(X_{s-\cdot }^0),\beta \Bigr )\,\textrm{d}s\\&\quad +\int _0^1\textrm{tr}\bigg [[\sigma \sigma ^{\top }]\Bigl (X_{s},H(X_{s-\cdot }),\beta \Bigr )[\sigma \sigma ^{\top }]^{-1}\Bigl (X_{s},H(X_{s-\cdot }),\beta _{0}\Bigr )\bigg ]\,\textrm{d}s. \end{aligned}$$

$\square$

Finally, we prove the asymptotic normality of $\widehat{\theta }_{n,\varepsilon }$. For the proof, we shall use the notations:

• (N14) We denote

  $$\begin{aligned} \Lambda _{n,\varepsilon }(\theta _0):= \left( \begin{array}{cc} -\varepsilon \left( \frac{\partial }{\partial \alpha _i}U_{n,\varepsilon }(\theta )\Big |_{\theta =\theta _0}\right) _{1\le i\le p} \\ -\frac{1}{\sqrt{n}}\left( \frac{\partial }{\partial \beta _i}U_{n,\varepsilon }(\theta )\Big |_{\theta =\theta _0}\right) _{1\le i\le q} \\ \end{array} \right) . \end{aligned}$$

• (N15) We denote

  $$\begin{aligned} C_{n,\varepsilon }(\theta _0):= \left( \begin{array}{cc} \varepsilon ^2\left( \frac{\partial ^2}{\partial \alpha _i\alpha _j}U_{n,\varepsilon }(\theta )\Big |_{\theta =\theta _0}\right) _{1\le i,j\le p} &{}\frac{\varepsilon }{\sqrt{n}}\left( \frac{\partial ^2}{\partial \alpha _i\beta _j}U_{n,\varepsilon }(\theta )\Big |_{\theta =\theta _0}\right) _{1\le i\le p,1\le j\le q}\\ \frac{\varepsilon }{\sqrt{n}}\left( \frac{\partial ^2}{\partial \beta _i\alpha _j}U_{n,\varepsilon }(\theta )\Big |_{\theta =\theta _0}\right) _{1\le i\le p,1\le j\le q}&{}\frac{1}{n}\left( \frac{\partial ^2}{\partial \beta _i\beta _j}U_{n,\varepsilon }(\theta )\Big |_{\theta =\theta _0}\right) _{1\le i,j\le q} \\ \end{array} \right) . \end{aligned}$$

In Theorem 2, the proof ideas mainly follow Sørensen and Uchida (2003).

Proof of Theorem 2

By Theorem 1 in Sørensen and Uchida (2003), the asymptotic normality follows from the three properties:

$$\begin{aligned} C_{n,\varepsilon }(\theta _0)\xrightarrow {P}2I(\theta _0), \end{aligned}$$

(5.16)

$$\begin{aligned} \sup _{|\theta |\le \eta _{n,\varepsilon }}|C_{n,\varepsilon }(\theta _0+\theta )-C_{n,\varepsilon }(\theta _0)|\xrightarrow {P}0, \end{aligned}$$

(5.17)

where $\eta _{n,\varepsilon }\rightarrow 0$, as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$, and

$$\begin{aligned} \Lambda _{n,\varepsilon }(\theta _0)\xrightarrow {d} N(0,4I(\theta _{0})), \end{aligned}$$

(5.18)

as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$. First, we show (5.16). Note that

$$\begin{aligned} \varepsilon ^2\frac{\partial ^2}{\partial \alpha _i\partial \alpha _j}U_{n,\varepsilon }(\theta )&= -2\sum _{k=1}^{n}\Bigg [\bigg (\frac{\partial ^2}{\partial \alpha _i\partial \alpha _j}b_{t_{k-1},H_n}(\theta )\bigg )^{\top }\Xi _{k-1}^{-1}(\beta )\nonumber \\&\quad \Big \{P_k(\theta _0)+\frac{1}{n}\Big (b_{t_{k-1},H_n}(\theta _0)-b_{t_{k-1},H_n}(\theta )\Big )\Big \}\Bigg ]\nonumber \\&\quad +\frac{2}{n}\sum _{k=1}^{n}\bigg (\frac{\partial }{\partial \alpha _i}b_{t_{k-1},H_n}(\theta )\bigg )^{\top }\Xi _{k-1}^{-1}(\beta )\bigg (\frac{\partial }{\partial \alpha _j}b_{t_{k-1},H_n}(\theta )\bigg ), \end{aligned}$$

(5.19)

$$\begin{aligned}&\frac{\varepsilon }{\sqrt{n}}\frac{\partial ^2}{\partial \alpha _i\partial \beta _j}U_{n,\varepsilon }(\theta )\nonumber \\ =&\frac{-2}{\varepsilon \sqrt{n}}\sum _{k=1}^{n}\Bigg \{\bigg (\frac{\partial ^2}{\partial \alpha _i\partial \beta _j}b_{t_{k-1},H_n}(\theta )\bigg )^{\top }\Xi _{k-1}^{-1}(\beta )+\bigg (\frac{\partial }{\partial \alpha _i}b_{t_{k-1},H_n}(\theta )\bigg )^{\top }\bigg (\frac{\partial }{\partial \beta _j}\Xi _{k-1}^{-1}(\beta )\bigg )\Bigg \}\nonumber \\&\quad \cdot \Big \{P_k(\theta _0)+\frac{1}{n}\Big (b_{t_{k-1},H_n}(\theta _0)-b_{t_{k-1},H_n}(\theta )\Big )\Big \}\nonumber \\&+\frac{2}{\varepsilon n\sqrt{n}}\sum _{k=1}^{n}\bigg (\frac{\partial }{\partial \alpha _i}b_{t_{k-1},H_n}(\theta )\bigg )^{\top }\Xi _{k-1}^{-1}(\beta )\bigg (\frac{\partial }{\partial \beta _j}b_{t_{k-1},H_n}(\theta )\bigg ), \end{aligned}$$

(5.20)

$$\begin{aligned}&\frac{1}{n}\frac{\partial ^2}{\partial \beta _i\partial \beta _j}U_{n,\varepsilon }(\theta )\nonumber \\ =&\frac{1}{n}\sum _{k=1}^{n}\frac{\partial ^2}{\partial \beta _i\partial \beta _j}\log \det \Xi _{k-1}(\beta ) -\frac{2\varepsilon ^{-1}}{n}\sum _{k=1}^{n}\Bigg \{\bigg (\frac{\partial ^2}{\partial \beta _i\partial \beta _j}b_{t_{k-1},H_n}(\theta )\bigg )^{\top }\Xi _{k-1}^{-1}(\beta )\nonumber \\&\quad +\bigg (\frac{\partial }{\partial \beta _i}b_{t_{k-1},H_n}(\theta )\bigg )^{\top }\bigg (\frac{\partial }{\partial \beta _j}\Xi _{k-1}^{-1}(\beta )\bigg ) +\bigg (\frac{\partial }{\partial \beta _j}b_{t_{k-1},H_n}(\theta )\bigg )^{\top }\bigg (\frac{\partial }{\partial \beta _i}\Xi _{k-1}^{-1}(\beta )\bigg )\Bigg \}\nonumber \\&\quad \cdot \Big \{P_k(\theta _0)+\frac{1}{n}\Big (b_{t_{k-1},H_n}(\theta _0)-b_{t_{k-1},H_n}(\theta )\Big )\Big \}\nonumber \\ +&\frac{2\varepsilon ^{-1}}{n^2}\sum _{k=1}^{n}\bigg (\frac{\partial }{\partial \beta _i}b_{t_{k-1},H_n}(\theta )\bigg )^{\top }\Xi _{k-1}^{-1}(\beta )\bigg (\frac{\partial }{\partial \beta _j}b_{t_{k-1},H_n}(\theta )\bigg )\nonumber \\ +&\varepsilon ^{-2}\sum _{k=1}^{n}\big (P_k(\theta )\big )^{\top }\bigg (\frac{\partial ^2}{\partial \beta _i\partial \beta _j}\Xi _{k-1}^{-1}(\beta )\bigg )P_k(\theta ). \end{aligned}$$

(5.21)

It follows from Lemma 7 and Lemma 8(ii), as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty ,$ that

$$\begin{aligned}&\varepsilon ^2\frac{\partial ^2}{\partial \alpha _i\partial \alpha _j}U_{n,\varepsilon }(\theta )&\\ \xrightarrow {P}&2\int _0^1\bigg (\frac{\partial }{\partial \alpha _i}b\left( X_{s}^0,H(X_{s-\cdot }^0),\theta \right) \bigg )^{\top }\left[ \sigma \sigma ^{\top }\right] ^{-1}\left( X_s^0,H(X_{s-\cdot }^0),\beta \right) \bigg (\frac{\partial }{\partial \alpha _j}b\left( X_{s}^0,H(X_{s-\cdot }^0),\theta \right) \bigg )\,\textrm{d}s&\\&-2\int _0^1\bigg (\frac{\partial ^2}{\partial \alpha _i\partial \alpha _j}b(X_{s}^0,H(X_{s-\cdot }^0),\theta )\bigg )^{\top }\left[ \sigma \sigma ^{\top }\right] ^{-1}\left( X_s^0,H(X_{s-\cdot }^0),\beta \right) B\left( X_s^0, \theta _0, \theta \right) \,\textrm{d}s,&\\&\frac{\varepsilon }{\sqrt{n}}\frac{\partial ^2}{\partial \alpha _i\partial \beta _j}U_{n,\varepsilon }(\theta )\xrightarrow {P}0,&\\&\frac{1}{n}\frac{\partial ^2}{\partial \beta _i\partial \beta _j}U_{n,\varepsilon }(\theta )&\\ \xrightarrow {P}&\int _0^1\frac{\partial ^2}{\partial \beta _i\partial \beta _j}\log \det \left[ \sigma \sigma ^{\top }\right] \left( X_s^0,H(X_{s-\cdot }^0),\beta \right) \,\textrm{d}s&\\&+\int _0^1\textrm{tr}\Bigg [\left[ \sigma \sigma ^{\top }\right] \left( X_s^0,H(X_{s-\cdot }^0),\beta \right) \bigg (\frac{\partial ^2}{\partial \beta _i\partial \beta _j}\left[ \sigma \sigma ^{\top }\right] ^{-1}\left( X_s^0,H(X_{s-\cdot }^0),\beta \right) \bigg )\Bigg ]\,\textrm{d}s,&\end{aligned}$$

uniformly in $\theta \in \Theta$. About (5.17), the limit of (5.19), (5.20) and (5.21) are continuous with respect to $\theta$, which completes the proof. Finally, we prove (5.18). We set

$$\begin{aligned} -\varepsilon \frac{\partial }{\partial \alpha _{i}}U_{n,\varepsilon }(\theta )\bigg |_{\theta =\theta _{0}}&= \sum _{k=1}^{n}2\varepsilon ^{-1}\left( \frac{\partial }{\partial \alpha _{i}}b_{t_{k-1},H_n}\bigl (\theta _0\bigr )\right) ^{\top }\Xi _{k-1}^{-1}(\beta _0)P_{k}(\theta _0)\\&=:\sum _{k=1}^{n}\xi _{k}^{i}(\theta _{0}), \\ -\frac{1}{\sqrt{n}}\frac{\partial }{\partial \beta _{i}}U_{n,\varepsilon }(\theta )\bigg |_{\theta =\theta _{0}}&= -\sum _{k=1}^{n}\frac{1}{\sqrt{n}}\frac{\partial }{\partial \beta _{i}}\log \det \Xi _{k-1}(\beta _0)\\&\quad -\sum _{k=1}^{n}\sqrt{n}\varepsilon ^{-2}\Bigl (P_{k}(\theta _{0})\Bigr )^{\top }\left( \frac{\partial }{\partial \beta _{i}}\Xi _{k-1}^{-1}(\beta _0)\right) P_{k}(\theta _{0})\\&\quad +2\sum _{k=1}^{n}\frac{\varepsilon ^{-2}}{\sqrt{n}}\left( \frac{\partial }{\partial \beta _{i}}b_{t_{k-1},H_n}\bigl (\theta _{0}\bigr )\right) ^{\top }\Xi _{k-1}^{-1}(\beta _0)P_{k}(\theta _{0})\\&=:\sum _{k=1}^{n}\eta _{k}^{i}(\theta _{0}). \end{aligned}$$

In view of Theorem 3.2 and 3.4 in Hall and Heyde (1980), it is sufficient to show that as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$,

$$\begin{aligned}&\sum _{k=1}^{n}E\left[ \xi _{k}^{i}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right] \xrightarrow {P}0, \end{aligned}$$

(5.22)

$$\begin{aligned}&\sum _{k=1}^{n}E\left[ \eta _{k}^{j}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right] \xrightarrow {P}0, \end{aligned}$$

(5.23)

$$\begin{aligned}&\sum _{k=1}^{n}E\left[ \xi _{k}^{i_{1}}(\theta _{0})\xi _{k}^{i_{2}}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right] \xrightarrow {P}4I_{b}^{i_{1}i_{2}}(\theta _{0}),\end{aligned}$$

(5.24)

$$\begin{aligned}&\sum _{k=1}^{n}E\left[ \eta _{k}^{j_{1}}(\theta _{0})\eta _{k}^{j_{2}}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right] \xrightarrow {P}4I_{\sigma }^{j_{1}j_{2}}(\theta _{0}),\end{aligned}$$

(5.25)

$$\begin{aligned}&\sum _{k=1}^{n}E\left[ \xi _{k}^{i}(\theta _{0})\eta _{k}^{j}(\theta _{0})\Big |{\mathscr {F}}_{t_{k-1}}\right] \xrightarrow {P}0,\end{aligned}$$

(5.26)

$$\begin{aligned}&\sum _{k=1}^{n}E\left[ (\xi _{k}^{i}(\theta _{0}))^{4}\Big |{\mathscr {F}}_{t_{k-1}}\right] \xrightarrow {P}0, \end{aligned}$$

(5.27)

$$\begin{aligned}&\sum _{k=1}^{n}E\left[ (\eta _{k}^{j}(\theta _{0}))^{4}\Big |{\mathscr {F}}_{t_{k-1}}\right] \xrightarrow {P}0. \end{aligned}$$

(5.28)

From Lemma 6, we obtain (5.22–5.27). To prove (5.28), we have several estimates as follows:

$$\begin{aligned}&\big (\eta _{k}^{j}(\theta _{0})\big )^4\nonumber \\ \le&3^3\Bigg \{\frac{1}{n^2}\bigg (\frac{\partial }{\partial \beta _{j}}\log \det \Xi _{k-1}(\beta _0)\bigg )^4+n^2\varepsilon ^{-8}(2d)^3\sum _{l_1,l_2}^{d} \Bigg [\bigg (\frac{\partial }{\partial \beta _j}\Xi _{k-1}^{-1}(\beta _0)\bigg )^{l_1l_2}\Bigg ] ^4\big (P_k^{l_1}P_k^{l_2}(\theta _0)\big )^4\nonumber \\&+16n^{-2}\varepsilon ^{-8}d^3\sum _{l_1}^{d}\Bigg [\bigg \{\biggl (\frac{\partial }{\partial \beta _{j}}b_{t_{k-1}, H_n}\bigl (\theta _{0}\bigr )\biggr )^{\top }\Xi _{k-1}^{-1}(\beta _0)\bigg \}^{l_1}\Bigg ]^4 \big (P_{k}^{l_1}(\theta _{0})\big )^4\Bigg \}, \end{aligned}$$

(5.29)

$$\begin{aligned}&E\Big [\big (P_k^{l_1}P_k^{l_2}(\theta _0)\big )^4\Big |{\mathscr {F}}_{t_{k-1}}\Big ]\le 3^3\bigg \{E\Big [\Big (\big (\Delta _k X\big )^{l_1}\big (\Delta _k X\big )^{l_2}\Big )^4\Big |{\mathscr {F}}_{t_{k-1}}\Big ]\nonumber \\&\quad +\frac{1}{n^4}\Big (b_{t_{k-1}, H_n}^{l_1}\big (\theta _{0}\big )\Big )^4E\Big [\Big (\big (\Delta _k X\big )^{l_2}\Big )^4\Big |{\mathscr {F}}_{t_{k-1}}\Big ]\nonumber \\&\quad +\frac{1}{n^4}\Big (b_{t_{k-1}, H_n}^{l_2}\big (\theta _{0}\big )\Big )^4E\Big [\big (P_k^{l_1}(\theta _0)\big )^4\Big |{\mathscr {F}}_{t_{k-1}}\Big ] \bigg \}. \end{aligned}$$

(5.30)

In the same way as the proof of Lemma 6, we have

$$\begin{aligned}&E\bigg [\prod _{i=1}^{8}\Big (\Delta _k X^{\varepsilon }\Big )^{l_i}\bigg |{\mathscr {F}}_{t_{k-1}}\bigg ]\nonumber \\&= R_{k-1}^{{\varepsilon }}\bigg (\frac{1}{n^8}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^2}{n^7}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^4}{n^6}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^6}{n^5}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^8}{n^4}\bigg )\nonumber \\&+\int _{t_{k-1}}^{t_k}\{\Phi _8^\varepsilon (s_1)+\varepsilon ^2\Phi _7^\varepsilon (s_1)\}\,\textrm{d}s_1\nonumber \\&+\sum _{i=1}^{6}\sum _{j=0}^{6-i}R_{k-1}^{{\varepsilon }}(\varepsilon ^{2j})\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s_1}\cdots \int _{t_{k-1}}^{s_i}\{\Phi _{8-i-j}^\varepsilon (s_{i+1})+\varepsilon ^2\Phi _{7-i-j}^\varepsilon (s_{i+1})\}\,\textrm{d}s_{i+1}\cdots \,\textrm{d}s_1\nonumber \\&+R_{k-1}^{{\varepsilon }}(1)\int _{t_{k-1}}^{t_k}\int _{t_{k-1}}^{s_1}\cdots \int _{t_{k-1}}^{s_7}\Phi _1^\varepsilon (s_8)\,\textrm{d}s_8\cdots \,\textrm{d}s_1\nonumber \\&+R_{k-1}^{{\varepsilon }}\bigg (\frac{1}{n^9}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon }{n^8\sqrt{n}}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^2}{n^8}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^3}{n^7\sqrt{n}}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^4}{n^7}\bigg )\nonumber \\&+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^5}{n^6\sqrt{n}}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^6}{n^6}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^7}{n^5\sqrt{n}}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^8}{n^5}\bigg )+R_{k-1}^{{\varepsilon }}\bigg (\frac{\varepsilon ^9}{n^4\sqrt{n}}\bigg ). \end{aligned}$$

(5.31)

It follows from Lemma 6, (5.29–5.31) and the Hölder’s inequality that

$$\begin{aligned} \sum _{k=1}^{n}E\left[ (\eta _{k}^{j}(\theta _{0}))^{4}\Big |{\mathscr {F}}_{t_{k-1}}\right] \xrightarrow {P} 0, \end{aligned}$$

as $\varepsilon \rightarrow 0$ and $n\rightarrow \infty$. We obtain the conclusion. $\square$