A buyer’s guide to the Hubble constant

Abstract

Since the expansion of the universe was first established by Edwin Hubble and Georges Lemaître about a century ago, the Hubble constant $H_0$ which measures its rate has been of great interest to astronomers. Besides being interesting in its own right, few properties of the universe can be deduced without it. In the last decade, a significant gap has emerged between different methods of measuring it, some anchored in the nearby universe, others at cosmological distances. The SH0ES team has found $H_0 = 73.2 \pm 1.3 \; \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ locally, whereas the value found for the early universe by the Planck Collaboration is $H_0 = 67.4 \pm 0.5 \; \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ from measurements of the cosmic microwave background. Is this gap a sign that the well-established ${\varLambda} {\text{CDM}}$ cosmological model is somehow incomplete? Or are there unknown systematics? And more practically, how should humble astronomers pick between competing claims if they need to assume a value for a certain purpose? In this article, we review results and what changes to the cosmological model could be needed to accommodate them all. For astronomers in a hurry, we provide a buyer’s guide to the results, and make recommendations.

1 Introduction

In 1917, Einstein was the first to combine the assumptions of homogeneity and isotropy with his new theory of general relativity, and produce a solution for the universe as a whole (Einstein 1917). Einstein imposed his belief in a static universe, and famously introduced the cosmological constant $\varLambda$, to make his equations compatible with this assumption. Friedmann (1922) derived a solution for an expanding (or contracting) universe, but his work remained largely unknown until after his death. Establishing expansion as an observational fact was very challenging with the technology of the day. George Lemaître published the first estimate of the expansion rate in Lemaître (1927). Two years later, Edwin Hubble¹ combined his observations of stellar magnitudes using the Mount Wilson telescope with Shapley’s, Humanson’s and Slipher’s redshifts z to a similar result (Hubble 1929) (Fig. 1). Hubble’s constant, as it later became known, is then the constant of proportionality between recession speed v and distance d:

$$\begin{aligned} v = H_0 \, d \;. \end{aligned}$$

(1)

Fig. 1

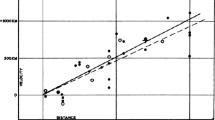
Hubble’s original diagram from Hubble (1929). Despite the typo on the labelling of the y-axis, which should read $\hbox {kms}^{-1}$ and not $\hbox {km}$, it is still easy to read off $H_0 \simeq 500\; \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. Hubble and Humanson were using the largest telescope in the world at the time. M31 is recognisable as the lowest black dot in the bottom left; Humanson had determined it is velocity as $220 \;\hbox {kms}^{-1}$ towards the Milky Way (the modern value is $110 \;\hbox {kms}^{-1}$)

Surprisingly perhaps, it was not until 1958 that the first recognisably modern value $H_0 \simeq 75 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ was published (Sandage 1958). Sandage made several corrections to Hubble’s earlier results. First, he noted the population of Cepheid variable stars was not as homogeneous as first thought. This added both scatter and bias to distance estimates, compounded by the low numbers of Cepheids observed. Second, and more seriously, Hubble had mistaken (far brighter) HII regions as bright stars, and, therefore, his estimate of the distances to galaxies was too low.

Fast forward to today, and these historical developments seem to echo some present day debates. $H_0$ is measured in a number of ways, which produce inconsistent values. In particular, in 2018, the Planck Collaboration used the Cosmic Microwave Background (CMB) temperature and polarization anisotropies and the ${\varLambda} {\text{CDM}}$ cosmological model, to find $H_0 = 67.4 \pm 0.5 \; \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Planck Collaboration 2020) whereas in 2021 the SH0ES Collaboration (Riess et al. 2021) used Cepheids and supernovae to find $H_0 = 73.2 \pm 1.3 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (here, and for the rest of the review we quote 68% confidence limits). We show the main modern results in Fig. 2.

Why should this disagreement matter? First, it may be a sign that the standard cosmological model is incomplete and new physics is required. All $H_0$ results place some reliance on a background cosmology (for example to obtain peculiar velocity adjustments from a model), but the sensitivity is large when comparing results projected over large distances. Second, other cosmological parameters such as matter densities, curvature and large scale structure are often degenerate with $H_0$ in observational data; knowing $H_0$ more accurately helps resolve their values too. Third, knowing $H_0$ accurately improves astrophysics, as distances in the universe are $\propto H_0^{-1}$. Its dimensionless cousin $h = H_0 / 100 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ is ubiquitous in formulae.

We organise our review as follows. Section 1 defines $H_0$ and distances; it may be skipped by a reader familiar with cosmological models. In Sect. 2, we show how $H_0$ is calculated from observational data, and the type of problems that might generally arise. We also briefly discuss the use of Bayesian methods as a tool to discriminate between competing observations and models. In Sect. 3, we discuss ways in which $H_0$ has been recently estimated. There is a rich literature on the subject, and it is difficult to cover all papers. Our approach is to cite for each topic a seminal paper, and the recent most significant developments. In Sect. 4, we discuss the possibility that measurements are correct, and it is our understanding of cosmology that is wrong. In Sect. 5 we conclude, and in the spirit of our guide for consumers, we provide our buyer’s advice and recommendations. We aim to be impartial, and the views expressed here are solely our own. Busy readers could review Sects. 2, 4 and 5, and dip into Sect. 3 if more detail is needed.

For the remainder of this review, we adopt $c=1$ throughout the text.

Fig. 2

Summary of recent $H_0$ measurements. We have intentionally selected a limited number of results to show those that are as independent from each other as possible, in the sense that they use different photometric data, distance calibrators and so on. More comprehensive versions of this plot can be found for example in Di Valentino et al. (2021). Comments: (1) CCHP and Yuan et al. share a common distance to LMC as a calibrator. (2) TDCOSMO is a re-analysis of almost the same data as H0LiCOW, but with changes to the galactic potentials. (3) BOSS and DES share a prior constraint on baryon densities from BBN. (4) The results of Blakeslee et al. use new SBF observations, whereas Khetan et al. use archival SBF distances to calibrate SN Ia. The code use to generate this figure is publicly available at https://github.com/Pablo-Lemos/plot1d

1.1 Linking $H_0$ to H(z)

Hubble’s “constant” (Eq. 1) is not fixed when we observe beyond our local cosmological neighbourhood; which is to say it is not fixed in time. Therefore, we write $H_0 \equiv H(t_0)$, where $t_0$ is the present day and in general $H = H(t)$. The expansion has slowed down in the past, but the universe is now accelerating (since $z \sim 0.6$) and has been dark energy dominated since $z \sim 0.3$. The change in H(t) may be written using the phenomenological deceleration parameter q(t) as

$$\begin{aligned} \frac{\mathrm{d}H}{\mathrm{d}t} = -H^2 (t) (1+q(t)). \end{aligned}$$

(2)

In our local universe q(t) is approximately constant, and hence some authors adopt $q_0 \equiv q(t_0)$ as a constant (see for example Riess et al. 2016 or Freedman et al. 2019). As redshift is a monotonically decreasing function of time, we can write $H = H(z)$ and approximate

$$\begin{aligned} H(z) \simeq H_0 [1+ (1+q_0)z]. \end{aligned}$$

(3)

As $q_0 \simeq -0.55$, light travelling to us from more than $100 \;\,\hbox {Mpc}$ away will have been emitted when the Hubble constant was more than 1% different to its current value. The purpose of phrasing cosmography in this way is to avoid explicit assumptions on the matter or energy content of the universe, and it is of course possible to use more general parametrisations to expand H(z). While this approximation is reasonable for $z \ll 0.1$, if we wish to go further, or link phenomenological parameters to physical quantities, we need a cosmological model.

Cosmological models usually assume the universe is homogenous and isotropic on large scales, and has a space-time metric. Under those assumptions, the Friedmann–Robertson–Walker (FRW) metric is

$$\begin{aligned} \mathrm{d}s^2 = \mathrm{d}t^2 - a^2(t) \left(\frac{\mathrm{d}r^2}{1-k r^2} + r^2 (\mathrm{d}\theta ^2 + \sin {\theta }^{2} \mathrm{d}\phi ^2)\right), \end{aligned}$$

(4)

where a(t) is a scale factor defining how physical distances evolve with cosmological time t, and $(r, \theta , \phi )$ are comoving polar coordinates centered on ourselves. k is a curvature parameter, which here has units of inverse area as we wish to set $a(t_0) = 1$ (an alternative convention is to set $k = 0, \pm 1$ but it is not in general possible to do both). Results from Planck (Planck Collaboration 2020) for the CMB in isolation show a preference for mildly closed universe where $k>0$, and allowing k to vary from zero lowers the CMB derived $H_0$ to $63.6^{+2.1}_{-2.3} \; \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. However, most other observational evidence points to a flat universe (for example galaxy survey data or gravitational lensing of the CMB—see for example Efstathiou and Gratton 2020). Our discussion would not be materially affected by including spatial curvature, and for this review we will assume a flat universe where $k = 0$. We return to the point in Sect. 4.

The Hubble parameter is then defined as

$$\begin{aligned} H(t) = \frac{{\dot{a}}}{a}, \end{aligned}$$

(5)

where ${\dot{a}} \equiv da/dt$. The scale factor and redshift are related by

$$\begin{aligned} a(t) = \frac{1}{1+z_{\mathrm{cos}}(t)}. \end{aligned}$$

(6)

By $z_{\mathrm{cos}}$, we mean the redshift that would be seen if both the observer and emitter were stationary in comoving coordinates, which we take to be the frame in which the CMB has no dipole. Peculiar velocity is then the velocity with respect to this frame. We know the solar peculiar velocity relative to the CMB from our observed dipole, but to estimate $z_{\mathrm{cos}}$ from the observed redshift $z_{\mathrm{obs}}$ we also need the peculiar velocity of the emitter. For example, a 10% error in a peculiar velocity of $300 \;\hbox {kms}^{-1}$ of a galaxy lying at $50 \;\,\hbox {Mpc}$ away would result in a 1% error in $H_0$ were we to calculate it solely from that galaxy. For that reason, astronomers seek large numbers of objects distributed across the sky, deep into the “Hubble flow”, meaning their peculiar velocities are small compared to Hubble expansion and are assumed to average out. From here, we write $z = z_{\mathrm{cos}}$ unless indicated otherwise.

The ${\varLambda} {\text{CDM}}$ cosmological model is defined as

$$\begin{aligned} \left( \frac{H}{H_0} \right) ^{2} = \varOmega _{k,0} (1+z)^2 + \varOmega _{m,0} (1+z)^3 + \varOmega _{r,0} (1+z)^4 + \varOmega _{\varLambda ,0}. \end{aligned}$$

(7)

This can be generalised with an equation of state parameter $p = w \rho$ for dark energy where p is pressure, and the above corresponds to the cosmological constant $w = -1$. The fictitious curvature density is $\varOmega _{k} = 1 - \varOmega _m - \varOmega _r - \varOmega _{\varLambda }$, and we have assumed spatial flatness $\varOmega _{k} = 0$.

The present day density fractions for matter, radiation and dark energy $\varOmega _{i,0} \equiv \varOmega _i (z=0)$ are defined in terms of the physical densities $\rho _i$ as

$$\begin{aligned} \begin{aligned} \varOmega _i(z)&= \frac{\rho _i (z)}{\rho _{\mathrm{crit}}(z)}, \\ \rho _{\mathrm{crit}}(z)&= \frac{3 H^2(z)}{8 \pi G}.\\ \end{aligned} \end{aligned}$$

(8)

It is straightforward to expand H(a(z)) as a Taylor series in z and obtain Eq. (3) to first order where

$$\begin{aligned} q_0 = \left. -\frac{a \ddot{a}}{{\dot{a}}^2} \right| _{t=t_0}. \end{aligned}$$

(9)

So, in a narrow sense, a cosmological model is a function to derive H(z) from $H_0$ and $\varOmega _i$ or vice versa (provided nothing converts energy from one type to another). This is how $H_0$ is calculated from H(z) at $z \sim 1100$ for the CMB. Hence, one way to reconcile the Hubble tension is to change the function $H(z, \varOmega _i)$ by adding new energy components or novel interactions, and we return to this later.

1.2 Distances from angles and fluxes

Luminosity distance is defined to recover the standard inverse square law ratio between the bolometric luminosity L and flux F that would hold in a flat, static universe:

$$\begin{aligned} d_L^2 \equiv \frac{L}{4\pi F}. \end{aligned}$$

(10)

In a homogeneous and isotropic universe we find

$$\begin{aligned} d_L = \frac{(1+z_{\mathrm{obs}})}{H_0} \int _{0}^{z} \frac{\mathrm{d}z^{'}}{E(z^{'})}, \end{aligned}$$

(11)

where it is conventional to make the dependence on $H_0$ explicit by setting $H(z) \equiv H_0 E(z)$. Substituting in Eq. (7), for flat ${\varLambda} {\text{CDM}}$ we have

$$\begin{aligned} E(z) = \sqrt{\varOmega _{\varLambda ,0} + \varOmega _{m,0} (1+z)^3 + \varOmega _{r,0} (1+z)^4}. \end{aligned}$$

(12)

Angular diameter distance is the ratio between the physical size l of a distant object, and the small angle $\delta \theta$ it subtends on the sky:

$$\begin{aligned} d_A = \frac{l}{\delta \theta }. \end{aligned}$$

(13)

The Etherington relation (Etherington 1933)

$$\begin{aligned} d_L = (1+z_{\mathrm{obs}})^2 d_A \end{aligned}$$

(14)

is a useful way to convert between the two.²

To link ${\varLambda} {\text{CDM}}$ to our local universe, we expand Eq. (7) to second order in z:

$$\begin{aligned} \begin{aligned} H(z )&= H_0 [1+(1+q_0) z + (j_0 - q_0^2)\frac{z^2}{2}] , \\ d_L&= \frac{z}{H_0}[1+\frac{1}{2}(1-q_0)z - \frac{1}{6}(1 - q_0 - 3q_{0}^{2} + j_0)z^2], \end{aligned} \end{aligned}$$

(15)

where the jerk parameter $j_0$ is defined as

$$\begin{aligned} j_0 = \left. -\frac{a \dddot{a}}{{\dot{a}}^3} \right| _{t=t_0}. \end{aligned}$$

(16)

Eq. 15 is now a reasonable approximation to Eqs. (7) and (11) out to $z \sim 0.6$.

Setting $\varOmega _{r,0} \simeq 0$, we then obtain $q_0 = \frac{1}{2}(\varOmega _{m,0} - 2 \varOmega _{\varLambda ,0})$ and $j_0 = \varOmega _{m,0} +\varOmega _{\varLambda ,0} \simeq 1$.

Hubble’s law $v= H\, d$ is implicit in Eq. (11). Expanding the integral as a Taylor series in z, we see that $v = cz$ as used by Hubble and Lemaître (and re-introducing c here for clarity) is only valid as a low-z approximation.

1.3 The age of the universe

The age of the universe $t_0$ is inversely proportional to $H_0$, with dependence on other cosmological parameters. From the definition of $H(t) = {\dot{a}}/a$ we can write

$$\begin{aligned} t_0 = \int _0^1 \frac{\mathrm{d}a}{a H(a) }. \end{aligned}$$

(17)

In the special case of a flat, radiation-free universe, where we set $\varOmega _{m,0} + \varOmega _{\varLambda ,0} =1$, it can be written analytically as

$$\begin{aligned} t_0 = \frac{2}{3} \frac{1}{H_0} \frac{1}{\sqrt{1-\varOmega _{m,0}}} \ln \left[ \frac{1+\sqrt{1-\varOmega _{m,0}}}{\sqrt{\varOmega _{m,0}}}\right] . \end{aligned}$$

(18)

For a flat universe with $\varOmega _{m,0}= 0.3$ this gives $H_0 t_0 \approx 0.96$. Historically (in the 1980s), it was believed that the universe was Einstein–de Sitter ($\varOmega _{m,0}= 1.0$ and $\varOmega _{\varLambda ,0} = 0.0$), which yields the product $H_0 t_0 = \frac{2}{3}$. Then, a low value of $H_0 \approx 50 \; \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ was required to ensure that the universe is older than the oldest globular clusters. The existence of $\varLambda > 0$ makes the universe naturally older. The Planck estimate is $t_0 = 13.797 \pm 0.023\,\mathrm { Gyr}$ within ${\varLambda} {\text{CDM}}$ (Table 2 for Planck alone, 68% CL; Planck Collaboration 2020). This value for the age of the universe is comfortably larger than the age of any known astronomical object.

2 Inference of $H_0$

2.1 Standard candles and the nearby distance ladder

A standard candle is any population of stars or events which

• can be reliably identified

• have the same characteristics wherever they are seen

• have an established luminosity law specifying the absolute magnitude in terms of observable quantities.

Although the luminosity law is determined empirically by calibration (except in the case of gravitational waves—see Sect. 2.3), there is an advantage if there is also a solid understanding of the underlying physics of the standard candle as in that case the calibration can be cross-checked against a theoretically-derived one.

The nearby distance ladder starts with a choice of standard candle, and a calibration of the absolute magnitude M, for example using parallax distances and apparent magnitudes m. m is defined by

$$\begin{aligned} m_{X} = -2.5 \log _{10} \left( \frac{F_{X}}{F_{X, 0}} \right) , \end{aligned}$$

(19)

where $F_{X}$ is the energy flux per unit area per second across the wavelength range of the band X, and $F_{X,0}$ is the fixed reference flux for the magnitude system being used (for example the Vega system). M is the apparent magnitude the object would have if it were at a distance of 10 parsecs. Distance is conveniently quoted as the distance modulus

$$\begin{aligned} \,\mu = m-M, \end{aligned}$$

(20)

and then the luminosity distance (10) becomes

$$\begin{aligned} d_L = 10^{0.2(\,\mu +5)} \; \text{ parsecs }, \end{aligned}$$

(21)

which can then be substituted into Eqs. (11), (15) or similar relations to obtain $H_0$.

A given standard candle seen over a range of distances is termed a “rung”, and in turn used as calibrators for the next rung. For example, the SH0ES team (Riess et al. 2019) calibrate Classical Cepheids (CC) using parallaxes, a maser distance to NGC4258, and detached eclipsing binaries (DEBs) in the LMC as their first rung. Their next rung is Type Ia supernovae (SN Ia), calibrated using the 19 galaxies in which both Cepheids and SN Ia have been observed. We illustrate their construction in Fig. 3.

Fig. 3

Our schematic illustration of the construction of distance ladders. Green circles represent the calibration of the distance ladder (either the base or overlap of each rung), and the bars are the rungs of the distance ladder. The size of dots or thickness of bars are in proportion to their contribution to the error budget of $H_0$; in the case of the CMB and BBN we have opted for a thin line to show the dependence on ${\varLambda} {\text{CDM}}$

The quality of the standard candle depends on a number of considerations. Are there enough with good distances to accurately calibrate the absolute magnitude? Can we clearly identify them at large distances? Can they be observed out to a sufficient distance to reach the next rung? Are the objects observed at large distances of the same type as local ones used as calibrators? How to correct for extinction, reddening, metallicity effects and crowded starfields? Which band has the most reliable magnitudes? If data have been combined from different telescopes, have the right adjustments been made to convert photometry? How is magnitude to be defined for variable stars? Each rung depends on the previous one, and errors will propagate up the ladder.

A more subtle issue is that the conversion of observational data to $H_0$ is non-linear. As the expectation ${\mathbb {E}}[d^n] \ne {\mathbb {E}}[d]^n$ in general, scatter in observational data will introduce systemic bias. Bias can also be introduced by sample selection unless care is taken as ${\mathbb {E}}[d_1< d < d_2] \ne {\mathbb {E}}[d]$: we average our selected sample but wish to know the expectation of the unselected one. Selection may be overt (for example by cutting outliers) or due to our telescope seeing only up to $m < m_0$ (known as Malmquist bias; Malmquist 1922). Both of these can be (and usually are) corrected for, but require some assumptions and a careful analysis of the data and reduction pipeline.

2.2 Standard rulers and the inverse distance ladder

A standard ruler is a feature on the sky of a known physical size l, which enables us to calculate the angular diameter distance $d_A$ defined in Eq. (13) from their angular size. Parallax is an obvious example, and also the size of orbits of masers and detached eclipsing binaries can be determined from their positions, light curves and spectroscopy. In the early universe, acoustic pressure waves in the primordial charged particle and radiation plasma set a physical size called the sound horizon $r_s$, which is how far they travel from the initial seeds³ that generate them. The universe was not that dense at that time, so Thomson scattering by charged particles was necessary to propagate the waves, and hence they are frozen-in by recombination. The sound horizon is then imprinted on the CMB as peaks in the power spectrum of temperature fluctuations, and in the later spatial distribution of galaxies (known as baryon acoustic oscillations, or BAO for short).⁴ The sound horizon may be calculated in a cosmological model, and depends both on the expansion rate H(z) (the waves are carried along by expanding spacetime) and the matter-energy content of the early universe (determining the sound speed).

The inverse distance ladder, as its name suggests, works in the opposite direction to the nearby distance ladder but on the same principle. It can use the sound horizon for a starting $d_A$, a background cosmology, and the Etherington relation (14) to calibrate the luminosity distances $d_L$ of standard candles. For example, Lemos et al. (2019) calibrate BAO at $z \simeq 1$ and SN Ia at $z<1$ using the CMB sound horizon. They replace the standard ${\varLambda} {\text{CDM}}$ formula for H(z) with a parametric form. H(z) is extrapolated to today to find $H_0 = 68.42 \pm 0.88 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. Thus, it is shown that discrepancy between the CMB value of Planck Collaboration (2020) and Riess et al. (2019) is not caused by assuming the late-universe is ${\varLambda} {\text{CDM}}$.

We can express the difference between early and late universe $H_0$ in terms of ruler size or luminosity differences. Planck implies $r_s = 147.27 \pm 0.31$ Mpc in ${\varLambda} {\text{CDM}}$; it would need to be $\simeq 10$ Mpc lower (Knox and Millea 2020) to bring consistency with Riess et al. (2019). Alternatively, Eqs. (21) and (11) show that Cepheids or SN Ia would need to be $\simeq 0.2$ mag brighter than thought to bring consistency with Planck.

In summary, we see the two ways of constructing ladders, propagated toward each other by the “guard rails” of SN Ia, do not meet! Hence, the $H_0$ tension is sometimes characterised as “early” versus “late”, from which follows the question “Is ${\varLambda} {\text{CDM}}$ right?”. This may be premature: in fact, few late-universe results in isolation are fully inconsistent with early universe ones, as we discuss later.

2.3 No-ladder $H_0$

We have seen distance ladders require calibration, whether they are nearby or inverse. However, there are some self-calibrating observations from which $H_0$ may be calculated directly.

One example is the CMB. The detailed shape of the power spectrum determines other parameters in ${\varLambda} {\text{CDM}}$, and the value of $H_0$ derived from it is best understood as just one part of the simultaneous inference of all cosmological parameters. A further example is maser emission systems, which occur in the nucleus of certain galaxies and are bright enough to be seen at cosmological distances. The emission spots appear to follow Keplerian orbits, and so with some disk modelling, the size of the orbit and hence the angular diameter distance can be deduced directly.

Gravitational waves assume general relativity. The masses of merging compact objects and luminosity can be obtained from the shape of the waveform. That is to say, there is no need for an empirical calibration of their intrinsic luminosities, and instead the observational challenge is to determine the redshift of the source. Often referred to as standard sirens rather than standard candles, a gravitational wave event whose source galaxy has been identified (by locating the optical counterpart) is referred to as a “bright siren”, otherwise it is called a “dark siren”. Most gravitational wave events are dark, but progress can be made statistically with them given sufficient numbers.

For gravitational lenses, general relativity links the time delay caused by the lensing of the background source (a combination of both the longer path and time dilation) and the mass distribution of the lensing galaxies. The absolute time delay is not known, but if a rapidly varying source like a quasar can be seen in multiple images, the relative time delay between images allows the angular diameter distance of the lens to be calculated. In this case, the challenge is to obtain enough constraints on the mass distribution of both the lensing galaxies and the general concentration of matter along the line of sight, using for example the velocity dispersions and surface brightness of the lensing galaxies, and imaging data.

2.4 What could cause the tension?

Using the word “tension”, cosmologists mean the discrepancy in measurements of $H_0$ is at a level which is large compared to the reported errors. This means that if the values and errors are correct, this is very unlikely to be the result of chance.

Measuring the Hubble constant has always pushed the limits of the available telescopes of the day, and as a consequence observers have to be very careful to avoid bias in their derivations of $H_0$, and have accounted for all errors. Hubble believed he had one population of Cepheids, whereas we know today he had two, and had also confused nebulae with bright stars. Alternatively, many researchers interpret the tension in the spirit of the precession of the perihelion of Mercury: something is wrong with the (Newtonian) model and a new one is needed (general relativity). We can categorise explanations as follows:

• Observational bias. An observational bias is an error in mean photometry that would be expected to increase with magnitude or distance. To give some examples, consider first crowding. For distant stars, resolving them from their neighbours becomes harder, therefore, their photometry will be progressively more blended with other stars the more distant they are. Blending increases the apparent magnitude, and changes the colour (see for example the discussion in Sect. 4.2 in Javanmardi et al. 2021). For very faint stars, the response of the detector may be non-linear (Riess et al. 2019), and needs to be corrected. Another issue is combining observations between ground and space telescopes, as in general fainter stars will be observed from space, but nearby ones more cheaply from the ground. Aside from atmospheric extinction, each instrument has different passbands, detector response and resolution, meaning the magnitudes of the same star observed in each telescope will be different. Photometry must be transformed to a common system (see for example Eqs. 10–12 in Riess et al. 2016), and if not done (or done incorrectly) some bias will likely have been introduced. Any parameters derived from photometry—such as photometric redshifts—would inherit the same propensity to bias.

• Astrophysical bias. An astrophysical bias occurs when the properties of the object being studied are not fully resolved, and those properties differ with distance. For example, consider Cepheids in the LMC and SN Ia hosts. The LMC is close so Cepheids with a full range of periods can be seen, whereas for distant galaxies only the brighter Cepheids with longer periods are seen. Additionally, the LMC is metal-poor compared to a typical spiral galaxy, the Cepheids there may be expected to be relatively metal-poor compared to those in SN Ia hosts. Hence, any curvature in the Leavitt law, or mis-calibrated metallicity dependency could bias distances (see for example Freedman and Madore 2010). A second example is the step-like link between SN Ia magnitudes and properties of the host galaxy (Smith et al. 2020 and references therein). This could indicate there are two distinct populations of SN Ia. If then the SN Ia in the 19 galaxies where both Cepheids and SN Ia were of mostly one type, whereas the rest a blend of both types, $H_0$ would be biased by the calibration of SN Ia.

• Statistical bias. The main causes of statistical bias will be selection effects and scatter as we discussed in the introduction. Statistical biases can be corrected by running random simulated observations through the same selection and analysis pipeline, but the simulations will themselves need some physical parameter choices, perhaps determined from previous surveys, or fixed in advance to “reasonable” levels. In Bayesian analysis, residual dependence on the choice of prior is a feature of sparse observations. Statistical bias correction is subtle and difficult, as we see later in the sections on parallax and SN Ia.

• Physics of ${\varLambda} {\text{CDM}}$. Before invoking new physics, could the explanation be found within ${\varLambda} {\text{CDM}}$? Cosmological formulae such as Eq. (7) are derived from a homogeneous, isotropic universe. Could corrections allowing for inhomogeneities be large enough to explain the tension? A specific example is the “Hubble Bubble” or local void proposal (for a recent example, see Shanks et al. 2019), in which we are by chance located in an under-dense region, and our local $H_0$ is different from the “universal” one. Additionally, inhomogeneities mean we must correct redshifts for peculiar velocities, and further the propagation of light through overdense or underdense regions might bias our analysis (Kaiser and Peacock 2016).

• New Physics. If the expansion history of the universe were different to ${\varLambda} {\text{CDM}}$, $H_0$ inferred from the CMB or BAO might be brought into alignment with the local value. Alternatively, performing our analysis of a non-${\varLambda} {\text{CDM}}$ universe using ${\varLambda} {\text{CDM}}$ formulae may have confused us. For example, an extra particle species would increase the pre-recombination expansion speed, so reduce the size of the sound horizon: sound waves have less time to propagate before they are frozen in. To keep the same observed angular size of the CMB temperature fluctuations, the value of $H_0$ calculated from the CMB will increase (see Eqs. 11, 13, 14). However, as we see later ${\varLambda} {\text{CDM}}$ makes many other successful predictions, such as the CMB spectrum itself or primordial element abundances, and is not lightly tampered with.

2.5 Is the tension significant?

The tension is often quoted as the number of standard deviations “$m\sigma$”. In particle physics, the meaning is clear: there are millions of collisions and probability is frequentist. There is no need to work in a Bayesian framework, with some prior assumption of a parameter to update with new data. The law of large numbers drives distributions to Gaussian normal shape, and we can translate $m\sigma$ to a probability of occurrence by chance. At the $5\sigma$ level, it is unanimously agreed new physics has been detected. None of the above applies in cosmology!

Nevertheless, that the tension is significant should not be in doubt: see Fig. 2. But we are looking for more from our data analysis, and there are three ways in which Bayesian statistics are helpful, which we now briefly survey.

Bayes’ theorem states that the posterior probability distribution is

$$\begin{aligned} P (\theta \mid D, {\mathcal {M}}) = \frac{P (D \mid \theta , {\mathcal {M}}) P(\theta \mid {\mathcal {M}})}{P(D \mid {\mathcal {M}})}, \end{aligned}$$

(22)

where D is the data and $\theta$ are the parameters of the model ${\mathcal {M}}$ of interest. For example ${\mathcal {M}}$ might represent ${\varLambda} {\text{CDM}}$ with its associated parameters including $H_0$ and ${\mathcal {M}}_{1}$ some extension of it with additional parameters. $P(\theta \mid {\mathcal {M}})$ is any prior belief in the parameters of the model and $P (D \mid \theta , {\mathcal {M}})$ is called the likelihood, typically specified by the team analysing the data. The denominator

$$\begin{aligned} P(D \mid {\mathcal {M}}) = \int _{\varTheta } P (D \mid \theta , {\mathcal {M}}) P(\theta \mid {\mathcal {M}}) \mathrm{d}\theta , \end{aligned}$$

(23)

is called the evidence. An extended cosmological model will have a smaller evidence if there exist large values of the parameter space with low likelihood, even if it agrees better with the data. Bayesian evidence then naturally embodies Ockham’s razor: a simpler model will have a larger evidence, unless the extended model has a significantly better fit to the data.

Second, Bayesian statistics can also help in re-analysis, in the hope that the data itself may reveal issues. A Bayesian hierarchical analysis was used by Feeney et al. (2018) to test relaxing distributional and outlier assumptions embedded in the $\chi ^2$ fit used in SH0ES analyses. Cardona et al. (2017) have re-analysed SH0ES data using “hyperparameters”, which are weightings of datasets proposed as a measure of credibility by Lahav et al. (2000). An agnostic prior for the weights is set, and the hyperparameters are marginalised over. Both results are consistent with SH0ES. Bernal and Peacock (2018) extend the hyperparameter method by adding a free parameter shift in the mean of each dataset to account for unknown systematics, which they dub “BACCUS”. Using this to combine Planck, SH0ES and other datasets, produces a compromise. As shown in Fig. 4, the posterior middles the two with much larger error bars, which perhaps is unsurprising given the agnosticism of the method. Such types of analysis need to be taken with a grain of salt: data that is in tension should not be combined, and BACCUS is not a substitute for a critical analysis of why the tension has happened. However, if one demands a method to merge disparate results in a Bayesian framework, BACCUS is a way to achieve that.

Fig. 4

An illustration of BACCUS applied to Planck, H0LiCOW and SH0ES data, whose posteriors are shown as thin grey lines. Conventional (orange) is the standard Bayesian combination assuming equal weighting, w/Rescaling (blue) is equivalent to hyper-parameters, w/Shifts (brown) adds an unknown systemic error offset to each dataset, and w/Shifts + Rescaling (green) combines hyper-parameters and systemic offsets. Image reproduced with permission from Bernal and Peacock (2018), copyright by IOP/SISSA

Third, we may want to know how valid a combination of data sets is. If two posteriors for the same parameter barely overlap, a Bayesian analysis will seriously mislead with error bars that are too small, as shown by the yellow line in Fig. 4. We seek a statistic that is symmetric, (reasonably) independent of prior assumptions and models, and straightforward to calculate and interpret. The R statistic

$$\begin{aligned} R = \frac{P(D_A, D_B)}{P(D_A) P(D_B)} = \frac{P(D_A \mid D_B)}{P(D_A)} = \frac{P(D_B \mid D_A)}{P(D_B)} \end{aligned}$$

(24)

compares the evidence of dataset $D_A$ in light of knowing $D_B$ to that of $D_A$ alone, but is dependent on the prior and so is not usually comparable between different papers. Handley and Lemos (2019) define a new statistic called “suspiciousness” as

$$\begin{aligned} \log S = \log R - \log I, \end{aligned}$$

(25)

where I is the information ratio $\log I = {\mathcal {D}}_{A} +{\mathcal {D}}_{B} - {\mathcal {D}}_{AB}$ which quantifies the information gain between prior and posterior. ${\mathcal {D}}_A$ is defined as

$$\begin{aligned} {\mathcal {D}}_A = \int _{\varTheta } P(\theta \mid D_A) \log \frac{P(\theta \mid D_A)}{P(\theta )} \mathrm{d}\theta , \end{aligned}$$

(26)

and ${\mathcal {D}}_B$ and ${\mathcal {D}}_{AB}$ are defined similarly by replacing $A \rightarrow B, AB$, respectively. This is independent of the prior and (being an integral) the choice of parameters. We can interpret $\log S \ll 0$ as the two data sets being in tension: loosely speaking, the evidence of combining them does not exceed the information of considering them separately. Therefore, suspiciousness fits the criteria of simplicity and interpretation we outlined above.

Finally, even in light of the tension, we cannot dodge the question posed in our introduction: “All this debate is interesting, but which value for $H_0$ should I use, and is it valid to use that in ${\varLambda} {\text{CDM}}$?”. We suspend judgement until after we have surveyed the data and potential new models.

3 Measuring $H_0$

3.1 Parallax

Parallax is both the oldest astrometric technique, and the easiest to understand. Hold out your thumb at arm’s length, relative to some fixed point on the wall, and alternately close one eye and then the other. Relative to the fixed wall, the apparent position of your thumb will change, and this is how our depth perception works: the smaller the change in position, the longer your arm must be. The same principle works with stellar distance, where now our “binoculars” correspond to the Earth’s position on opposite sides of its orbit. The change in a fixed star’s position $2\varpi = \theta _1 - \theta _2$ arcseconds, due to the change in the Earth’s position by 2 a.u. over 6 months leads to the distance $d = 1/\varpi$ parsecs.⁵ Our measurement of position must be very precise. Although the nearest star, Proxima Centauri, has a parallex of approximately 0.77 arcseconds, modern measurements target a remarkable 10 $\,\mu$as, which is the size of a thumbnail on the Moon as seen from Earth.

Modern parallax measurements began with the satellite Hipparcos (the name alludes to the ancient Greek astronomer Hipparchus, who measured the distance to the Moon). Launched by the European Space Agency in 1989, it measured the parallaxes of 100,000 stars at an accuracy of up 0.5 milliarcsecond (mas), the fixed background frame now being extragalactic sources such as quasars. Although undoubtedly impressive, at 1000 light years an error of 0.5 mas would still be a distance error of 15%. A further drawback is Cepheids, an important part of the distance ladder we discuss shortly, are relatively rare stars and only a handful are located in our neighbourhood of the Milky Way.

Moving on to the present day, our two best current sources of parallax are Gaia and the Fine Guidance Sensor/Wide Field Cameras (FGS/WFC3) aboard the Hubble Space Telescope (HST). Gaia was launched in 2013 and the mission goal is to measure over a billion stars (including 9,000 Cepheids and half a million reference quasars), both in our galaxy and satellites like the LMC. The mission-expectation precision is 7$\,\mu$as at $m=12$, rising to 26$\,\mu$as at $m=20$ (Gilmore 2018). Gaia does this by slowly scanning the sky with two telescopes set at relative angles of ${106.5}^{\circ }$, to make a one-dimensional measurement of the time and position of each star that slowly drifts across the CCD. Up to 70 measurements will be made for each star, which allows the additional calculation of proper motions, and even small changes in position caused by the gravitational tug of planets orbiting the star. The HST operates on similar principles in “spatial scanning” mode; although it cannot survey like Gaia, when focused on nearby Cepheids its errors appear competitive (Riess et al. 2018a).

Gaia’s high precision is dependent on a very stable mechanical structure of the spacecraft. A variation in the angle between the two fields (which might be caused by thermal expansion) could cause spatial variations in apparent parallax, or if synchronous with the scan period even a fixed systematic offset. Indeed, such a variation has been inferred from the interim Data Release 2 (DR2) (Gaia Collaboration 2018). The average of the quasar parallaxes in it is $-29\,\mu$ as (negative parallaxes can happen when position measurement error is larger than the parallax), and there were indications this “zero point” may vary with stellar colour, luminosity and position on the sky (Arenou et al. 2018). Riess et al. (2018b) compared HST Cepheid parallaxes to Gaia, simultaneously solving for the Gaia zero point and Cepheid calibration. They found a difference between them $46\pm 15 \,\mu$ as, with Gaia parallaxes again appearing too low. As the typical parallax of a Milky Way Cepheid is $400\,\mu$ as, this is very material to distance estimates. Breuval et al. (2020) creatively replaced DR2 Cepheid parallaxes with those of resolved bound binary companions (where available), which being dimmer are closer to the ideal magnitude range for Gaia.

During the preparation of this review, Gaia Early Data Release 3 was made available, and has already by used by Riess et al. (2021) to revisit Gaia parallaxes. Gaia EDR3 is not intended to be the final word, but indeed Cepheid zero points seem now to be reduced below $10\,\mu$ as. A calibration of Cepheids using 75 Gaia parallaxes only gives $H_0 = 73.0 \pm 1.4 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$, which is slightly lower, but consistent with their previous result based on HST parallaxes.

Before moving on to discuss alternative calibrations, we will first digress into a discussion of parallax bias. The potential for bias occurs in any astrophysical observation, and is often the subject of lengthy analysis in $H_0$ papers. As it is most easily understood in the context of parallax, it is helpful to discuss it here.

Parallax bias is usually referred to as Lutz–Kelker–Hanson (LKH) bias (Lutz and Kelker 1973; Hanson 1979). This is a summation of three quite different effects: non-linearity of the desired variable (distance) with respect to the observed variable (parallax), population bias (have we observed the object we intended to, or did we confuse it with something else?), and selection bias (our surveys are normally magnitude limited, so we will only “select” objects for which $m<m_0$).

To explain non-linear bias, imagine we have a symmetric error in our parallax measurement, such as might be caused by an instrumental point spread function. To be concrete, suppose the likelihood of measuring $150\,\mu$ as is the same as measuring $50\,\mu$ as when $100\,\mu$ as is the true value. If we average the distance, we will obtain ${\bar{d}} = 6666.67 + 20000 = 13,333$ which is biased with respect to the true distance of 10,000 parsecs. In mathematical terms, because $d = 1/\varpi$, then ${\mathbb {E}}[d] \ne 1/{\mathbb {E}}[\varpi ]$.

Population bias arises in parallax when we consider a broad survey of stars at a given distance r from our position. Assuming a roughly constant spatial density of similar stars, there are more stars in the shell $(r, r+\varDelta r)$ than there are in the shell $(r - \varDelta r, r)$ for some finite $\varDelta r$. Hence, there are more (further) stars whose parallaxes may be over-estimated to place them at r than (closer) stars whose parallaxes may be over-estimated. Taken to extremes, there are huge numbers of stars with effective parallaxes of zero, waiting for their small but finite chance to “crowd in” to a given measured parallax. This will bias observed parallaxes too low. Note that if we were certain of our identification of the star (as we would be for a Milky Way Cepheid close to us), we need not consider population bias: it would stand out from the crowd (Fig. 5).

Fig. 5

An illustration of Lutz–Kelker–Hanson population bias. Assume each parallax measurement can be in error by up to $\pm \delta \varpi$. In the figure on the left, there is a constant spatial density of stars. Then, the region $(\varpi , \varpi -\delta \varpi )$ has a greater number of stars that can scatter to the observed parallax $\varpi$ than the region $(\varpi , \varpi +\delta \varpi )$ and parallaxes are biased too low. Conversely in the figure on the right, the stellar density drops sharply beyond $\varpi$ due to either the edge of the population or magnitude limitations. More stars are available to scatter out than in, and parallaxes are biased too high

Conversely, suppose we were observing close to our magnitude limitations. Now the opposite bias would occur: we cannot see the further stars, so they cannot crowd in. But the same number of closer stars are available to crowd out, so our observed parallaxes will now be biased too high. This is the well-known Malmquist bias (Malmquist 1922), and is a major issue for surveys as naturally we will try to see as far as we can!

To deal with bias then involves modelling of the instrumental error, the selection function, the population scatter and so forth. In modern surveys, this is normally done by constructing simulated catalogs with known physical parameters and some assumptions, and putting those catalogs through the same analysis pipeline as the real data to see what biases emerge. For example, Riess et al. (2018a) compute distance modulus biases of between 0.03 and 0.12 mag for MW Cepheids using a model for galactic stellar distributions. If working in a Bayesian framework, a posterior distribution for the distance may be derived using the method of Schönrich et al. (2019). An alternative is to work directly with the parallaxes, instead converting Cepheid magnitudes to predicted parallaxes as done by Riess et al. (2018b). As the magnitudes are measured considerably more accurately than the parallaxes, bias corrections to the magnitude to parallax conversion are not necessary. To check the predictions of LKH bias, Oudmaijer et al. (1998) compared ground-based to Hipparcos parallaxes, finding a bias towards brighter magnitudes up to relative error $\approx 30\%$, and dimmer magnitudes for larger error when Malmquist bias is dominant, as one would expect from the discussion above.

We end our digression on biases here and move on to discuss other geometrical distances.

3.2 Detached eclipsing binaries

Imagine we had a star for which we knew the surface radiant flux density J, and the physical size R. The stellar luminosity would straightforwardly follow as $L = 4\pi R^2 J$, and we would have a standard candle.

Cool, stable, helium-burning giants (that is, red clump) are sufficiently bright to be seen outside the Milky Way. For these “late-type” stars, just such an empirical relationship can be established for the surface brightness $S_V$ defined as

$$\begin{aligned} S_V \equiv V + 5 \log (\phi ) \;\;\text{ mag } , \end{aligned}$$

(27)

where $\phi$ is the stellar angular diameter, and V the visual band magnitude. This relationship has been calibrated by angular diameters obtained from optical interferometry of nearby stars, and is given by

$$\begin{aligned} S_V = (1.330 \pm 0.017) \times ((V-K) - 2.405) +(5.869 \pm 0.003) \;\;\text{ mag } , \end{aligned}$$

(28)

where $V-K$ is the colour difference between magnitudes in the V and $2.2 \;\,\mu$m near-infrared K band (Pietrzyński et al. 2019). The scatter is just 0.018 mag. Rearranging the definition of surface brightness and with $\phi = 2R / d$ it then follows that

$$\begin{aligned} d = 9.2984 \times \left( \frac{R}{R_{\odot }}\right) (10^{0.2(V - S_V)} \;\text{ mas}) \;\; \text{ parsecs }, \end{aligned}$$

(29)

where R and $\phi$ have been converted to solar radii and milli–arcseconds, respectively. The pre-factor is purely geometric.

But how can we know the radius of distant stars? Eclipsing binaries allow just that. If the stars are well separated enough to spectroscopically resolve each one,⁶ but close enough to eclipse each other, we can obtain their individual surface brightnesses, colours, radial velocities, eclipse depths and shapes, and the orbital period. With this data, the radius (and other physical parameters such as mass, eccentricity and inclination of the orbital plane) of each star can be solved for. Such an alignment of the stars is of course rare, but sufficient numbers do exist! By painstakingly observing 20 systems in the LMC over more than 20 years (covering many eclipses) Pietrzyński et al. (2019) determine the stellar radii to 0.8% accuracy. Crowding can be easily spotted in the light curve and removed. They derive $\,\mu _{\mathrm{{LMC Centre}}} = 18.477\pm 0.004\; \text{(stat) } \pm 0.026\; \text{(sys) }$, where the main contribution to the systemic error budget is the $S_V$ relation above.

This is the most accurate measurement of the distance to the LMC to date. As we shall see shortly when we discuss standard candles, this result has become key to many recent $H_0$ results: every standard candle can be found in the LMC, and the low error budget allows for a very accurate calibration.

Looking forwards, although DEBs have been found in M31 they are “early-type” stars with hot atmospheres, for which a reliable surface brightness to colour relation has not been established. The hope is future 30 m-class telescopes will have sufficient spectroscopic resolution to extend this to late-types in M31 and other local group galaxies (Beaton et al. 2019).

3.3 Masers

Maser emission occurs when thermal collisions in warm gas in an accretion disk around the central black hole of a galaxy drive a population inversion of molecular energy levels. Such systems are rare: the disk must be “just right”, not too hot, and not too cold, and have suitable local molecular abundance. The Type 2 Seyfert galaxy NGC 4258 at a distance of 7.5 Mpc is just such a system. Isolated bright spots of 22.235 GHz maser emission (from a hyperfine transition of ${\mathrm {H}}_{2}{\mathrm {O}}$) can be seen in three regions on the sky stretching 20 mas ($\sim 0.1$ ly) long, with the overall shape of a warped line. After subtracting the overall system redshift, the spots on one side are blue-shifted by $\sim 1000 \,\hbox {kms}^{-1}$, the other side is red-shifted by the same amount, and the spots in the middle are low velocity (Argon et al. 2008). If the spots are observed for long enough, their accelerations and proper motion can be obtained from the steady drift of their Doppler velocities and positions. The central spots show the lowest l.o.s. velocity and highest acceleration, and the outer spots having the highest velocity and lowest l.o.s. acceleration.

The key assumption these observations support is that all the spots form an orbital system with shared parameters, as it is anticipated that disk viscosity will have reduced the orbits to close to circular. The disk shape is then modelled (including such parameters as inclination, warp, residual eccentricity and so forth), fitted and the orbital parameters of the spots derived. The outer dot velocities v show a Keplerian behaviour with radius: $v^2 \propto GM/r$, and as the acceleration is then ${\dot{v}} \propto GM/r^2$, the physical radius of the system can be determined. The angular diameter distance is then

$$\begin{aligned} d_A = \frac{v^2}{{\dot{v}} \times \theta } , \end{aligned}$$

(30)

where $\theta$ is the angular impact parameter. Humphreys et al. (2013) have observed NGC 4258 for 10 years at 6 monthly intervals using VLBI interferometry, which resolves the relative position of the maser spots to $<3\;\,\mu$as accuracy (even the tectonic drift of the ground radio telescopes must be corrected for). The Doppler shifts are measured to within an accuracy of $1 \;\hbox {kms}^{-1}$, and the central spots accelerate by $\sim 10\;\hbox {kms}^{-1} \mathrm {yr}^{-1}$. The proper motions ${\dot{\theta }} \;\,\mu \text{ as } \text{ yr}^{-1}$ provide additional information as $d_A = v / {\dot{\theta }} \; \text{ Mpc }$. This pattern fits an accretion disk orbiting a $10^7 \,M_{\odot }$ black hole.

Fig. 6

The UGC 3789 maser system, showing the warped disk, velocities and acceleration of maser spots. The top left and top right figures show the LOS velocities in $\hbox {kms}^{-1}$ relative to the central blackhole, offset by position in milliarcseconds; the GM/r curve shape is apparent. The top centre panel shows the LOS acceleration in $\hbox {kms}^{-1}$ per year, calculated from the velocity drifts over 3 years of observations. In the bottom panel, we schematically show the warped disk and projected spots. UGC 3789 is at a distance of 46 Mpc so 1 mas $\simeq 0.24$ pc. The disk and maser spot data is available in Reid et al. (2013)

Reid et al. (2019) derive the distance as $d=7.576 \pm 0.082 \text{(stat) } \pm 0.076 \text{(sys) }$ Mpc, an accuracy of 1.4%, competitive with the LMC distance error. The main statistical contribution to the error budget is the positional error of the $\sim 300$ spots.

Only 8 megamaser galaxies have been detected, with the furthest being NGC 6264 at 141 Mpc, and it is unlikely more will now be found at usable distances. We illustrate the data for UGC 3789 from Reid et al. (2013) in Fig. 6a, b. The Megamaser Cosmology project (Pesce et al. 2020) have used six of these galaxies to find $H_0 = 73.9 \pm 3.0 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$, independently of distance ladders.

Although it is too close to determine $H_0$ directly (as its peculiar motion could be a large fraction of its redshift), NGC 4258 has become a key calibrator of the distance ladder, owing to its low error budget. Its particular usefulness is that, unlike the LMC or SMC, it is a fairly typical barred spiral galaxy, similar in morphology and environmental conditions (metallicity, star-formation rate and so forth) to the ones in which Cepheids and Type Ia supernovae are seen at greater distances. Using Cepheid and SN Ia data from Riess et al. (2016), Reid et al. (2019) find $H_0 = 72.0 \pm 1.9 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ using solely NGC 4258 as the geometric calibrator.

3.4 Cepheids

Having discussed calibrators, we can now talk about the “engine room” of distance ladders. Cepheids form two classes, but it is the younger, population I, classical Cepheids which are of interest. These are yellow bright giants and supergiants with masses 4–20 $M_{\odot }$ and their brightness cycles over a regular period, between days and months, by around 1 magnitude. They are bright, up to 100,000 $L_{\odot }$, and they can be seen out to 30 Mpc with the HST. Although Milky Way Cepheids had been observed and catalogued since the 18th century, it was first discovered by Henrietta Swan Levitt in 1908 that there was linear relation between the logarithm of their oscillation period and absolute magnitudes, the Leavitt period-luminosity law (we use the term P-L law for Miras). She had been observing Cepheids in the SMC and LMC, using the Harvard College Observatory telescope, and decided to rank them in order of magnitude. As stars in the LMC will have roughly the same distance from the Earth, the Leavitt law was immediately clear from their apparent magnitudes. In fact, one could say modern extragalactic astrometry began with her groundbreaking discovery.

That stars can pulsate is not so surprising; after all, a star is in local equilibrium, and would be expected to oscillate about the equilibrium given any perturbation. However, something must drive the oscillation otherwise it would dissipate. For Cepheids, the driver is heat-trapping by an opaque layer of doubly-ionised He surrounding a He-burning core. The trapped heat increases pressure, which expands the star, cooling the ionised He to the point where it can recombine and, therefore, becomes transparent. As the radiation escapes, the core cools and re-contracts, which in turn releases gravitational energy into the He layer. The He heats, re-ionises and the cycle repeats, with period proportional to the energy released. The Cepheid population lies in an instability strip in the horizontal branch of the Hertzsprung–Russell diagram; the cool (red) edge of the population is thought to be due to the onset of convection in the He layer, and the hot (blue) edge by the He ionisation layer being too far into the atmosphere for pulsations to occur. They, therefore, form a well-defined population.

A straightforward understanding of the origin of the Leavitt law can be found in thermodynamic and dynamic arguments. The luminosity of a Cepheid will depend on its surface area via the Stefan–Boltzmann law $L = 4\pi R^2 \sigma T^4$, which expressed in bolometric magnitudes is

$$\begin{aligned} M = -5 \log _{10} R - 10 \log _{10} T + \text{ const. } \;\;. \end{aligned}$$

(31)

The stellar radius can be mapped to the period by writing an equation of motion for the He layer as

$$\begin{aligned} m \ddot{r} = 4 \pi r^2 p - \frac{G M m}{r^2}, \end{aligned}$$

(32)

where r denotes the radial position of the layer, p is the pressure and m the mass of the layer. For adiabatic expansion, it is then straightforward to solve for the period P and we find $P \sqrt{{\bar{\rho }}} = \text{ const. }$ where ${\bar{\rho }}$ is the mean density (for further details see Cox 1960). With ${\bar{\rho }} \propto \; R^{-3}$ and temperature mapped to colour $B-V$, we obtain the Leavitt law as

$$\begin{aligned} M = \alpha \log _{10} P + \beta (B-V) + \gamma , \end{aligned}$$

(33)

where P is the period in days, $\alpha$, $\beta$ are empirically calibrated from the Cepheid data, and for the zero-point $\gamma$ we need a distance measurement.

It is preferable to use so-called Wesenheit magnitudes, which are constructed to be reddening-free, and have a reduced colour dependence (intrinsically redder Cepheids are fainter). Let’s see how this works in practice. Riess et al. (2019) define an NIR Wesenheit magnitude $m_H^W \equiv m_{\mathrm{F160W}} - 0.386(m_{\mathrm{F555W}} - m_{\mathrm{F814W}})$ using HST filter magnitudes, where the numerical constant is derived from a reddening law. They observed 70 LMC Cepheids with long periods, and after setting $\beta = 0$, they derive $\alpha = -3.26$ with intrinsic scatter 0.075 mag. By comparison, the scatter using solely optical F555W magnitudes is 0.312 mag. After subtracting the DEB distance modulus (Pietrzyński et al. 2019), we obtain $\gamma = -2.579$. The formal error in the Cepheid sample mean is 0.0092 mag, equivalent to 0.42% in distance (Fig. 7).

Fig. 7

Illustration the Leavitt law in four galaxies used for the local distance ladder. The LMC and N4258 are the two main calibrators of Cepheid distances. For the two example SN Ia hosts N4536 and N1015, it is harder to observe the fainter, shorter-period Cepheids. The slope is fixed at $-3.26$, corresponding to the best estimate global fit in Riess et al. (2016), and magnitudes are $m_H^W$. We have inverted the normal decreasing magnitude axis used in the literature for presentation purposes

We would now like to feel that we can deduce the distance to any galaxy we can find Cepheids in, by applying this law to convert periods to absolute magnitudes, and comparing to the apparent magnitudes we observe. As is usual, though, things are not that simple! There are three principle objections:

• Are Cepheids in the LMC the same as the ones in distant galaxies? The LMC has a lower metallicity than a typical spiral galaxy, so can we expect the Cepheids found there to have the same brightness? Unfortunately, it is hard to determine the metallicity of a Cepheid from its colour alone, and studies on the effects of metallicity are variable (Ripepi et al. 2020). One might try extending the Leavitt law to add a metallicity term $\kappa$ [Fe/H]. Riess et al. (2019) have estimated Cepheid metallicity in the LMC based on optical spectra of nearby HII regions, and find $\kappa = -0.17 \pm 0.06$, which is consistent with an earlier estimate from Freedman and Madore (2010) that LMC Cepheids are 0.05 mag dimmer than galactic Cepheids, and later results (Gieren et al. 2018; Breuval et al. 2021).

• Is the Leavitt law linear? This matters for $H_0$, because the Cepheids seen in distant galaxies have longer periods than those used to calibrate the Leavitt law: they are brighter and more easily observed at distance. So, $\log {P} \sim 1.5$ for Cepheids in SN Ia host galaxies, whereas the average for the LMC is $\log {P} \sim 0.8$. If the Leavitt law is curved, a bias would be introduced. This can be dealt with by either introducing a separate calibration for short and long period Cepheids, or selecting only long period nearby Cepheids for calibration.

• Can we obtain clean astrometry of very distant Cepheids? We want to observe Cepheids as far away as we can, to maximise the overlap with the SN Ia observations. But pushing the limits of resolution brings the risk of crowding, whereby the Cepheid photometry is blended with nearby dimmer, redder and cooler stars. Indeed, this seems to be the main cause of the increased scatter in residuals for distant galaxies. There are some ways to deal with crowding: Riess et al. (2016) (hereafter R16) add random Cepheids to images of the same galaxy and put them through the same analysis pipeline, to see how well input parameters are recovered. Figure 8 shows an example of this. Cepheids which are outliers in colour, indicative of high blending, may be discarded (removing the colour cut lowers $H_0$ by $1.1 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$). Another way to test for a crowding bias is to look for compression of the relative flux difference from peak to trough (a more blended Cepheid will be more compressed) as is done in Riess et al. (2020). Using an optical Wesenheit magnitude, in which stars may be less crowded than the NIR one, reduces $H_0$ by $1.7 \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (R16), although the argument can be made this is due to higher metallicity effects in the optical (Riess et al. 2019). As with metallicity, the matter of crowding continues to debated.

Fig. 8

Illustration of Cepheid photometry from SN Ia host galaxies from Riess et al (Riess et al. 2016). U9391 is the most distant with a distance modulus of $32.92 \pm 0.06$. The association of Cepheids with spiral arms is clearly visible, and in the bottom left is an example crowding correction for point sources and background flux. The scatter around the Leavitt law is $\sim 0.7$ mag, thought to be due to residual crowding effects

Systematic error analysis is provided in Sect. 4 and Table 8 of R16, where the effect of some different analytical choices such as breaks in the Leavitt law, different assumed values for the deceleration parameter $q_0$, and methods of outlier rejection are shown to be $\pm 0.7\%$. This may not cover all potential systematics. In a recent talk, Efstathiou (2020) re-examined the Leavitt laws of galaxies presented in R16. Calibrating each galaxy individually, the slopes of SN Ia host galaxies are generally shallower than M31 or the LMC, which should not be the case if Cepheids are a single population. A change in the slope will alter the zero-point, as would a change in the distance calibration. It is then noted that forcing the slope of the Leavitt law to $-3.3$ (the M31 value), in combination with using only NGC4258 as the anchor, lowers the R16 $H_0$ value to $70.3 \pm 1.8 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Equation 4.2b). Additionally, there appears to be tension between the relative magnitudes of Cepheids in the LMC and NGC4258, and the distance modulus implied by Masers and DEBs; calibrating with solely the LMC gives a higher $H_0$ value by $4.4 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. It is a feature of $\chi ^2$ fits (as used in R16) that the joint solution will be drawn to the data with the lowest error, which in this case is the LMC value. But if two subsets of the data are in tension, it is uncertain that the one with the lowest $\chi ^2$ would have the least systematics.

Such analyses do not show one value is preferable over another, nor can they show where any discrepancy may lie—it might be metallicity effects, crowded Cepheid photometry, the NGC4258 distance, or some other systematic. Re-analyses of the results of R16 by various authors (Feeney et al. 2018; Cardona et al. 2017; Zhang et al. 2017; Follin and Knox 2018; Dhawan et al. 2018) use the same Cepheid photometric reduction data so are not independent as such.

Research has accelerated to close down these potential issues. We have already mentioned replacing LMC and NGC4258 Cepheids with Milky Way Cepheids in the section on parallax. In a recent paper, Riess et al. (2020) show crowding effects can be detected as a light curve amplitude compression, and that their correction method has been robust. Finally, Javanmardi et al. (2021) fully re-derive the Cepheid periods and luminosities from the original HST imaging for NGC 5584 (which is face-on to the line of sight), intentionally using different analytical choices, finding no systematic difference in the light curve parameters.

All this said, it would be clearly preferable if we had some other candles to check against Cepheids. We now turn to two possibilities, Miras and the Tip of the Red Giant Branch.

3.5 Miras

Miras are variable stars that have reached the tip of the Asymptotic Giant Branch (AGB), comprising an inert C-O core, and a He-burning shell inside a H-burning shell. Their mass is 0.8–8 $M_{\odot }$, although they are typically at the lower end of this range. Their large size of $\sim 1$ a.u. means they are actually brighter by 2–3 mag than Cepheids in the NIR. That they follow a P-L law was first established in 1928 (Gerasimovic 1928), but being tricky to categorise and observe, were not extensively studied until the demand for cross-checks on Cepheids has brought renewed interest in them.

Miras form two distinct populations with O-rich and C-rich spectra, with the O-rich ones exhibiting somewhat less scatter than the C-rich (Feast 2004), but more than Cepheids. Miras have very long periods $90<P<3000$ days and their light curves have many peaks of variable amplitude superimposed (see for example Fig. 3 in Yuan et al. 2017), so investment in observation time is needed to reliably determine P. The P-L law curves upwards at around $P \sim 400$ days, where it seems likely the extra luminosity has been due to episodes of Hot-Bottom-Burning, so an extra quadratic term is required. Miras have high mass loss rates, and the surrounding dust cloud means Wesenheit magnitudes will be less reliable at subtracting reddening compared to Cepheids (because a standard reddening law is assumed in constructing them). Lastly, a size of 1 a.u. would mean their angular diameter is comparable to their parallax, and in addition the photocentre moves around the star, making parallax measurements challenging.

So why bother with them? Their advantages versus Cepheids is that they are (a) more numerous, and, therefore, easier to find in halos where there is less crowding (b) older, so can be found in all types of galaxies including SN Ia hosts with no Cepheids (c) $2-3$ magnitudes brighter than Cepheids in the near infrared. Given imaginative observation strategies and careful population analysis, the issues above can be addressed, and modern studies now exist for Miras in the LMC (Yuan et al. 2017), NGC 4258 (Huang et al. 2018), and the SN Ia host NGC 1559 (Huang et al. 2020).

In the first of the above, Yuan et al. (2017) establish a P-L curve using 600 Miras in the LMC. They have sparse JHK-band observations from the LMC Near Infrared Synoptic Survey (LMCNISS, Macri et al. 2015), which on their own would not be enough to establish the period, but using much denser Optical Gravitational Lens Experiment (OGLE) I-band observations (Szymański et al. 2011), they are able to establish a regression rule for the relationship between passbands, and use OGLE to “fill in” the light curves. The classification of Miras into O-rich or C-rich is also obtained from OGLE. The reference magnitude is defined as the median of maxima and minima of the fitted light curves. The period is obtained by fitting to a sum of sine functions, progressively adding harmonics if supported by a Bayesian Information Criterion.⁷ They fit a law⁸

$$\begin{aligned} M = a_0 + a_1 (\log _{10} P - 2.3) + a_2 (\log _{10} P - 2.3)^2 . \end{aligned}$$

(34)

The K-band for O-rich Miras shows the lowest scatter of 0.12 mag, with $a_0 =-6.90 \pm 0.01$, $a_1 = -3.77 \pm 0.08$, $a_2 = -2.23 \pm 0.2$. The zero-point is obtained using the DEB distance to the LMC given by Pietrzyński et al. (2013). By comparison, the $m_H^W$ scatter for LMC Cepheids obtained by SH0ES was 0.075 mag (Riess et al. 2019) (Fig. 9).

Fig. 9

A PL calibration for Miras in the LMC. While non-linearity can straightforwardly be fitted, contamination must be kept under control. As seen in the bottom three panels, Wesenheit magnitudes have more scatter compared to standard magnitudes (the opposite of applying them to Cepheids), and they also hinder separating O-rich from C-rich stars. Image reproduced with permission from Yuan et al. (2017), copyright by AAS

Huang et al. (2018) observed NGC4258 with the HST WFC in 12 epochs over 10 months. Mira candidates were identified by their V and I amplitude variation, and it was possible to use LMC data to show that using this method contamination between O-rich and C-rich could be kept to a minimum. Their “Gold” sample size was 161 Miras, and fitting Eq. (34) for apparent magnitudes gave $a_0 = 23.24 \pm 0.01$ for F160W with scatter 0.12. Adjusting the ground-based photometry of LMCNISS to F160W equivalent, the authors calculate the relative distance modulus between the LMC and NGC4258 of $\varDelta \,\mu = 10.95 \pm 0.01 \text{(stat) } \pm 0.06 \text{(sys) }$. This is consistent with the Cepheid value of $\varDelta \,\mu = 10.92 \pm 0.02$ (Riess et al. 2016) and the Maser-DEB value of $\varDelta \,\mu = 10.92 \pm 0.041$ (Reid et al. 2019; Pietrzyński et al. 2019). Similar methods are used by Huang et al. (2020) for observations of NGC 1559, with the addition of a low period cut to deal with potential incompleteness bias of fainter Miras. Using the LMC DEB and NGC 4258 distances as calibrators, they obtain $H_0 = 73.3 \pm 4.0 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. So Miras are consistent with Cepheids, but due to their larger error budgets, they are also consistent with Planck results.

3.6 Tip of the Red Giant branch

Red Giant branch stars are stars of mass $\sim 0.5 {-} 2.0 M_{\odot }$ that are at a late stage in their evolution, having moved off the main sequence towards lower temperatures and higher luminosities. The core of the star is degenerate He, and as He ash rains down from the H-burning shell surrounding it, it contracts and heats up. Since the temperature range for He fusion ignition is rather narrow, and the degenerate matter means there is a strong link between core mass and temperature, the core in effect forms a standard candle inside the star, just prior to ignition. As soon as the helium flash ignites, the star moves over the course of 1 My or so (almost instantaneously in stellar evolution terms) to the red clump at a higher temperature and somewhat lower luminosity. Therefore, there is a well-defined edge in a colour-magnitude diagram that can be used to identify the tip of the red giant population just before the flash (TRGB). The TRGB is then not one single star, but a statistical average for a suitably large population.

The TRGB offers many advantages compared to other standard candles. Although red giants are fainter than Cepheids in the optical, in the K-band they are $\sim 1.6$ magnitudes brighter. Stars at or near the TRGB are relatively common, and can be observed readily in uncrowded and dust-free galactic halos. They are also abundant in the solar neighbourhood, meaning great numbers are available for calibration by parallax (by contrast, Cepheids with good parallaxes in Gaia DR3 will number in the hundreds). Sufficient numbers to resolve the tip can be seen in globular clusters such as $\omega$ Centuari, where well-formed colour-magnitude diagrams can resolve metallicity and extinction effects, and an absolute magnitude calibration can be made either from Gaia DR3 parallaxes (Soltis et al. 2021) or DEB distances (Cerny et al. 2021).

Like Miras, they are found in all galactic types. Observation is efficient: one does not need to revisit fields to determine periods. The James Webb Space Telescope is capable of observing red giants in the near IR at distances of $\sim 50 \,\hbox {Mpc}$, which is comparable to Cepheid distances obtainable from the HST.

It is also beneficial that the modelling of late-stage stellar evolution is quite well understood. Empirical calibrations of absolute magnitude and residual dependence on metallicity, mass and age can be checked against the results of stellar codes. For example, the dependency on metallicity is somewhat complex: the presence of metals dims optical passbands by absorption in stellar atmospheres, and brightens the NIR. Serenelli et al. (2017) express the TRGB as a curve with linear and quadratic terms in colour. The authors find an I-band median $M_I^{\mathrm{TRGB}} = -4.07$ with a variation with colour of $\pm 0.08$, and a downward slope in the colour-magnitude diagram as metallicity increases. This median value is consistent with empirical calibrations.

Fitting the TRGB is equivalent to finding the mode of the gradient of the (noisy) stellar distribution in the colour-magnitude diagram, and techniques are borrowed from image processing to do this. The tip has a background of AGB stars, and the edge is sensitive to the distribution of them close to it. If the contamination is large or variable, there is a risk the mode can shift. It is, therefore, important to have a dense population of stars, and enough fields to test the robustness of the fitting process. For example, Hoyt et al. (2021) bin data by separation from the galactic centre and fit the tip separately for each bin.

The Carnegie-Chicago Hubble program (CCHP) have determined TRGB distances for 10 SN Ia host galaxies that also have Cepheid distances, using HST I-band imaging (Freedman et al. 2019). They calibrate the zero point from the TRGB of the LMC and SMC using the DEB distance, finding $M_I = -4.049 \pm 0.022 \;\text{(stat) } \pm 0.039 \;\text{(sys) }$, which is consistent with the theoretical value above (Fig. 10).

Fig. 10

Fitting the TRGB edge from the colour-magnitude diagram of Freedman et al. (2019). The middle panel shows the horizontally-summed (between the blue lines) and smoothed number count, from which the edge is determined by the maximum (vertical) gradient, which is the peak in the right-hand panel. The background AGB population is visible in the stars above the tip

We show in Fig. 11 their comparison of TRGB and Cepheid distances, covering a range of distances from 7 Mpc to almost 20 Mpc. By expanding their sample to non-SN Ia host galaxies, the authors show the TRGB has a lower scatter versus their Hubble diagram than do Cepheids, by a factor of 1.4. Calibrating the Pantheon SN Ia sample on TRGB distances alone gives $H_0 = 70.4 \pm 1.4 \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$, with the difference to SH0ES results due to the TRGB distances to the SN Ia host galaxies being further than Cepheid distances.

Fig. 11

Comparison of TRGB and Cepheid distance moduli, from which it can be seen TRGB distances are consistently larger across a range of galaxies. The red dots are SN Ia host galaxies, the grey dots other galaxies, and the blue star is the LMC TRGB calibrator. Image reproduced with permission from Freedman et al. (2019), copyright by AAS

Currently, this result remains the subject of debate. Yuan et al. (2019) find $M_{I} = -3.99$, which gives $H_0 = 72.4 \pm 2.0 \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. They attribute their result to a different methodology to determine the LMC extinction. Freedman et al. 2019 determine the extinction applicable to the TRGB by comparison of LMC and SMC photometry in VIJHK bands, and using the lower SMC extinction as a reference point. Yuan et al. 2019 adopt the standard reddening law of Fitzpatrick 1999). They also revise the blending corrections of the older, lower resolution photometry of the SMC. Conversely, a calibration of the TRGB in the outskirts of NGC 4258 to the maser distance by Jang et al. (2021) gives a value fully consistent with Freedman et al. (2019). In a followup paper, Madore and Freedman (2020) present an upgraded methodology in which stellar photometry is itself used to separate metallicity and extinction effects (by exploiting their different sensitivities in J, H and K-band magnitudes), confirming their earlier results. Other results (Soltis et al. 2021; Reid et al. 2019; Capozzi and Raffelt 2020; Cerny et al. 2021—see for example Table 3 in Blakeslee et al. 2021) cluster evenly around these two values. We also note the difference between SN Ia zero points (Fig. 6 of Freedman et al. 2019) of the TRGB vs Cepheids appears to increase with distance, and is particularly large for one galaxy, N4308.

More recently, an updated value of $H_0 = 69.8 \pm 0.6 \;\text{(stat) } \pm 1.6 \;\text{(sys) } \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ was published by Freedman (2021). New and updated values for $M_I$ based on the anchors of the LMC, SMC, NGC 4258 and galactic globular clusters are derived. Additionally, potential zero-point systematic problems with the direct application of Gaia EDR3 data to globular clusters (as done by Soltis et al. 2021) are discussed. Each anchor is consistent with each other (although the closeness of the agreement suggests the errors may be over-estimated), and the paper brings the TRGB method on par with Cepheids in terms of number of anchors used.

The TRGB continues to attract attention because the CCHP result is very interesting: it is a late universe distance ladder that is in reduced $2\sigma$ tension with the Planck value of $H_0 = 67.4 \pm 0.5 \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. While it cannot by itself fully resolve the Hubble tension, in combination with some other systematic—perhaps in the calibration of SN Ia (see next section)—it may offer a resolution of it that does not involve new physics.

What is also clear is that quality of a distance ladder is less a matter of quantity of objects, but rather the accuracy of calibration and control of systematics. The TRGB seems very promising, however. Once the calibration is agreed among the community, they offer the tantalising prospect of either confirming the $H_0$ tension through two independent data sets, or reducing it to a lower statistical significance.

3.7 Type Ia supernovae

It is hard to overstate the impact of Type Ia supernovae in cosmology. At $M \sim -19$, they are both bright enough to be seen well into the Hubble flow (the furthest to date is SN Wilson at $z = 1.914$), and have a standardisable luminosity. The mainstream view is that they originate from the accretion of material from a binary companion onto a carbon-oxygen white dwarf. When the white dwarf reaches the maximum mass that can be sustained by degeneracy pressure, the Chandrasekhar mass $M_{\mathrm{ch}} = 1.4 M_{\odot }$, a runaway fusion detonation occurs destroying the white dwarf. Approximately $\sim 0.6 M_{\odot }$ fuses into heavier elements during the first few seconds of the explosion, and the observed light curve, which peaks at $\sim 20$ days and lasts for $\sim 60$ days is powered by radioactive decay of $^{56}$Ni to $^{56}$Co and then to $^{56}$Fe. Hence, a SN Ia is a “standard bomb”, primed to explode when it reaches critical mass.

However, there is surprisingly little observational evidence to confirm the accretion theory. Both the lack of H lines and computer modelling suggest the donor star should survive the explosion, but a search of the site of the nearby SN2011fe both pre- and post- explosion have revealed no evidence of a companion. This may support an alternative “double degenerate” theory that some, or all, SN Ia originate from the merger of two white dwarves (for a review, see Maoz et al. 2014). But if that is the case, why are their luminosities so uniform? Whether SN Ia have one or two types of progenitors has important implications for the Hubble constant, which we return to shortly.

Individual SN Ia luminosities can vary by up to a factor of 2, but they are empirically standardisable by the Tripp estimator (Tripp and Branch 1999):

$$\begin{aligned} \,\mu = m_b - M_{\mathrm{fid}} + \alpha x - \beta c + \varDelta _M + \varDelta _B, \end{aligned}$$

(35)

where $\,\mu$ is the distance modulus, $m_b$ ia the apparent AB magnitude, and $M_{\mathrm{fid}}$ is the absolute magnitude of a typical SN Ia. The parameter x is the “stretch” of the light curve, which is a dimensionless measure of how long the bright peak of the light curve lasts: longer duration SN Ia are brighter. c is a measure of colour: redder SN Ia are dimmer. $\varDelta _M$ is a correction for the environment of the SN Ia, and $\varDelta _B$ a statistical bias correction for selection effects, analogous to the LKH bias of parallax we described earlier. $M_{\mathrm{fid}}$ can be calibrated by finding SN Ia in galaxies for which there are Cepheid or TRGB luminosity distances, or in the inverse distance ladder approach by combination with angular diameter distances from baryon acoustic oscillations, or the CMB.

SN Ia are rare events: approximately 1 per galaxy per century, but by scanning a reasonably sized patch of sky, supernova surveys can detect hundreds per year.⁹ Hence, supernovae catalogs are not uniformly distributed on the sky. However, SN Ia close enough to calibrate their magnitudes are few: there are just 19 SN Ia in galaxies with Cepheid distances from HST observations, although more are expected soon from new cycles (see for example HST proposal 16,198).

To maximise statistics and sky coverage, it is common to use SN Ia from multiple surveys in cosmological analyses. Scolnic et al. (2018) have compiled the Pantheon sample of 1,048 SN Ia from CfA, CSP, PS1, SDSS, SNLS and HST surveys in a uniform light curve calibration, representing almost 40 years of observational data. The sample divides into 180 mostly older Low-z ($z < 0.1$) SN Ia which are uniformly distributed on the sky, and 868 recent High-z SN Ia concentrated in the survey fields, notably the thin “Stripe 82” along the celestial equator. The sets have a small overlap at $z \sim 0.1$, and cross-checks on their spectral and other parameters show they are likely to be from the same underlying population (that is, High-z SN Ia are not intrinsically different to Low-z). However, the mean values of light curve parameters like stretch and colour do drift with z, possibly due to selection effects or changes in the host galaxy properties at higher redshift. Large numbers of Type Ia supernova have also been found, or are in the process of being surveyed, by the Dark Energy Survey (Abbott et al. 2019), All-Sky Automated Survey for Supernovae (Holoien et al. 2018), Foundation Survey (Jones et al. 2019), and Zwicky Transient Facility (Yao et al. 2019).

The process of fitting a SN Ia lightcurve is straightforward. ugriz photometry is corrected for the background sky obtained from imaging the site after the nova has faded (a bonus of SN Ia being transient), and the light curve is fitted to a template, outputting the parameters x, c and $m_b$. However, the bias correction $\varDelta _B$ is challenging and subtle: it depends on the astrophysical modelling of sources of scatter and contamination by mis-classified supernovae, and the selection function of survey. For example, more distant SN Ia may be preferentially targeted for spectroscopic confirmation when their host galaxy is faint, so if their luminosities do depend on the galactic environment, this could bias the High-z population relative the to Low-z. The selection function of early Low-z surveys are not easy to model, and their biases can be up to 0.06 magnitudes. This could account for a somewhat elevated scatter of Pantheon residuals around $z \sim 0.1$ in the Hubble diagram where the two sets join (Fig. 12). After fitting $\alpha$ and $\beta$, the residual intrinsic scatter of the SN Ia population is $\sigma _{\mathrm{int}} \sim 0.1$ magnitudes, which compares favourably with other standard candles.

Fig. 12

Pantheon SN Ia distance moduli and residuals versus a best fit ${\varLambda} {\text{CDM}}$ cosmology. Image reproduced with permission from Scolnic et al. (2018), copyright by AAS

We return now to the question of whether SN Ia have additional environmental correlations that affect their luminosity (that is, what the nature of the $\varDelta _M$ term in Tripp estimator is), and why this may matter for $H_0$. It is generally accepted that SN Ia in galaxies with stellar mass $M_{*} > 10^{10} M_{\odot }$ are intrinsically brighter by $\varDelta _{M,*} \sim 0.04 - 0.06$ than those in lower mass galaxies, and that the transition is sharp, rather than a gradual evolution (see Smith et al. 2020 and references therein). It has, therefore, become common to use a step-function for $\varDelta _{M,*}$ in fits for $H_0$. Riess et al. (2016) calculate the effect is to lower $H_0$ by 0.7%, as the mass of the calibrator galaxies is slightly lower than the mass of the Hubble flow set. The key point is then this: given that Cepheids are young, bright stars formed in active galaxies, is $\varDelta _{M,*}$ sufficiently discriminating to ensure the 19 supernovae in galaxies with Cepheid distances are representative of the thousands in the Hubble flow?

Host galaxy mass itself cannot matter to an individual SN Ia, so it must be a proxy for some other environmental condition. Metallicity does vary with galactic mass, but the step-like feature suggests a connection with star formation: galaxies with mass below the threshold tend to be active, whereas those above are mostly passive. One hypothesis is that there is a prompt/bright SN Ia type that is continuously renewed by star formation, and an delayed/dimmer type originating from stars formed when the galaxy was young (Rigault et al. 2015, 2013; Maoz et al. 2014). But any link between this and SN Ia formed by accretion onto or mergers of white dwarfs is speculative. Also, with estimates of “global” properties being effectively light-weighted, they are biased to galactic centres rather than the outskirts where most supernovae are seen.

If some SN Ia are associated with sites of star-formation, we can expect a better proxy to be local specific star formation rates (that is, star formation normalised by local stellar mass or LsSFR for short), on the grounds that the younger SN Ia population will not have had enough time to disperse from their birth region. Because the pixel resolution of typical SN Ia surveys can resolve a 2 kpc aperture only out to $z \sim 0.1$, studies concentrate on the Low-z sample. Star formation can be estimated from photometry, but is best tracked by $\hbox {H}_{\alpha }$ lines from ionised gas or UV imaging, when available.

Rigault et al. (2020) have examined 141 SN Ia from the Nearby Supernova Factory sample (which has high resolution spectroscopy) and find a significant correlation between LsSFR and $\alpha$, the stretch slope, and no correlation for $\beta$. This suggests there is indeed an intrinsic difference between SN Ia originating in active areas versus passive ones. The size of the LsSFR step is $\varDelta _{M,LsSFR} = 0.163 \pm 0.029$ mag, and including it in the Tripp luminosity estimator eliminates the need for a further global host mass step. The size of the step is interesting as it is significantly larger than $\varDelta _{M,*}$, and because most SN Ia in the Cepheid calibrators are in regions of high LsSFR, whereas in the rest of the Low-z sample the fraction is about a half. Hence, a potential bias to $H_0$ could be as much as 3%. In contrary results, Jones et al. (2018) find a local stellar mass step the same size as $\varDelta _{M,*}$ and little effect on $H_0$, and Riess et al. (2016) found just $0.1 \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ difference in their $H_0$ calculation after restricting to SN Ia found in spiral galaxies. In a recent paper, Brout and Scolnic (2021) argue the true factor is host galaxy extinction (correlated to star formation and hence mass), and present evidence of a distribution separated by colour into blue “clean” SN Ia with lower scatter than their red “dusty” counterparts. The host mass step is absent in the blue sample, and they suggest to use solely these in cosmological analyses to avoid bias (another possibility is to use near-infrared photometry; Dhawan et al. 2018).

In summary, while there is strong evidence SN Ia depend on local specific star formation rates, there is not yet a consensus on the cause, whether they constitute one or two populations, and the level of bias (if any) to $H_0$. They are numerous and, therefore, high relative precision beyond $z>0.1$, and have been dubbed the “guard rails” of the Hubble diagram. However, their absolute accuracy in distance ladders is limited by the small numbers available to calibrate their luminosities, and some uncertainty about the underlying astrophysics. Work is underway to address both of these issues: for example, the Foundation and Zwicky Transient Facility surveys (Jones et al. 2019; Yao et al. 2019) are targeting a new high-quality Low-z set with local spectroscopy to test environmental effects or extensions to the Tripp estimator. New HST observation cycles aim to extend the number of Cepheid calibrators up from 19, and the JWST will access a greater volume, perhaps increasing the calibration set beyond a hundred for both TRGBs and Cepheids. This would make a 1% calibration from at least two independent sources achievable.

3.8 Time delay of lensed quasars

Quasars are bright and can be variable on short timescales. Some are seen to be gravitationally lensed by a foreground galaxy, and each image will have a time delay caused by the extra path length and the gravitational time dilation of general relativity:

$$\begin{aligned} \varDelta t_i = D_{\varDelta t}\left[ \frac{1}{2} (\mathbf {\theta _i} - \mathbf {\beta })^2 - \psi (\mathbf {\theta _i}) \right] , \end{aligned}$$

(36)

where $\mathbf {\theta _i}$ is the sky position of the image, $\mathbf {\beta }$ the (unknown) source position, and $\psi (\mathbf {\theta _i})$ the potential of the lensing galaxy integrated along the line of sight. The relevant quantity for $H_0$ in the above equation is

$$\begin{aligned} D_{\varDelta t} \equiv (1+z_l) \frac{D_l D_s}{D_{ls}} \propto H_0 ^{-1} , \end{aligned}$$

(37)

where $D_l, D_s, D_{ls}$ is the angular diameter distance to the lens, source, and between the lens and the source, respectively, as specified by Equations (11, 14)—in the case of $D_{ls}$ the integration would be done between the redshifts of the lens and source. Then, if we have a system with multiple images, the relative time delay $\varDelta t_{ij} = \varDelta t_i - \varDelta t_j$ of the quasar variability between the images scales with $H_0^{-1}$. The proportionality follows from Eqs. (11, 14) with a weak dependence on other cosmological parameters. Acquiring the time delays $\varDelta t_{i}$ requires extensive observations: relative delays range from weeks to a few months. Errors are typically $\sim 6\%$, although these are reducing over time. A typical lensing system may have $z_s \sim 1.5$ and $z_l \sim 0.5$, so we are probing intermediate cosmological distances.

Each single lens system may provide an independent estimate of $H_0$. But to do so, we need an idea of the lensing potential $\psi (\mathbf {\theta _i})$ above. There is also a tricky degeneracy to deal with, known as the mass sheet transformation. For our purposes, it is sufficient to understand that the same observed time delays may be produced by simultaneously scaling the line-of-sight surface density $\varSigma (\mathbf {\theta })$ of the lensing system by a constant factor $\varSigma (\mathbf {\theta })\rightarrow \epsilon \varSigma (\mathbf {\theta })$ (the “mass-sheet”) and $H_0 \rightarrow \epsilon H_0$. For a clear account of the details, see Falco et al. (1985).

The ingredients for modelling are then this: (a) a range of plausible mass profiles for the lensing galaxy with associated nuisance parameters to be marginalised over (b) a way to deal with the mass sheet degeneracy, through independent constraints on the mass distribution of the lensing galaxy and along the line-of-sight.

This is a challenging, time-consuming and model dependent process for each system! Some other choices must be made, such as which of the galaxies along the line of sight will be modelled and which will be absorbed into the line of sight mass average (Chen et al. 2019). Galactic stellar velocity dispersions provide information on the lensing potential, but as a function of which galactic mass profile is assumed, and with an anistropy nuisance parameter. Also, the accuracy of velocity dispersions at such distances are $\sim 10\%$. If there are visible background galaxies, they may also be lensed and the shape distortions provide extra information on the mass profile. The line of sight mass may be estimated from the density of foreground galaxies, by searching in computer simulations of large scale structure for similar lines of sight, and calculating the line of sight density from them (lenses are associated with over-densities and, therefore, focusing is more likely). But a major advantage is that this modelling can be done blind to final value of $H_0$, eliminating the risk of confirmation bias on the part of the experimenter.

The H0LiCOW team have analysed six such systems so far (Wong et al. 2020), and we show their results below. The main contributions to the errors are uncertainty in the time delay, and velocity dispersion of the lens. H0LiCOW use flat priors of $\varOmega _{M} \in (0.05, 0.5)$ and $H_0 \in (0,150) \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$, to avoid any dependence on other cosmological datasets (although they do assume a flat universe). The results are:

Lens name	$D_{\varDelta t}$ (Mpc)	$D_l$ (Mpc)	$H_0\;(\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1})$
PG1115+080	$1470^{+137}_{-127}$	$697^{+186}_{-144}$	$81.1^{+8.0}_{-7.1}$
RXJ1131-1231	$2096^{+98}_{-83}$	$804^{+141}_{-112}$	$78.2^{+3.4}_{-3.4}$
HE0435-1223	$2707^{+183}_{-168}$	-	$71.7^{+4.8}_{-4.5}$
WFI2033-4723	$4784^{+399}_{-248}$	-	$71.6^{+3.8}_{-4.9}$
B1608+656	$5156^{+296}_{-236}$	$1228^{+177}_{-151}$	$71.0^{+2.9}_{-3.3}$
SDSS1206+4332	$5769^{+589}_{-471}$	$1805^{+555}_{-398}$	$68.9^{+5.4}_{-5.1}$

Their combined result is $H_0 = 73.3 \pm 1.8 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$, a final error budget of 2.4%. However, a key assumption in the combination is independence, and there are many modelling features in common between the lenses, in particular the specific mass profiles used. There is also an apparent drift in $H_0$ values with lensing distance, although the statistical significance is not strong enough to say this is not just random chance.

A re-analysis has been undertaken by the TD Cosmo team (Birrer et al. 2020). By treating the mass sheet degeneracy as a fully unknown parameter at the population level, their analysis reduces reliance on specific mass profiles. For same set of systems, they find $H_0 = 74.5^{+5.6}_{-\,6.1} \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. The central value is consistent with H0LiCOW, but the wider confidence intervals reflect the greater freedom allowed on lens mass distribution, combined with the small number of time-delay lenses. To re-narrow the uncertainty range, the paper investigates what effect introducing a set of non-time delay lensing systems from the SDSS survey may have. The purpose of this larger set is to use their imaging to constrain the mass-profile of lensings galaxy, on the assumption they are drawn from the same parent population as the H0LiCOW sample. TD Cosmo then find $H_0 = 67.4^{+4.1}_{-\,3.2} \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. However, the H0LiCOW sample is selected as those systems capable of producing a clear time-delay signal, which may not have the same characteristics as those selected as having clean shear images. So the assumption they share the same mass profile as each other may not be valid.

It is, therefore, premature to claim lensed quasars are consistent with either SH0ES or Planck. More data is needed: upcoming surveys by the Vera Rubin Observatory, Euclid and Nancy Grace Roman telescope will result in several hundred new time delay systems being discovered (so improvements in analysis efficiency will certainly be needed!). Adaptive optics can provide spatially resolved velocity dispersions to improve the mass models. TD Cosmo estimate 200 extra systems will be needed to constrain $H_0$ within $1.2\%$, which may be within reach in the next five years.

3.9 Gravitational waves

The gravitational wave signal emitted by the merger of two compact objects can be used as a self-calibrating standard candle. There are now operational detectors at LIGO Hanford and LIGO Livingston in the USA, Virgo in Italy, and KAGRA in Japan, with a further planned LIGO India (Abbott et al. 2020). The detectors measure the strain amplitude of a gravitational wave using laser interferometry to detect the miniscule changes in the length of perpendicular beams as a wave passes by. The purpose of the two sites in the USA is to filter out local seismic vibrations. The wave amplitude is related to the chirp mass ${\mathcal {M}}$ which is in turn derivable from the waveform calculated for a merger. A simplified form of the relevant equations are

$$\begin{aligned} {\mathcal {M}}&= \frac{(m_1 m_2)^{3/5}}{(m_1 + m_2)^{1/5}} \end{aligned}$$

(38)

$$\begin{aligned}&= \frac{1}{G} \left[ \frac{5}{96} \pi ^{-8/3}f^{-11/3}{\dot{f}} \right] ^{3/5} \end{aligned}$$

(39)

$$\begin{aligned} {\mathcal {M}}_z&= (1+z_{\mathrm{obs}}) {\mathcal {M}} \end{aligned}$$

(40)

$$\begin{aligned} h(t)&= \frac{{\mathcal {M}}_{z}^{5/3} f(t)^{2/3}}{d_L} F(\theta , i) \cos {\varPhi (t)} \;, \end{aligned}$$

(41)

where f is the frequency, $m_1$ and $m_2$ the merging masses, $\varPhi (t)$ the phase, and h(t) the measured dimensionless strain of the strongest harmonic (Abbott et al. 2016). The rest-frame chirp mass is redshifted by $z_{\mathrm{obs}}$, and F is a function of the angle between the sky position of the source and detector arms, and the inclination i between the binary orbital plane and line of sight (Arun et al. 2009). Note that as we are measuring amplitude rather than energy flux, $h(t) \propto d_L^{-1}$.

In a loose sense, every wave cycle is a measurement of the chirp mass ${\mathcal {M}}$ as it sets $f, {\dot{f}}$, although in practice the full waveform is fitted. The relative precision is floored by sensitivity of the strain measurement, currently around $5\%$. If the redshift and angles were known, $d_L$ and hence $H_0$ would be determined to the same precision.

When a binary neutron star (BNS) system merges, there is an accompanying burst of light from matter outside the combined event horizon. For this reason, it is known as a “bright siren”. If the flash can be observed, the host galaxy is identified and one can use its redshift in Eq. (41). The event GW170817 was just such a BNS merger (Abbott et al. 2017b). The gravitational wave was measured in Hanford and Livingston, which was enough to locate the sky position to 28 $\text{ deg}^2$ (see next paragraph for how). Given the search region, an optical counterpart was found in NGC 4993 at a distance of $\sim 40$ Mpc.¹⁰ Around 3000 cycles of the wave resolved the chirp mass in the detector frame as ${\mathcal {M}} = 1.197M_{\odot }$ to accuracy of 1 part in $10^3$, consistent with a BNS merger. The main remaining uncertainty is then the inclination angle i. Using a flat prior for $\cos {i}$, Abbott et al. (2017a) obtain $H_0 = 70.0^{+12}_{-8} \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. Hotokezaka et al. (2019) improved this to $H_0 = 70.3^{+5.3}_{-\,5.0} \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ by constraining i with observations of the interaction of the ejecta with the ISM.

For black hole mergers, no optical counterpart is generated, and these are called “dark sirens”. However, it is still possible to constrain $H_0$ using them if a probable redshift can be estimated. To do this, the relative amplitudes and time delay between detectors located around the globe are used to approximately determine the sky position (Soares-Santos et al. 2019). For example, if 3 detectors observe the wave with perfect accuracy, the two independent time delays and three measured amplitudes will in turn determine the two sky position angles, two polarisation amplitudes, and one phase lag between polarisations. Hence, simultaneous detections of an event are essential in narrowing the size of the region on the sky where the source is located. A reasonable prior for $H_0$ will constrain the redshift range, and hence determine a localisation volume. Given a suitably complete galaxy catalog with sufficient sky coverage (the best available currently being SDSS and DES), galaxies within this volume can be averaged over with a suitable weighting to determine a value for $H_0$ (Schutz 1986). Although each individual event is not very accurate, there are many more black hole mergers than neutron star mergers, so the errors are competitive in aggregate. It is also straightforward to mix dark and bright sirens to produce a combined result (Palmese et al. 2020) (Fig. 13).

Fig. 13

$H_0$ posterior distribution for the events GW190814 and GW170814, which was localised to a region in the DES survey footprint containing $\sim 1800$ possible host galaxies. The light and dark blue lines represent the dark approach for each siren, which can be compared to the gray dashed line for GW170814 which was localised to one galaxy by its electromagnetic counterpart. The estimate for this bright standard siren can be improved by the addition of the dark sirens, as shown in dark red line. The posteriors of Planck (Planck Collaboration 2020) and SH0ES (Riess et al. 2019) are shown in purple boxes as a guide. Image reproduced with permission from Palmese et al. (2020), copyright by AAS

As each event’s inclination angle is independent, averaging over N events will improve the errors relative to a single event by a factor of $N^{-1/2}$. The main limiting factor is then detector calibration and sensitivity, which determines the event rates. Work is underway at the LIGO sites to improve this, using quantum engineering techniques such as squeezed light.¹¹ Chen et al. (2018) estimate a 5yr observing run by the upgraded LIGO, Virgo, KAGRA and LIGO India detectors will be enough to measure $H_0$ to $1\%$ precision by 2030.

In summary, the appeal of gravitation waves is that if one believes General Relativity correct, they are self-calibrating systems independent of the distance ladder and with minimal astrophysics input. Event rates and improvements in detector calibration are sufficient to converge to a $\sim 2\%$ precision within the next decade.

3.10 Baryon acoustic oscillations

Baryon acoustic oscillations (BAO) are the relic of density fluctuations propagating in the pre-recombination universe. The baryons in an initial localised seed of overdensity (such as would originate from inflation) are subject to radiation pressure and expand outwards at the speed of sound $c_s$, leaving the dark matter behind. At recombination, temperatures have dropped enough so that protons and electrons can combine to neutral hydrogen and the Thomson scattering rate quickly drops below the Hubble expansion rate. At the drag redshift $z_{\mathrm{drag}}$ shortly after, baryons are released from radiation pressure and the baryon overdensity shell is “frozen in” at a characteristic distance relative to the central dark matter overdensity. This distance

$$\begin{aligned} r_d = \int _{z_{\mathrm{drag}}}^{\infty }\frac{c_s(z)}{H(z)} \mathrm{d}z, \end{aligned}$$

(42)

in comoving coordinates is what is referred to as the sound horizon. As the universe continues to evolve, both the baryon shell and the central dark matter overdensity attract further gravitational infall of matter, forming galaxies. Thus, the sound horizon becomes visible as a characteristic (statistical) physical separation between galaxies. The sound speed $c_s = 1/ \sqrt{3(1+R)}$ depends on the baryon-to-photon ratio with $R = 3 \rho _b/4 \rho _\gamma$. $z_{\mathrm{drag}}$ has weak cosmological dependence, and Planck data gives $z_{\mathrm{drag}} = 1059 \pm 0.3$. The key point is that given a cosmological model, $r_d$ is calculable and its scale is large enough that the evolution of structure from $z_{\mathrm{drag}}$ to $z \sim 1$ is nearly linear. Thus we can compare observations of galaxy clustering in the late universe to $r_d$. Armed with data for $r_d$ we can use Eq. (42) above to solve for $H_0$ in our model.

The theory of measuring BAO was largely worked out by the mid 1990s (Feldman et al. 1994). One assumes galaxies are a Poisson sample of the relative matter density field $1+\delta (\mathbf {r})$ and so

$$\begin{aligned} P({\text{ Volume element }} \delta V {\text{ contains a galaxy}}) = \delta V {\bar{n}} (1+\delta (\mathbf {r})), \end{aligned}$$

(43)

where ${\bar{n}}$ is the expected mean space density of galaxies. It is possible to work either with the two-point correlation function $\xi (\mathbf {r}) \equiv \langle \delta (\mathbf {r}^{'}) \delta (\mathbf {r}^{'}+\mathbf {r}) \rangle$ or equivalently the power spectrum

$$\begin{aligned} P(\mathbf {k}) \equiv \int d^3 r \xi (\mathbf {r}) \exp {(i \mathbf {k}\cdot \mathbf {r})}. \end{aligned}$$

(44)

It might seem preferable to use the power spectrum, as we are looking for a characteristic wavelength, and the modes of the power spectrum are independent if the density field is Gaussian. Also, the galaxy survey footprint in real space becomes an easily understood point spread function in Fourier space. In practice though, because of issues with binning such as cut-offs in Fourier space, most research papers calculate both the correlation function and power spectrum. Adjusting ${\bar{n}}$ above can correct for bias introduced by edge effects of angular and redshift cuts of the survey.

Expanding the power spectrum in spherical harmonics, the monopole determines $d_A^2 H^{-1} (z)$, and the quadropole determines $d_A H (z)$ (Padmanabhan and White 2008) in a given redshift bin centred at z. With $\varDelta \theta$ and $\varDelta z$, the density peak separation transverse to and along the line of sight, we can solve for $d_A$ and H. We start with a mock galaxy catalog constructed in a fiducial cosmology seeded with density perturbations. This is matched to our real data with stretches $\alpha _{\perp }, \alpha _{\parallel }$:

$$\begin{aligned} \alpha _{\perp }&= \frac{d_M(z) r_{d,\mathrm fid}}{d_{M,\mathrm fid}(z) r_d}&\alpha _{\parallel } = \frac{H_{\mathrm{fid}}(z)r_{d,\mathrm fid}}{H(z) r_d} \end{aligned}$$

(45)

$$\begin{aligned} \varDelta \theta&= r_d / d_{M}(z) \end{aligned}$$

(46)

$$\begin{aligned} \varDelta z&= H(z) r_d, \end{aligned}$$

(47)

where $d_M = (1+z) d_A$ is the comoving angular distance. Here $\alpha = \alpha _{\perp }^{2/3} \alpha _{\parallel }^{1/3}$ is the monopole term and $\epsilon = \alpha _{\perp }/\alpha _{\parallel }$ is the quadropole.

There is the suggestion of circularity in this: a random catalog constructed in ${\varLambda} {\text{CDM}}$ (with small scale power suppressed) is then “tweaked” to compare to the real sky to justify ${\varLambda} {\text{CDM}}$. However, this method is essentially perturbative. If the real cosmology is far from the fiducial one, a bias might be introduced, but if it is close it should work well.

A technique called reconstruction is used to sharpen the BAO signal (Eisenstein et al. 2007; Anderson et al. 2012), and we describe it briefly here as we will mention it in Sect. 4, when we discuss modified gravity. The observed positions of galaxies will be somewhat moved from their original positions “on” the sound horizon, due to their subsequent infall towards overdensities. This has the effect of blurring the peak of the correlation function, and reduces precision. Reconstruction reverses the infall in the following way: (a) take a volume and smooth out small scale structure $< 20$ Mpc (b) embed it into a larger scale random structure to remove edge effects (c) estimate the displacement $\mathbf {q}$ of each galaxy by the continuity equation $\nabla \cdot \mathbf {q} = -\delta _{\mathrm{gal}}/b_{\mathrm{gal}}$ where $\delta _{\mathrm{gal}}$ is the fractional galaxy overdensity and $b_{\mathrm{gal}}$ the galaxy bias (d) shift the galaxies by $-\mathbf {q}$ plus an additional shift for redshift space distortions (e) do the same to the mock catalog.

Historically, the first galaxy surveys to report a BAO detection were the Two Degree Field survey (Cole et al. 2005), and the Sloan Digital Sky Survey (Eisenstein et al. 2005), followed by WiggleZ (Blake et al. 2011, 2012) and others. We discuss here results from Baryon Oscillation Spectroscopic Survey (BOSS) (Anderson et al. 2012). BOSS has spectroscopically surveyed 1.5 million luminous galaxies over 10,000 $\hbox {deg}^2$ between $0.2< z <0.7$, with angular separations greater than 62$^{\prime \prime }$ (which is 0.5 Mpc at $z \sim 0.7$). Alam et al. (2017) analyse the BAO signal in Data Release 12. The galaxies are divided into three bins each of redshift and $\cos {\theta }$. From a fiducial cosmology with $h = 0.676$, they find $\alpha = 1.042 \pm 0.016$ after reconstruction. Their result is summarised as a set of three values for $d_m (z_i)$ and $H(z_i) \times r_d/ r_{d,\mathrm fid}$ for $z_i =0.38, 0.51, 0.61$, with precision $\sim 2.5\%$ (Fig. 14).

Fig. 14

A beautiful illustration of the BAO peak in the redshift bin $0.4< z< 0.6$ of BOSS DR12. The left-hand panel shows the power spectrum along and transverse to the line of sight, and the right-hand panel is the two-point correlation function. The anisotropy visible in the graphs breaks the $d_A^2 H^{-1}$ degeneracy. Image reproduced with permission from Alam et al. (2017), copyright by the authors

The construction of mock galaxy catalogs is a key part of this analysis. An important parameter is $b_{\mathrm{gal}}$ which is the (assumed linear) ratio of the galaxy overdensity to the matter overdensity. Constructing a mock galaxy catalog by brute force of N-body simulations is prohibitively expensive. Instead, construction starts with a fast, approximate gravity solver for the matter density field seeded with initial fluctuations, and resolution down to halo size. Galaxies are inserted into the matter halos using the bias ratio, while preserving the two- and three- point correlation functions. BOSS assumed $b_{\mathrm{gal}}$ is constant, but more sophisticated models exist. For example, bias tends to be higher for red galaxies (see for example Zehavi et al. 2011). Attention also needs to be paid to what types of galaxies are being counted: massive luminous galaxies of the type measured by BOSS reside in high density nodes of the cosmic web, whereas emission line galaxies are strung out along the filaments. For further details, see Kitaura et al. (2016). BOSS DR12 uses two independent mock catalogs to mitigate against biases introduced by simulation effects.

BAO in isolation do not constrain $H_0$, but rather the combination of H(z) and the sound horizon $r_d$ described above. To obtain $H_0$, we must either fit a cosmological model with constraints on its density parameters supplied by other datasets (for example SN Ia, CMB, or even the full shape of the matter-power spectrum), or we must supply a prior for $r_d$ (which is often obtained from the CMB, but see also below). We describe three independent results below.

Alam et al. (2017) used ${\varLambda} {\text{CDM}}$ calibrated to a combination of the Planck power spectrum and the JLA sample of SN Ia. They find $H_0 = 67.6 \pm 0.5 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. This value is consistent with the Planck result (Planck Collaboration 2020), but is not independent of it.

Lemos et al. (2019) use a parametric formula for H(z), in conjuction with a WMAP-derived prior for $r_d$ and the Pantheon SN Ia sample, to derive $H_0 = 67.9 \pm 1.0 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. This result is now independent of Planck, and their parametric H(z) allows for deviation from ${\varLambda} {\text{CDM}}$ by separating early and late universe expansion histories.

Addison et al. (2018) use data (almost) independent of CMB in ${\varLambda} {\text{CDM}}$. They determine $\varOmega _m = 0.292 \pm 0.02$ by combining galaxy and Ly$\alpha$ BAO.¹²$\varOmega _r$ is derived from the CMB temperature as measured by COBE/FIRAS and numerous balloon experiments (Fixsen 2009). Setting $\varOmega _k = 0$ determines $\varOmega _{\varLambda } = 1 - \varOmega _m - \varOmega _r$. To get the sound horizon, we now just need the baryon density $\varOmega _b$ (see Eq. (42)). Without using the CMB power spectrum, the best available way to get it is from primordial deuterium abundances. In Big Bang nucleosynthesis (BBN), deuterium is burned to create $^{4}$He, with some uncertainty due to the reaction rate of $d(p,\gamma )^3$He. The reaction rate increases with physical baryon density so [D/H] decreases with $\varOmega _b h^2$. The authors use the primordial [D/H] abundance measured from metal-poor damped Ly-$\alpha$ systems, which is $2.547 \pm 0.033 \times 10^{-5}$. Putting this all together, they derive $H_0 = 66.98 \pm 1.18 \; \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. The only CMB data that has been used is the temperature, and the result corroborates the Planck value.¹³ Repeating the analysis with galaxy data from the Dark Energy Survey (DES) Year 1 produces a consistent result (Abbott et al. 2018).

These results are consistent with more recent ones. DES Y3 survey data has been used to derive a set of three correlation measures (referred to as “3x2pt”). These measure the angular correlation of galaxy positions with each other, with the tangential shear of their shapes caused by weak lensing, and the cross-correlation in the two components of their ellipticities also due to weak lensing. Combining this with Planck, SN Ia data, BAO and redshift space distortions, the DES Collaboration (Abbott et al. 2021) find $H_0 = 68.0^{+0.4}_{-\,0.3} \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ when fitting to the ${\varLambda} {\text{CDM}}$ model. The eBOSS survey, the culmination of more than 20 years of survey work at the Apache Point Observatory, find $H_0 = 68.19 \pm 0.37 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ when fitting to a ${\varLambda} {\text{CDM}}$ model using their data plus the above additional probes to also fit to ${\varLambda} {\text{CDM}}$ (Alam et al. 2021). These seem to be the tightest constraints on $H_0$ yet published.

We also note that the logic explained above to derive $H_0$ can be reversed: BAO can be combined with a $H_0$ prior from nearby universe results, instead treating the sound horizon $r_d$ as a free parameter (Bernal et al. 2016). The $r_d$ values so inferred are in tension with the CMB, and we return to this point in Sect. 4.2.

In summary, BAO serve as a standard ruler in the late universe which are almost independent of astrophysical assumptions. They may be used in extended models beyond ${\varLambda} {\text{CDM}}$, albeit with the caveat they have been derived perturbatively against a ${\varLambda} {\text{CDM}}$ background simulation. The two main data sets of BOSS and DES are soon to be joined by others. The Dark Energy Spectroscopic Instrument is operational, the ESA survey satellite Euclid is scheduled for launch in 2022 which is also when science operations on the Vera Rubin Observatory LSST in Chile commence. All of these surveys are complementary and will increase the precision and range of BAO measurements. Combined with deuterium abundances, BAO are an important corroboration of the Planck and WMAP results for $H_0$.

3.11 Cosmic microwave background

The CMB power spectrum carries the imprint of the same acoustic oscillations we described for BAO, sampled on the surface of last photon scattering. The Planck 2018 value of $H_0 = 67.4 \pm 0.5 \; \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Planck Collaboration 2020) is notable for its precision, and is consistent with previous results such as Boomerang $64 \pm 10 \; \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Percival et al. 2002) and WMAP $70.0 \pm 2.2 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Hinshaw et al. 2013). More recently, the Atacama Cosmology Telescope (ACT) finds $67.9 \pm 1.5 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Aiola et al. 2020). There is, however, a moderate tension between Planck and the South Pole Telescope (SPT) result of $71.6 \pm 2.0 \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$, and the origin of the difference is not yet clear (Henning et al. 2018; Handley and Lemos 2021).

Two questions are immediately raised: how is $H_0$ derived from a power spectrum sampled on the two-dimensional sky of the early universe, and why is the Planck value so precise?

To answer the former, we need to explain how the CMB power spectrum determines cosmological parameters. The spectrum is created by primordial fluctuations that evolve as a function of their scale and the sound speed, until recombination. Whilst this radiation is highly isotropic, we can obtain cosmological results from measurements of small anisotropies in both the temperature and the polarization of CMB photons. The former of these provides the largest amount of cosmological information, and can in fact measure the Hubble constant at high enough accuracy to be in tension with direct measurements without relying on polarization. These temperature anisotropies ($\varDelta T \equiv T(\mathbf {n}) - T_0$) can be expanded in a basis of spherical harmonics:

$$\begin{aligned} \varDelta T (\mathbf {n}) = \sum _{\ell =0}^{\infty } \sum _{m = - \ell }^{\ell } a_{\ell m} Y^{m}_{\ell } (\mathbf {n}) . \end{aligned}$$

(48)

The power spectrum of the coefficients is commonly expressed as ${\mathcal {D}}_{\ell } = \ell (\ell +1) C_{\ell }/ 2\pi$, where

$$\begin{aligned} C_{\ell } \equiv \frac{1}{2\ell +1} \sum _{m} a_{\ell m} a_{\ell \, -m} \end{aligned}$$

(49)

is the estimator of the power spectrum (we have only one CMB, so averaging over m is a way to estimate the true “universe average” we want). The spectrum is shown in Fig. 16 and contains all the statistical information of the temperature anisotropies, as long as these are Gaussian (no evidence supporting non-Gaussianity in the CMB has been detected at the time of writing). This power spectrum has three main features:

• Large-scale plateau at scales ($\ell < 100$) that are not affected by post-recombination physics, and, therefore, reflect the primordial power spectrum. As noted above, we have just one “sampling” of the random seeds, so the amount of information we can extract from low multipoles is limited by cosmic variance $\propto (2\ell +1)^{-1/2}$.

• Acoustic oscillations which depend on the sound horizon size

  $$\begin{aligned} r_s(z_\star ) = \frac{1}{H_0 \varOmega _m^{1/2}} \int _{0}^{a_\star } \frac{c_s}{\sqrt{a+a_{\mathrm{eq}}}}\mathrm{d}a \end{aligned}$$

  (50)

  in flat ${\varLambda} {\text{CDM}}$ where $a_{\mathrm{eq}} = \varOmega _r / \varOmega _m$, $\varOmega _b h^2$ determines $c_s$ and both determine $a_\star = a(z_\star )$, the scale factor at the surface of last scattering. These create the peaks in the spectrum.

• Silk damping which is photon diffusion from hotter regions to colder ones, suppressing small scale power (Silk 1968). The mean free path of a photon is $\lambda = 1/(\sigma _T n_e)$ where $n_e$ is the number density of charged particles and $\sigma _T$ the Thomson cross-section, so photons can diffuse a length $r_{\mathrm{Silk}} = \sqrt{\lambda /H}$. As the sound horizon $r_s \propto 1/H$, then $r_{\mathrm{Silk}}/r_s \propto \sqrt{H/n_e}$. Silk damping creates the downward slope in the spectrum, so this is sensitive to $n_e \propto \varOmega _b$.

With all of this, how does the CMB constrain the Hubble parameter? First, we can measure the acoustic scale length $r_s$, which serves as a standard ruler. As described in Eq.  50, this can be calculated as a function of $\varOmega _r$, $\varOmega _m h^2$ and $\varOmega _b h^2$: The radiation density $\varOmega _r$ is determined by the temperature of the CMB. $\varOmega _m h^2$ can be estimated from the effect of the integrated Sachs–Wolfe effect (Sachs and Wolfe 1967)—the redshift of CMB photons through wells or hills of gravitational potential during eras of non-matter domination—in the low multipoles of the power spectrum. Finally, the relative amplitudes of the acoustic peaks in the CMB serve to measure the ratio $\varOmega _b/\varOmega _m$. Once we have computed the acoustic scale, we need a measurement of its comoving angular diameter distance $\theta _s$, which is given by the distance between the acoustic peaks.¹⁴ In a flat ${\varLambda} {\text{CDM}}$ model, this provides a measurement of the matter density $\varOmega _m$, which combined with the measurement of $\varOmega _m h^2$ gives an estimate on the Hubble parameter. This is illustrated graphically in Fig. 15.

Fig. 15

A schematic of how the sound horizon determines $H_0$. We observe the angular peak spacing $\theta _s$, and calculate $r_s$ from the pre-combination universe given a model for the sound speed and expansion history there. The comoving distance $\chi _s$ is then used to solve for $H_0$ given how $\chi _s$ evolves in the post-recombination universe. The box gives the flat ${\varLambda} {\text{CDM}}$ formula for this. This figure is our version of Antony Lewis’ original at https://cosmologist.info

Planck measured full-sky temperature T and polarisation E fluctuations in 9 frequencies, with angular resolution up to 5 arcmins ($\ell \simeq 2000$) and sensitivity $2 \times 10^{-6}\,\mu$K. Before calculating the TT, TE and EE power spectra, foreground effects must be calculated and removed, and much of the work done by the Planck collaboration between successive data releases has been to develop the foreground model, and reduce the uncertainties it may introduce. Foreground effects include:

• Peculiar velocity of the Earth-Sun system induces a dipole which is easily subtracted. The annual motion of the Earth is actually helpful to calibrate the detector response.

• Galactic synchrotron and free-free emission caused by cosmic rays interacting with the magnetic field and ISM of the MW. This has a non-thermal frequency spectrum (in effect its colour is different to the CMB).

• Galactic dust emission whose contribution to the spectrum is also subtracted by estimating its mapped “colour” difference to the CMB.

• Point sources of microwave emission are masked. Sky masking introduces some correlation between multipoles.

• Sunyaev–Zel’dovich (SZ) effect where CMB photons interact with hot intracluster gas and are Doppler-shifted (the kinetic SZ effect) by bulk motion or up-scattered (the thermal SZ effect) (Sunyaev and Zel’dovich 1972). The former effect does not alter the black-body spectrum, but the latter does. The kinetic SZ effect is sensitive to epoch of re-ionisation at $z \sim 8$ (Planck Collaboration 2014b). The thermal SZ effect may be exploited to produce a cluster map from which information on inhomogeneity can be extracted (Planck Collaboration 2014a). Modelling of intracluster gas predicts a spectral template (which peaks around $\ell \simeq 2000$) to subtract.

• Weak lensing of the CMB by matter. Weak lensing peaks between $1<z<2$, and may be used as a probe of the distribution of foreground matter. The effect increases as we move to smaller scales, particularly $\ell > 2000$ (Zaldarriaga and Seljak 1998). There are two signals of lensing: (a) its non-gaussianity, which can be measured by a four-point correlation function (b) a smoothing effect on the peaks and troughs of the spectrum, both of which can be calculated as a function of $\varOmega _M$. However, there is more smoothing apparent in the spectrum than is predicted by the correlation function so a phenomenological parameter $\varOmega _{m,\mathrm spectrum} = A_{\mathrm{lens}} \varOmega _{m,\mathrm correlation}$ has been introduced to capture their relative amplitude. $A_{\mathrm{lens}} \simeq 1.2 \pm 0.1$ is seen in both Planck and South Polar Telescope (SPT) data (Bianchini et al. 2020), but appears to be absent in the Atacama Cosmology Telescope (ACT) data (Aiola et al. 2020).

The latter two are perhaps better characterised as secondary anisotropies, as they have been used to derive cosmological information in their own right. The secondary anisotropies then provide a consistency check of certain parameters derived from the primary anisotropies, if the modelling is correct. We examine $A_{\mathrm{lens}}$ in greater depth below.

Cross-checks on the effectiveness of foreground modelling are done by switching frequency bands, using alternative astrophysical models, and numerical simulations of parameter recovery from random CMB backgrounds (Planck Collaboration et al. 2016, 2020). The spectrum is then compared to one computed in a standard code such as CMBFAST (Seljak and Zaldarriaga 1996), CAMB (Lewis et al. 2000) or CLASS (Blas et al. 2011) and a posterior for each cosmological parameter is computed. In each check, no serious discrepancy with the main results was found. Although each $C_{\ell }$ individually has $\simeq 7\%$ noise, there are 2000 of them and the error is reduced further by the lensing signal. The binned spectrum and residuals is shown in Fig. 16. We now consider two questions regarding the data.

Fig. 16

The binned Planck power spectrum for TT and residuals to the best fit ${\varLambda} {\text{CDM}}$ model. The vertical line delineates the different methodology used to resolve the power spectrum at $l<30$. Note that the figure shows the power spectrum of the temperature T, not of the anisotropies $\varTheta$. Image reproduced with permission from Planck Collaboration (2020), copyright by ESO

Is Planck self-consistent? A feature which is (barely) visible by eye in Fig. 16 is an oscillating residual pattern lining up to the spectral peaks, indicating the Planck spectrum is slightly tilted versus theory (see Fig. 24 of Planck Collaboration (2020) for an enlarged view). As each multipole is nearly independent, we can split the spectrum and run the analysis on each half. Addison et al. (2016) find that $A_{\mathrm{lens}}$ is equivalent to a drift of cosmological parameters with different scales in the CMB. They fix $A_{\mathrm{lens}} =1$ and compare $H_0$ for $\ell <1000$ and $\ell >1000$ finding $H_0 = 69.7 \pm 1.7 \; \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ and $H_0 = 64.1 \pm 1.7 \; \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$, respectively. Allowing $A_{\mathrm{lens}} = 1.3$, or a tilt parameter restores concordance.

We caution that $A_{\mathrm{lens}}$ is not a physical parameter connected to lensing; it is a “fudge factor” that resolves internal inconsistency in CMB data. It does not resolve the $H_0$ tension, but does resolve matter power amplitude $\sigma _8$ tension with galaxy survey data such as the Dark Energy Survey and Kilo-Degree Survey. Could it be a foreground effect? Its value is relatively stable for various band channels and sky masks, which argues that it is not. The Planck Collaboration followed up on this curiosity (Planck Collaboration 2020). They note a dip in the power spectrum for $l<30$ pulls low-$\ell$ $H_0$ higher; this may account for the lower-resolution WMAP measurement being somewhat higher than Planck. The dip between $1420 \le \ell \le 1480$ mimics lensing but may be an unaccounted foreground effect. Potential explanations such as negative curvature density $\varOmega _k <0$ and modified gravity are investigated but no convincing evidence is found in favour of these models when BAO data are added to the fit. A re-analysis of the Planck data using a different foreground subtraction methodology (Efstathiou and Gratton 2019) found that $A_{\mathrm{lens}}$ decreased from 1.26 to 1.06 as the data were broadened from the temperature-only power spectrum to include polarisation and lensing data. Further, Planck data passes other consistency tests with the baseline ${\varLambda} {\text{CDM}}$ model where A-type parameters may be introduced, such as the expected magnitude of the lensing correlation function and the Sachs–Wolfe effect. Hence, the preferred explanation of the Planck Collaboration is that $A_{\mathrm{lens}}$ is a statistical fluke. Nevertheless, while $A_{\mathrm{lens}}$ does seem to vary over the sky, it is perhaps of concern that it seems to be larger for full-sky Planck data is and is a roughly $2\sigma$ effect.

Is Planck consistent with other current CMB measurements? The SPT covers a $6\%$ patch of the southern sky at a resolution 6$\times$ that of Planck, finding $H_0 = 71.3 \pm 2.1\; \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Henning et al. 2018). SPT is limited to $\ell >650$ due its low sky coverage and atmospheric effects and has greater noise, but when the results are compared on a like-for-like basis (“Planck-in-patch” with SPT for $650< \ell < 1800$), they are consistent with Planck. The analyses are independent and so argue against systematic errors (in this patch and multipole range) in either experiment. However, including higher SPT multipoles in the 150 GHz spectrum causes $H_0$ to drift higher: $H_0 \simeq 74 \pm 3\; \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ for $650< \ell < 3000$ (Aylor et al. 2017). While this is the opposite direction to Planck data, this may be due to the $l<30$ effect in Planck noted above. SPT confirm the Planck result of a greater lensing effect than predicted, and also note a spectral tilt versus the best-fit ${\varLambda} {\text{CDM}}$. However, the trend is not apparent in 143 GHz data, so it is not at all clear if this is a physical effect, rather than merely chance or systematics. The ACT Data Release 4 derives cosmological parameters from a $6,000 \mathrm deg ^2$ patch of the southern sky up to $\ell \sim 4000$, finding $H_0 = 67.9 \pm 1.5\; \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Aiola et al. 2020), however, ACT appears to be in $2.6\sigma$ tension with Planck Handley and Lemos (2021); this appears to be caused by differing physical baryon densities.

In summary, Planck 2018 results for $H_0$ are consistent with previous and current independent CMB data. The high precision for $H_0$ is a consequence of Planck’s high resolution, lack of atmospheric interference, and full sky coverage. Checks have been performed on the codes, the methods used to remove foregrounds, and beam effects. Internal inconsistencies hint at new physics or foreground effects at small angular scales, manifesting either as a tilt or a smoothing of the spectrum, and non-physical parameters like $A_{\mathrm{lens}}$ have been introduced to capture them. However, after their introduction the results for $H_0$ are not materially affected, and remain in tension with late universe results. Nevertheless, the persistence of these effects across differing sky patches, multipole ranges and experiments make them less likely to be a statistical fluke. It is hoped next generation CMB experiments with resolution up to $\ell =5000$ will shed further light on this.

3.12 Other methods

Promising methods that we did not have space to discuss are Surface Brightness Fluctuations (Tonry and Schneider 1988; Blakeslee et al. 2021; Khetan et al. 2021), Cosmic Chronometers (Jimenez and Loeb 2002; Moresco et al. 2018), the Tully–Fisher relation (Tully and Fisher 1977; Kourkchi et al. 2020; Schombert et al. 2020), Type II supernovae (de Jaeger et al. 2020), HII galaxies (Terlevich and Davies 1981; Arenas et al. 2018), and Galaxy Parallax (Croft 2021). Quasars (Risaliti and Lusso 2019) and GRBs (Schaefer 2007) offer the prospect of extending the Hubble diagram up to $z \sim 5$, further testing ${\varLambda} {\text{CDM}}$. However, despite improvements in characterising their intrinsic luminosity from observables (for example X-ray and UV flux in the case of quasars), it remains challenging at present to regard them as standard candles. We refer the reader to the above for the latest work in these fields.

4 Could new physics explain the tension?

We have now reviewed the main recent results on $H_0$, and while in the spirit of scientific scepticism we have identified potential sources of systematic error, we hope it is also clear how much effort has been made to root out potential biases. Therefore, a possibility that should be taken seriously is that the tension is real, and a sign of new physics.

Some authors have interpreted the disagreement between CMB results and Cepheids as “early versus late” tension. In this view, ${\varLambda} {\text{CDM}}$ with its fluids of radiation, standard model neutrinos, cold dark matter, baryons and dark energy is not the right model to derive $H(z=0)$ from the apparent $H(z \sim 1100)$. If late-time physics were changed, $H_0$ derived from the early universe might be reconciled to the local one. Alternatively, a change to pre-recombination physics would alter our calculation of the sound horizon $r_s$, and hence we would need to change distances to retrieve the same angular sizes of the CMB temperature fluctuations. More radically, some authors have argued our local $H_0$ is different from an average over randomly placed observers.

The essential problem for model builders is this: in other respects, ${\varLambda} {\text{CDM}}$ fits the data very well across a huge span of the history of the universe. The CMB is not merely a “snapshot” of the universe, but carries the imprint of several epochs. The positions and heights of the peaks are sensitive to the content¹⁵ between $z \sim 10^5$–$10^3$, the high-$\ell$ slope depends on the baryon-to-photon ratio close to recombination at $z \sim 1100$, and CMB lensing by matter peaks between $z \sim 1$–2. At earlier times, ${\varLambda} {\text{CDM}}$ makes an accurate prediction of primordial element abundances, especially deuterium. At late times, galaxy surveys are consistent with the evolution of perturbations in a ${\varLambda} {\text{CDM}}$ background,¹⁶ and place tight limits on deviation from spatial flatness in the mid to late universe. The shape of H(z) can be read off SN Ia luminosities between $0.01< z < 1.4$, and is also consistent with ${\varLambda} {\text{CDM}}$.

What we want to have is a model capable of modifying $H_0$ by the right amount, without disrupting ${\varLambda} {\text{CDM}}$’s other successful predictions. The model must be testable, compatible with particle physics results, and ideally not fine-tuned. Two serious problems must be avoided: by dint of extra parameters, most models increase the range of allowed $H_0$ values. When a prior of $H_0$ from the local universe is convolved with the expanded likelihood, the posterior will—by construction—overlap with the prior. So to claim a resolution of the Hubble tension in this way is to use the same data twice: once to construct the posterior, and once to compare it. This can be avoided if the extra parameters have some preferred values—for example, a range that is predicted by microphysics (Vagnozzi 2020). A second problem with the use of $H_0$ priors has been discussed by Efstathiou (2021), who points out the difference between it and the actual data analysis performed by the SH0ES team, which is a calibration of the SN Ia fiducial absolute magnitude $M_B$, followed by a conversion from $M_B$ to $H_0$. To use an $H_0$ prior is then to transform and compress the data away from its true source; it would instead be better to use $M_B$ directly and priors for this are given in Camarena and Marra (2021). Another prevalent issue is the selective use of datasets—in particular, BAO provide strong constraints on the late universe as we shall see shortly, and to omit them is again to risk a misleading analysis.

A large number of creative proposals have been put forward, so much so that unfortunately we do not have space to introduce them all. Our preference here is to review selected models in broad classes that we hope will be informative, and readers are referred to extensive reviews by Mörtsell and Dhawan (2018), Knox and Millea (2020), Di Valentino et al. (2021), and Vagnozzi (2020) if they would like more detail.

4.1 Late-universe physics

In some respects, it is easier to propose changes to the late universe: one does not have to “negotiate” with the CMB power spectrum! It is straightforward to generalise the expansion history into any number of “cosmology-independent” forms, that do not rely on any specific form of matter-energy, or general relativity: all that is retained are the Copernican principles of homogeneity and isotropy, and the existence of a space-time metric (for example, see Eq. (15)). The latter is important, as it implies the Etherington relation: $d_L = (1+z)^2 d_A$, which locks angular diameter distances against luminosity distances.

4.1.1 Modified gravity

Traditional models of large-scale modified gravity (normally referred to as MOND) would seem to have a low chance of solving the Hubble tension; the success of using reconstruction to sharpen the BAO peak argues that standard gravity works as we expect on these scales. Desmond et al. (2019) have proposed that small-scale modified gravity could distort the calibration of Cepheids in large galaxies like the Milky Way and NGC4258, however, this appears to be disfavoured by the fact that using the LMC as a sole calibrator does not materially change $H_0$.

4.1.2 Inhomogeneities and redshifts

Clearly our universe is not completely uniform, so could we by chance live in an underdense region, measuring a local $H_0$ above the universal one?

Shanks et al. (2019) have investigated the “local hole” idea, initially noted in galaxy survey data by Keenan et al. (2013). They cite peculiar velocity outflows from $0< z < 0.1$ in the 6dFGS galaxy survey as evidence for a local underdensity, finding the universal (i.e. CMB) $H_0$ to be lower than our local one by 1.8%. However, we would expect to see the effect of a line of sight exiting our underdense region as a kink in the residuals of SN Ia luminosities fitted to ${\varLambda} {\text{CDM}}$, or alternatively as an anistropy in $H_0$ depending on the footprint of the SN Ia survey used. While the sky distribution of low-z SN Ia versus Hubble flow SN Ia are very different, and there is an uptick in magnitude residuals on the boundary between the two (see for example Fig. 11 of Scolnic et al. 2018), the lack of evidence for such a kink places limits on any local under-density (Kenworthy et al. 2019). Also, large-scale structure simulations find the probability for us to be in an underdensity of such magnitude is less than 1% (Odderskov et al. 2017; Macpherson et al. 2019) (although a different likelihood of a void may be obtained in a revision of ${\varLambda} {\text{CDM}}$). That said, the observational tension between claims of local under-density based on galaxy surveys, and the lack evidence for it in SN Ia data, remains unexplained.

Density fluctuations also necessitate the adjustment of redshifts for peculiar velocities. Although heliocentric redshifts can be measured up to an accuracy of $10^{-7}$, care is needed in the conversion to cosmological ones. Davis et al. (2019) have analysed the effect of redshift biases on $H_0$. Changing z by $+0.001$ for a set of standard candles between $0.01< z < 0.15$ causes a bias in $H_0$ of $\sim 3\%$. Systematics might arise in peculiar velocity estimates or corrections for residual stellar motion (for example, if observing on one side of a spiral galaxy). Rameez (2019) has pointed out differences between the redshifts for SN Ia in common between the JLA and Pantheon catalogs; there are 58 with differences $>0.0025$, concentrated in an arc opposed to the CMB dipole. Nevertheless, this does not appear to be biasing any $H_0$ estimates.

4.1.3 Modifying late-time ${\varLambda} {\text{CDM}}$

In ${\varLambda} {\text{CDM}}$, dark energy is a property of the vacuum, with equation of state $\rho = wP$ where $w=-1$. This distinguishes it from standard inflation models, where $-1< w < 0$ is a time-varying function of the potential and kinetic energy of a scalar field, but makes its microphysical origin rather obscure. This has caused some theorists to speculate with alternative models.

In principle then, modifying dark energy in the late universe may be considered as a solution. The CMB has little to say about late-time dark energy: at early times, its physical density is much smaller than matter and radiation. The late time Integrated Sachs–Wolfe effect does imprint on the spectrum, but only as a large scale secondary anisotropy once the universe has entered the dark-energy dominated phase at around $z \sim 0.3$.

A simple modification of ${\varLambda} {\text{CDM}}$ would be to allow w to take on an arbitrary (constant) value. However, as what is required is a boost to late-time expansion to match the local universe $H_0$, we would need $w<-1$ (known as phantom dark energy) to solve the tension. Phantom dark energy does not occur in standard single scalar field models, but is possible in models with more complex field configurations. If sustained, phantom dark energy leads to a “Big Rip” in a finite time, where all matter is pulled apart by accelerated expansion of the universe.

Alternatively, dark energy may be considered a late-universe emergent phenomenon by allowing its equation of state to vary with time. This may be done writing $w(a) = w_0 + (1-a)w_a$, or by replacing $\varOmega _{\varLambda ,0}$ in Eq. (12) with a phenomenological $\varOmega (z)$. This could be motivated by the action of scalar fields, dark matter decaying to dark energy, or some other novel microscopic theory of dark energy (see for example Di Valentino et al. 2021). However, it can be shown that such models have a generic problem: the sound horizon. The sound horizon $r_d$ is normally introduced via its definition from early universe physics (Eq. 42). But it is also imprinted on the late-time universe, as the peak in the angular correlation function of galaxy number densities, which constrains the product $r_d H_0$. All that is needed is a late-time distance measurement to convert the angular size to a physical size at a given redshift, SN Ia to constrain the late-time expansion history, and $r_d$ may be calibrated independently of the CMB.

Arendse et al. (2019) have used the H0LiCOW lens distances, BAO and Pantheon supernovae to obtain just such a late-time $r_d$. They show that two modified late-time dark energy models applied to Planck data can resolve its $H_0$ tension with the late-universe, but not its $r_d$ tension. Knox and Millea (2020) investigated this in ${\varLambda} {\text{CDM}}$ with the same result.

Hence, if all data including BAO are considered—as they should be—it appears that late-time modifications to ${\varLambda} {\text{CDM}}$ will not be satisfactory as a solution to the Hubble tension.

Fig. 17

${\varLambda} {\text{CDM}}$ tensions in the $r_d - H_0$ plane. $\omega _m$ is the physical matter density $\varOmega _m h^2$ and $r^{drag}_{s} \equiv r_d$ is the sound horizon from the end of the baryon drag epoch. There is no combination of values in standard, flat ${\varLambda} {\text{CDM}}$ that can explain observations. Image reproduced with permission from Knox and Millea (2020), copyright by APS

4.2 Early-universe proposals

We have mentioned how the CMB is a set of rulers whose scale is fixed at different epochs. To recap, the observed angular scale of the sound horizon at a given redshift z is

$$\begin{aligned} \theta (z) = \frac{r_s}{d_A} = \frac{\int _{z_D}^{\infty } \frac{c_s (z') dz'}{H(z')}}{ \frac{1}{1+z} \int _{0}^{z} \frac{dz'}{H(z')}} \;, \end{aligned}$$

(51)

where $c_s(\omega _b,z)$ is the sound speed which depends on the physical density of baryons, given by $\omega _b = \varOmega _b h^2$. Decoupling happens when the mean free path of photons approaches the Hubble radius c/H(z), hence $z_D$ is also a function of all of the densities $z_d \equiv z_d(\omega _{b}, \omega _{m}, \omega _{\gamma })$. Loosely, the goal is to reduce the sound horizon from (42) by $\simeq 7\%$, as shown in Fig. 17.

We may isolate the free parameters of this formula, from those that are fixed by data as follows. As discussed, we may omit dark energy $\omega _{\varLambda }$ in the numerator. In the late universe the radiation density is not significant, and using the spatial flatness implied by BAO, we may write $\varOmega _{\varLambda } = 1- \varOmega _m$.

$\varOmega _m$ is determined by the heights of peaks in the CMB spectrum. Successive peaks represent modes that have crossed the horizon successively earlier in the universe when the ratio of matter to radiation was lower, and so will have had their growth suppressed by radiation pressure to a greater degree. $\varOmega _m$ determined in this way from the CMB is consistent at a variety of redshifts with values from the late universe: Lyman$-\alpha$ absorption lines of quasars, BAO, galaxy lensing and the SN Ia Hubble diagram (see Fig. 3).

Further, $\varOmega _b$ is determined by the Silk damping of high-$\ell$ modes, and also by the relative heights of odd and even peaks: these are, respectively, compression and rarefaction modes, sensitive to the pressure to density ratio. $\varOmega _b$ from the CMB is consistent with the deuterium fraction predicted by BBN. Then, substituting for H(z) using (7), Eq. (51) becomes

$$\begin{aligned} \theta (z) = \frac{\int _{z_D(\omega _b, \varOmega _m h^2)}^{\infty } \frac{c_s (\omega _b, z') dz'}{[(1+z')^3 + \frac{\omega _r}{\varOmega _m h^2}(1+z')^4]^{1/2}}}{\frac{1}{1+z}\int _{0}^{z} \frac{dz'}{[\frac{1-\varOmega _m}{\varOmega _m} + (1+z')^3]^{1/2}}} \;. \end{aligned}$$

(52)

Hence we see that for fixed $\omega _b$, $\omega _r$ and $\varOmega _M$—all parameters whose CMB values are corroborated by non-CMB datasets—h only appears in the numerator. So to change $H_0$ we must either accept a departure from the Friedmann equations, change $\omega _r$, allow conversion between energy types, or add a new non-baryonic, non-dark matter component to the mix of the early universe.

4.2.1 Extra relativistic species

Extra relativistic species, such as additional neutrinos beyond the Standard Model flavours, are well-motivated in extensions to the standard model in particle physics. There is a well-known constraint of 3 on the number of light neutral particles from the decay width of the Z-boson, but this bound may be avoided if the new particles do not couple to the Z (for example, if they are sterile neutrinos which only interact gravitationally). The number of species are parametrised by $N_{\mathrm{eff}}$ which is defined by

$$\begin{aligned} \omega _r = \{ 1+ N_{\mathrm{eff}} \frac{7}{8} (\frac{4}{11})^{4/3}) \} \omega _{\gamma } \;, \end{aligned}$$

(53)

where the fractions are due to the fermionic nature of neutrinos, and in the standard model $N_{\mathrm{eff}} = 3.045$.¹⁷ Adding extra species would mean $H_0$ in Eq. (52), would need to be increased to keep $\theta$ unchanged (Bernal et al. 2016).

But if we increase $\omega _r$, we have altered the redshift of matter-radiation equality $z_{\mathrm{eq}}$ which influences the relative heights of the peaks. If we restore the heights by also increasing $\varOmega _m$ to keep $z_{\mathrm{eq}}$ unchanged, we conflict with $\varOmega _m$ determined from SN Ia, BAO and lensing unless we accept dark matter decay between the CMB and then. Additionally, $N_{\mathrm{eff}}$ is constrained by He abundance to be $<4$ at the $3\sigma$ level during BBN (Aver et al. 2015) (see also Fig. 39 in Planck Collaboration 2020).

One way in which these constraints can be avoided is via self-interacting neutrinos. The new species couples to itself, but not the standard model neutrinos (although it mixes with them). Free streaming neutrinos have a small but measurable impact on the spectrum as they travel faster than the sound speed $c_s$ and drag some of photon-baryon fluid with them, resulting in a sound horizon that would be larger than a neutrinoless universe. Self-interactions slow the speed of the neutrinos, and by tuning the strength of the interaction it is possible to arrange for the CMB spectral peak heights to be unchanged (with some small changes to other parameters such as the primordial power spectrum tilt $n_s$ and $\varOmega _{\varLambda }$). By adding an additional coupling to a new scalar particle, their mixing may be suppressed at BBN, in which case they evade the He abundance constraints. Kreisch et al. (2020) have analysed such a model and found $H_0 = 72.3 \pm 1.4\; \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ for $N_{\mathrm{eff}} = 4.02 \pm 0.29$.

The drawback is the self-interaction must be extremely strong. That is, the effective coupling $G_{\mathrm{eff}}$ required between neutrinos is $\sim 10^{10} G_{\mathrm{Fermi}}$ where the Fermi constant of weak interactions in the Standard Model is $G_{\mathrm{Fermi}} = 1.17 \times 10^{-5}$ $\hbox {GeV}^{-2}$. Such strength contradicts calculations of the decay time of muons and tau leptons, unless the self-interactions are restricted to the tau neutrino, or weakened to a level where they do not fully resolve the tension (Das and Ghosh 2021). So this proposal does seem highly fine-tuned. However, it is accessible to testing by CMB S4 experiments, as it predicts a stronger decrease of the damping tail for modes $\ell > 2000$.

4.2.2 Early dark energy

Early dark energy (EDE) refers to a boost to the expansion of the pre-recombination universe caused by a scalar field potential $V(\phi ) \sim \phi ^n$ in a manner similar to (but milder than) inflation. This dark energy must be present at around $z \sim 10^4$, as that is the time from which most of the growth of the sound horizon occurs. BBN constraints mean it must be absent earlier. The dark energy must also decay by the time of recombination, not to disrupt the damping tail of the CMB spectrum. EDE then provides a short-term boost to the expansion speed, which decreases the sound horizon by modifying the numerator of Eq. (52).

Agrawal et al. (2019) have shown $H_0 \sim 72 \;\;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ for a fraction $\varOmega _{\mathrm{EDE}} \sim 5\%$ of the energy content and the onset of its decay at redshift $z_c \sim 5000$, for a range of potentials. It may be said that this feels like fine-tuning again (though it should be said that the same point may be made about late dark energy—the “why now” problem)! The model shows a small residual oscillatory signal in the CMB spectrum versus a standard ${\varLambda} {\text{CDM}}$ fit, so if $H_0$ is calculated in ${\varLambda} {\text{CDM}}$ in an EDE universe, it is progressively biased lower for higher angular resolution (Knox and Millea 2020). Although this trend is already seen in WMAP and Planck, it is opposite to the trend in SPT.

EDE can then be tested by higher resolution in CMB S4 experiments. It may also be testable before then: it is necessarily present around the time of matter-radiation equality, and, therefore, will leave an imprint in the present-day matter power spectrum P(k). The spectrum captures the strength of matter density fluctuations of wavenumber k and decreases for $k>k_{\mathrm{eq}}$, the wavelength corresponding to matter-radiation equality, with a gradient weakly proportional to $k_{\mathrm{eq}}$. This spectrum is measured in galaxy surveys, and the greater precision of the Vera Rubin Observatory LSST and Euclid survey will constrain the presence of any additional components of the universe at $z_{\mathrm{eq}}$ when EDE needs to be close to its maximum effect.

4.2.3 $T_0$ tension

In Eq. (52), $\omega _r$ is determined by the temperature of today’s CMB, measured by the COBE instrument FIRAS in 1996 to be $T_0 = 2.726 \pm 0.0013 K$ (Fixsen 2009) and the equation of state for radiation energy $T(t) = T_0 (1+z(t))^4$. Changes to $\omega _r$ in (52) can be reabsorbed into changes to h, so there is some degeneracy between the temperature of universe and $H_0$. A thought experiment can then be done: what if $T_0$ was allowed to vary outside FIRAS bounds, keeping other quantities fixed? Ivanov et al. (2020) have considered this, opting to keep fixed $\omega _i / T_0^3$, which corresponds to the absolute energy scale of components. On combining Planck data with SH0ES, they find the $H_0$ tension is resolved within in ${\varLambda} {\text{CDM}}$, but with $T_0 = 2.582 \pm 0.033$.

While this is not new physics unless one proposes a new equation of state for radiation, it is a helpful recasting of the tension. First, no balloon or other measurement of $T_0$ has produced such a low $T_0$ value (Fixsen 2009). Second, the temperature of the universe may be estimated at earlier epochs via the Sunyaev–Zel’dovich effect, providing an independent probe of T(z). Luzzi et al. (2015) use the Planck SZ cluster catalog to find that deviations from $T(z) = T_0 (1+z)$ are limited to $\sim 3\%$ at $2 \sigma$ confidence out to $z = 0.94$.

5 Conclusions and buyer’s advice

Much effort has been expended by all the teams involved to reduce photometric biases, environmental effects, calibration error, lens mass modelling biases, CMB foreground effects and so on. Nevertheless, there remain some areas where a degree of healthy scientific scepticism might be focused, or improvements might be forthcoming. In the spirit of our Buyer’s Guide, we offer our view on these areas in Fig. 18.

Fig. 18

A ‘traffic light’ colour coding corresponding to our view of the calculation of $H_0$ has uncertainties that may improve over the next few years. Green corresponds to a solid current position with low uncertainty, yellow is where some improvements can be expected, and red is where caution or cross-checks may be needed. For more detail the reader may consult the relevant subsection in Sect. 3. This diagram was inspired by a similar plot by Wendy Freedman at the ESO $H_0$ 2020 conference

The last 20 years have seen the error bars on $H_0$ shrink from 8% to 1%–2% for the highest precision results.¹⁸ For the late universe, the SH0ES team has calibrated the Cepheid luminosity zero point to 1.0% precision, and the values are consistent whether parallaxes, the DEB distance to the LMC, or the maser distance to NGC4258 are used. The calibration of SN Ia luminosity adds another 1.3% uncertainty, resulting in $H_0$ to 1.8% accuracy (Riess et al. 2021). For the early universe, the high resolution and sky coverage of Planck results in 0.75% accuracy (Planck Collaboration 2020). This has been characterised as “early versus late” tension, but this would be to ignore the results from the CCHP calibration of TRGBs which are a late universe result intermediate between Planck and SH0ES (Freedman et al. 2019). Additionally, the size of the BAO sound horizon in the late universe when calibrated with early universe BBN constraints is consistent with the CMB value (Addison et al. 2018).

5.1 Systematics or beyond ${\varLambda} {\text{CDM}}$?

Not too surprisingly there is at present no clear answer yet to the question “What is the true value of $H_0$?”. We do, however, think there is a compelling cosmological model, and that is ${\varLambda} {\text{CDM}}$. It has been the best model around for the last 30 years, and no new model has yet presented a convincing case to replace it. Having said that, it is still disturbing that the two main ingredients in ${\varLambda} {\text{CDM}}$, dark matter and dark energy, are not understood. The $H_0$ derived from the CMB is, therefore, part of a “package deal” which involves other cosmological parameters within the ${\varLambda} {\text{CDM}}$ paradigm. Fortunately, the underlying physics of the CMB is well defined—the CMB fluctuation spectrum is a solution of Boltzmann’s equation. In contrast, the cosmic ladder measurements of $H_0$ probe directly this parameter and no others, and the astrophysics of the standard candles used is not fully understood.

Although many plausible extensions of ${\varLambda} {\text{CDM}}$ can resolve the tension, none enjoy majority support. They either do not resolve other tensions related to $H_0$ such as the sound horizon, or seem somewhat contrived. Thus, at best they can be seen as effective theories of some unknown, and possibly more natural, microphysics. Given the lack of a compelling explanation from theory, and a greater understanding of how hard it is to “break” ${\varLambda} {\text{CDM}}$, opinion in the community seems to be shifting. At a conference called “Beyond ${\varLambda} {\text{CDM}}$” in Oslo in 2015, a poll suggested 69% of participants believed new physics the most likely explanation (although we suspect some bias in the voter views given the title of the conference!). However, at a conference in 2021 entitled “Hubble Tension Headache” held virtually by Southampton University, UK, over 50% of participants favoured the explanation that there were still systematics in the data.

5.2 Open issues

Here we comment on some frequently asked questions:

• Is SH0ES $H_0$ supported? Results from Miras, Megamasers and HST Key Project have central values that are consistent with SH0ES, but due to their larger error bars are only in tension with Planck at the $1.5 \sim 3.0 \sigma$ level. Results from lensed quasars, TRGBs and surface brightness fluctuations vary between papers, and cannot be regarded as convincingly supportive of SH0ES.

• Is Planck $H_0$ supported? The Planck value for $H_0$ is corroborated by the Atacama Cosmology Telescope to within 1%, and is also consistent with the earlier WMAP satellite. However, it is in $2.1 \sigma$ tension with the South Pole Telescope. Planck’s $H_0$ is also supported by BAO from the BOSS and DES galaxy surveys combined with an early universe prior for the baryon density.

• Are systematics still present? Regarding Cepheids, considerable recent progress has been made in demonstrating crowding is under control and photometric reduction is free from bias. Nevertheless, potential weaknesses remain in the calibration and environmental corrections of SN Ia, and the calibration of TRGBs has been disputed. Re-analyses of lensed quasars show systematics are not yet under control. The nature of CMB analyses do not lend themselves easily to part-by-part decomposition or independent review, but a full re-analysis of Planck by Efstathiou and Gratton (2019) did not alter cosmological parameters.

• Is characterisation of “early versus late” helpful? The strongest evidence in favour of this are the Cepheid results and Planck, as while other results are broadly consistent with this view they are individually more uncertain. However, if the calibration of TRGB were resolved in favour of the CCHP value, it would weaken the case for this view. It is, however, helpful to consider new cosmological models in terms of those modifying the post- or pre-recombination universe, as at present those modifying the pre-recombination universe appear more viable.

• Is there a convincing theoretical solution? Simply put, ${\varLambda} {\text{CDM}}$ is very hard to break. Proposals need to clear three main hurdles: fitting a wide range of cosmological data, consistency with other predictions of ${\varLambda} {\text{CDM}}$, and providing a convincing Bayesian argument that the model is preferable to ${\varLambda} {\text{CDM}}$. None yet do so. Nevertheless, there are strong hints what a solution might look like, and it is fair to point out that the innovation of $\varLambda$ in ${\varLambda} {\text{CDM}}$ itself solved a previous tension between a low matter density and flat universe.

• Are TRGBs and gravitational waves offering a way forwards? It is likely that a consensus on TRGB calibration will be reached in the near-future, and TRGBs promise cleaner fields and better theoretical modelling than Cepheids. They are also ideal for JWST observations, which has four times the J band resolution of the HST/WFC3 H band. Miras are interesting, but are more expensive to observe and harder to calibrate. Gravitational waves offer an inherently transparent and accurate way to measure $H_0$, once enough bright and dark siren data have been collected by the middle of this decade. If these two were to corroborate SH0ES, it would be strong evidence in favour of the breakdown of ${\varLambda} {\text{CDM}}$. Alternatively, if they agree with Planck, one would have to conclude SH0ES is the outlier.

5.3 Buyer’s advice

We would suggest the following in response to the question of “Which $H_0$ should I use?”, depending on the desired application.

• For cosmological inference: As the tension in the Hubble parameter is between local direct estimates, and the best-fitted ${\varLambda} {\text{CDM}}$ model, the only two possible explanations are unknown systematic effects in the local direct estimate, or that our universe is described by a model different from ${\varLambda} {\text{CDM}}$. If it turns out that there are systematics in the local estimate, it is clear that we should use Planck’s value $H_0 = 67.4 \;\;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Planck Collaboration 2020). If the universe is not ${\varLambda} {\text{CDM}}$, it remains the case that ${\varLambda} {\text{CDM}}$ is a great fit to cosmological data with all other parameters consistent with their CMB-derived values. We, therefore, recommend the full package of Planck or Planck-like cosmological parameters should be used, so one can test the the ${\varLambda} {\text{CDM}}$ model self consistently. A specific example is in choosing parameters for N-body simulations. It makes sense to select the Planck set of parameters ($H_0$, $\varOmega _m$ and $\sigma _8$, etc.) so one can test the growth of structure with cosmic time given ${\varLambda} {\text{CDM}}$ fit to Planck. In contrast, the ${\varLambda} {\text{CDM}}$ model with $H_0 = 73.2 \;\;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ is a poor fit to most existing cosmological observations (CMB and galaxy surveys).

  Another application of using $H_0$ and other parameters from Planck is when using them as priors for analyses of new data sets, in a Bayesian framework. Here the errors bars of parameters or the full Planck posterior of the probability distribution are important, as they propagate through the parameter marginalisation process. We also maintain that it is not correct to inflate $H_0$ confidence intervals to “hedge bets”, unless one does that in a non-${\varLambda} {\text{CDM}}$ model and fully rederives the posteriors for all other parameters in a Bayesian fashion.

• For the local universe:. The SH0ES value of $H_0 = 73.2 \pm 1.3 \; \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Riess et al. 2021) using Gaia parallaxes and Cepheids is a good choice, as it is consistent with independent measurements such as Megamasers and Miras and re-analyses of the data (albeit generally starting with the photometric parameters, and not the original imaging) have produced mostly consistent results. Therefore, the SH0ES value should be used for calculations that require an expansion rate or distances alone, but are local enough to have minimal cosmological model dependence. Having said that, the CCHP TRGB result of $H_0 = 69.8 \pm 1.9 \; \;\,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$ (Freedman et al. 2019) is noteworthy for its consistency with Planck and the advantages TRGB observations may offer relative to Cepheids. It is very much a case of “watch this space” for developments.

• For pedagogical purposes: For the purpose of teaching cosmology, popular talks, or back-of-the-envelope calculations it would make sense to use the intermediate round value of $H_0 = 70 \; \,\hbox {kms}^{-1} \,\hbox {Mpc}^{-1}$. Wherever possible we recommend indicating the dependence of your key results on $H_0$ either in formulae, or as a method to adjust the key results. Anticipating a future resolution of the tension, this will be of great assistance to future researchers.

5.4 Future prospects

Looking to the future, the Zwicky Transient Facility and Foundation surveys of nearby SN Ia will be very helpful in reducing potential calibration issues. They will do this by resolving the underlying population characteristics, having cleaner selection functions, and providing more galaxies in which to calibrate the distant Hubble flow sample. The early signs of Gaia Early Data Release 3 is that it provides a considerable reduction, but not elimination, of the bias apparent in Data Release 2. But it is not the last word, and the next release is scheduled for 2022. The key point of Gaia is that it addresses lingering concerns about how the low metallicity environment of the LMC, or the maser disk modelling and crowded fields of NGC4258 may affect the calibration of standard candles. In particular, it will be useful to have accurate Gaia parallaxes to Milky Way globular clusters such as $\omega$Cen to provide additional calibrators of the TRGB. The JWST will greatly expand the range of TRGB observation, and provide continuity in the case of any further degradation of the ageing HST. The Extremely Large Telescope in Chile, scheduled for first light in 2025, can extend the range of DEB distances to M31 allowing it to contribute its Cepheid and TRGB populations to calibrations.

In the field of gravitational waves, it is perhaps disappointing that there have been no more observations of “bright sirens” like the neutron star merger GW170817 so far. But the commencement of operations at the VIRGO detector in Italy, and recently the KAGRA detector in Japan offer hope that the more frequent event detections and better sky localization, combined with an improved instrumental calibration, will provide a 2% measurement of $H_0$ within this decade. Many more time-delay lensing systems will be seen in future galaxy surveys, so there is a strong incentive to resolve remaining systematics in the modelling and speed up the analysis pipeline.

The Simons Telescope in Chile aims to map the polarisation spectrum of the CMB to an order of magnitude higher than Planck, and will start taking data in the next two to three years. Close to 2030, two new CMB Stage 4 telescopes will be operational in Chile and the South Pole, which will further extend the spectral resolution. The depth of these surveys will be able to support or rule out many pre-combination modifications of ${\varLambda} {\text{CDM}}$. Surveys conducted by the Dark Energy Spectroscopic Instrument (DESI), Vera C. Rubin Observatory (previously named LSST), Euclid satellite and Nancy Grace Roman Space Telescope (previously named WFIRST), combined with theoretical progress in the quasi-linear regime of structure formation, will enable the matter-power spectrum to be compared with ${\varLambda} {\text{CDM}}$ predictions with much greater depth and resolution.